用matlab的编程法和游动鼠标法求二阶传递函数的上升时间、峰值时间、超调量和调节时间 - Gavin_Hall的博客 - CSDN博客

178 阅读 0 评论 118 点赞

我是靠谱客的博主长情太阳，最近开发中收集的这篇文章主要介绍用matlab的编程法和游动鼠标法求二阶传递函数的上升时间、峰值时间、超调量和调节时间 - Gavin_Hall的博客 - CSDN博客，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 准备

终值：c(∞)
上升时间 t_r：响应从峰值的10%上升到峰值的90%所需要的时间；而阶跃响应则是从终值的10%上升到终值的90%所需要的时间；对有振荡的系统，也可以定义为从0到第一次到达终值所需的时间。
峰值时间 t_p：响应到达第一个峰值所需的时间。
调节时间 t_s：响应到达并保持在终值的正负5%误差带内所需的最短时间；有时也用终值的正负2%。
超调量 σ%：峰值c(t_p )超出终值的百分比，即：
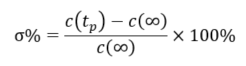
在这里插入图片描述

题目：

已知二阶系统传递函数为
在这里插入图片描述
试分别用游动鼠标法和编程法求取系统的峰值，超调量，上升时间以及调节时间。

2. 编程法：

s = tf('s');   % 用字母 s 构造传递函数
Gs = 3/(s^2+2*s+10); % 构造 Gs
t = 0:0.005:5; % 设置横轴范围和步长
[y,x,t] = step(Gs,t); % 根据步长逐步响应传递函数
[ymax,tp] = max(y); % 获取最大值的点的数据

r=1;
r1=0;
while y(r) < (ymax*0.9) % 过滤小于90%的
    if y(r) > (ymax*0.1) % 过滤大于10%的
        r1=r1+1;
    end;
    r=r+1;
end;

rise_time = r1*0.005 % 上升时间
peak_time = (tp-1)*0.005 % 峰值时间
ystable = dcgain(Gs); % 稳态值
max_overshoot = (ymax-ystable)/ystable % 超调量

r2=1001; % 由 (5-0)/0.005+1 求得
while y(r2) > ystable*0.98 && y(r2) < ystable*1.02 
    % 从稳态倒推回去，求得首次达到并维持在稳态值正负2%的范围的值
    r2 = r2 - 1;
end
settle_time = (r2-1)*0.005 % 调节时间

求得：

rise_time =   0.6100
peak_time = 1.0450
max_overshoot = 0.3509
settle_time = 3.5350

3. 游动鼠标法：

游动鼠标法不适合用于plot()命令画出的图形，只能在非plot()函数输出的曲线上求取。
1.获取必要数据

s = tf('s');
Gs = 3/(s^2+2*s+10); % 构造 Gs
t = 0:0.005:5;
step(Gs,t)  % 画出图像
[y,x,t] = step(Gs,t); 
[ymax,tp] = max(y); 
ymax	% 峰值
ym10 = ymax * 0.1  % 峰值 10%
ym90 = ymax * 0.9  % 峰值 90%
ystable = dcgain(Gs) % 稳态值
ys98 = ystable * 0.98  % 稳态 -2%
ys102 = ystable * 1.02   %  稳态 +2%

得到图像并求得：

ymax = 0.4053
ym10 = 0.0405
ym90 = 0.3647
ystable = 0.3000
ys98 = 0.2940
ys102 = 0.3060

2.点击工具栏中的数据游标，在图中分别标出纵坐标为 ymax = 0.4053，ym10 = 0.0405，ym90 = 0.3647，ys98 = 0.2940，ys102 = 0.3060 的五点：
在这里插入图片描述

3.收集图像中 Time 对应的 Amplitude 数据，并计算可得：
t_r = 0.783 - 0.176 = 0.607
t_p = 1.04
t_s = 3.53 (因为0.295位于此波谷最低处，而0.295>0.294，故不取4.19)
σ% = (0.405 - 0.3)/0.3 × 100% = 35%