前段时间尝试了C语言实现PSO算法求计算二元函数极值,这几天稍微空闲下来了又想尝试用另一种比PSO难一点的经典智能优化算法解决这个问题。
PSO传送门
遗传算法应用还是非常广泛的。之前打数模的时候经常用它求解公式,或者利用它做一些调度类的问题,例如经典的柔性车间调度问题。但是,在实现的时候更多的是借助matlab和python,有的时候直接拿现成的代码修改参数直接用,对算法的理解还是很不到位的。趁这个机会,打算用C语言实现一次GA算法。
自制的GA算法流程图如下,和PSO算法一样,个人认为这类算法还是静下心来直接看代码比较好理解,效率更高。
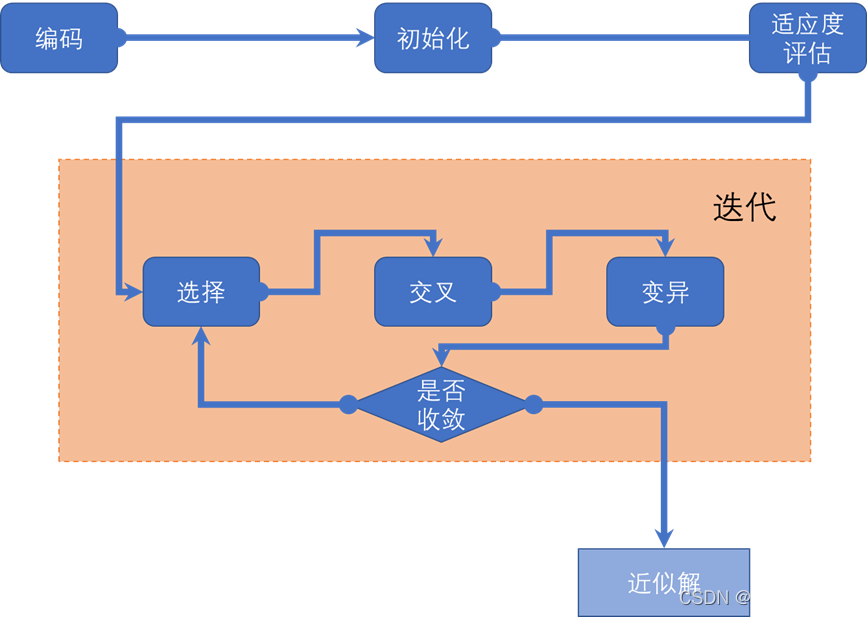
整个算法实际上分为两大部分,第一部分是在为后来的迭代做准备,包括数据编码,初始化等等操作,为第二部分的迭代准备原材料。第二部分是迭代,实际上就是不断地加工第一部分提供的原材料,直到收敛得到最优结果。
实例
待求极值函数如下: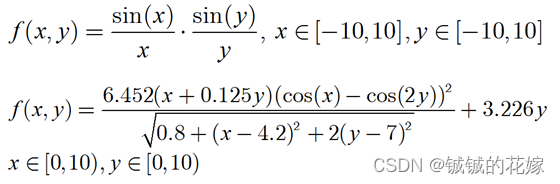
C语言代码如下,主要的流程在genetic函数里写的比较清楚;两个题目可以在fitting函数里面切换,修改的时候记得改#define里的最大最小值。里面的参数需要根据题目自己调整。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207#include<bits/stdc++.h> using namespace std; // 染色体数量 也就是种群数量 #define chromosome_size 300 // 染色体长度 也就是维度 #define chromosome_length 2 // 进化代数 也就是迭代次数 #define epoch_max 30 // 变量上下界 #define bound_down 0 #define bound_up 10 // 交叉概率 #define cross_probability 0.5 // 变异概率 => 模仿生物学,这玩意要低 #define mutation_probability 0.1 // 染色题本身 二维就是这个解的x,y存储 double chromosome[chromosome_size][chromosome_length]; // 染色体适应度函数 二维就是这个解的x,y对应的函数的值的存储 double chromosome_fitness[chromosome_size]; // 个体被选中的概率,这个是遗传算法的特色 double chromosome_chosen[chromosome_size]; // 每次迭代的最优解 double epoch_best_fitness[epoch_max]; // 每次迭代的最优解的位置,在二维里就是对应的x, y double epoch_best[epoch_max]; // 之前所有迭代的最优解的平均值 double average_epoch_best_fitness[epoch_max]; // 存储目前所有迭代中的最优解 double all_best_fitness; // 存储目前所有迭代中的最优解出现的代数 int all_best_epoch; // 求和函数,因为不让用库,只能手写一个 double sum(double fit[]) { double sum_fit = 0; for(int i=0;i<chromosome_length;i++) sum_fit += fit[i]; return sum_fit; } // 计算适应度的函数,在二维的情况下其实就是计算x, y这俩对应的函数的解 double fitting(double fit[]){ // 第一题: // double fitness = sin(fit[0])/fit[0]+sin(fit[1])/fit[1]; // 第二题 double fitness = (6.452*(fit[0]+0.125*fit[1])*pow((cos(fit[0])-cos(2*fit[1])),2))/sqrt(0.8+pow((fit[0]-4.2),2)+2*pow((fit[1]-7),2))+3.226*fit[1]; return fitness; } // 作用其实就是比较所有散点对应的适应度,输出最大的适应度和对应的位置 double* max_in_community(double fit[], int size){ static double result[2]; result[0] = *fit; result[1] = 0; for(int i = 0; i < size; i++) if(fit[i]>result[0]){ result[0] = fit[i]; result[1] = i; }; return result; } // 初始化函数,一开始还是随机初始化 void initialization(void){ for(int i = 0; i < chromosome_size; i++){ for(int j = 0; j < chromosome_length; j++) // 初始化第一代 chromosome[i][j] = bound_up*(((double)rand())/RAND_MAX)+bound_down; // 顺便算出来第一批染色体的适应度函数 chromosome_fitness[i] = fitting(chromosome[i]); } } // 选择:求最大值时,适应度越高,被选择的概率越大,经过选择之后,chromosome中大的比例明显提高了 void select(double chromosome[chromosome_size][chromosome_length]){ double fitness_sum = 0; for(int i=0; i<chromosome_size; i++){ // 计算适应度 chromosome_fitness[i] = fitting(chromosome[i]); // 求和,为了之后能算概率 fitness_sum += chromosome_fitness[i]; } // 计算每个染色体的概率 for(int i=0; i<chromosome_size; i++){ if(i==0) chromosome_chosen[i] = chromosome_fitness[i]/fitness_sum; else chromosome_chosen[i] = chromosome_fitness[i]/fitness_sum+chromosome_chosen[i-1]; } // 选择的主体 => 随机数筛选,染色体的概率越大,越容易被select到 int index[chromosome_size]; for(int i=0; i<chromosome_size; i++){ double rand0 = ((double)rand())/RAND_MAX; while(rand0<0.0001) rand0 = ((double)rand())/RAND_MAX; for(int j=0; j<chromosome_size; j++){ if(rand0<=chromosome_chosen[j]){ index[i] = j; break; } } } // 选择完了,在这里记录 for(int i=0;i<chromosome_size;i++){ for(int j=0;j<chromosome_length;j++) chromosome[i][j]=chromosome[index[i]][j]; chromosome_fitness[i] = chromosome_fitness[index[i]]; } } // 交叉 void cross(double chromosome[chromosome_size][chromosome_length]){ for(int i=0;i<chromosome_size;i++){ // 上来先判断是否进行交叉操作,大于交叉概率就跳过 double pick = ((double)rand())/RAND_MAX; if(pick>cross_probability) continue; // 交叉涉及到两个染色体,在这里随机抽取两个染色体,下面两个是两个染色体的编号 int rand1 = (int)((chromosome_size-1)*((double)rand())/RAND_MAX); int rand2 = (int)((chromosome_size-1)*((double)rand())/RAND_MAX); // 交叉主体 int flag = 0; // 用来判断后面的循环是否要退出的 while(!flag){ // 看染色体的哪部分拿过来交叉互换 int where = (int)((chromosome_length-1)*((double)rand())/RAND_MAX); double v1 = chromosome[rand1][where]; double v2 = chromosome[rand2][where]; // rand是指交叉时采用交叉对象的比例 double rand0 = ((double)rand())/RAND_MAX; chromosome[rand1][where] = rand0*v2 + (1-rand0)*v1; chromosome[rand2][where] = rand0*v2 + (1-rand0)*v2; // 判定上下界,在界内就算这次交叉算数,不然重新交叉 if(chromosome[rand1][where]<=bound_up&&chromosome[rand1][where]>=bound_down) if(chromosome[rand2][where]<=bound_up&&chromosome[rand2][where]>=bound_down) flag = 1; } } } // 变异 void mutation(double chromosomes[chromosome_size][chromosome_length]) { for(int i=0;i<chromosome_size;i++){ // 上来先判断是否进行变异操作,大于变异概率就跳过 double pick = ((double)rand())/RAND_MAX; if(pick>mutation_probability) continue; // 随机抽取染色体的一个位置 int where = (int)((chromosome_length-1)*((double)rand())/RAND_MAX); double v1 = chromosome[i][where] - bound_up; double v2 = bound_down - chromosome[i][where]; double r = ((double)rand())/RAND_MAX; double r1 = ((double)rand())/RAND_MAX; if(r>=0.5) chromosome[i][where] = chromosome[i][where] - v1*r1*(1-((double)i)/epoch_max)*(1-((double)i)/epoch_max); else chromosome[i][where] = chromosome[i][where] + v1*r1*(1-((double)i)/epoch_max)*(1-((double)i)/epoch_max); } } // 遗传搜索 void genetic(){ //————————————Step1————————————// //——————————各种初始化——————————// // 初始化染色体 initialization(); // 该轮所有染色体适应度的最大值和index double *best_fitness_index; best_fitness_index = max_in_community(chromosome_fitness, chromosome_size); // 初始化平均值 average_epoch_best_fitness[0] = sum(chromosome_fitness)/chromosome_size; // 初始化每代最佳染色体与适应度对应的适应度 all_best_fitness = best_fitness_index[0]; all_best_epoch = 0; for(int i = 0; i < chromosome_length; i++) epoch_best[i] = chromosome[(int)best_fitness_index[1]][i]; //————————————Step2————————————// //————————————迭代————————————// for(int i=0; i<epoch_max; i++){ // 选择交叉变异一套搞定 select(chromosome); cross(chromosome); mutation(chromosome); //更新一系列数据 // 计算操作后染色体对应的适应度 for(int j=0; j<chromosome_size; j++) chromosome_fitness[j] = fitting(chromosome[j]); // 计算平均值 average_epoch_best_fitness[i+1] = sum(chromosome_fitness)/chromosome_size; // 储存最优表现 best_fitness_index = max_in_community(chromosome_fitness, chromosome_size); if(best_fitness_index[0] > all_best_fitness){ all_best_fitness = best_fitness_index[0]; for(int k=0; k<chromosome_length; k++) epoch_best[k] = chromosome[(int)best_fitness_index[1]][k]; all_best_epoch = i+1; } printf("第%d次迭代:(%lf,%lf)t%lfn", i, chromosome[(int)best_fitness_index[1]][0], chromosome[(int)best_fitness_index[1]][1], best_fitness_index[0]); } } int main(){ //程序开始和结束时间 clock_t begin, end; begin = clock(); //开始计时 srand((unsigned)time(NULL)); // 初始化随机数种子 // 搜索 genetic(); end = clock(); printf("计算总耗时:%lf秒n", ((double)(end-begin))/CLOCKS_PER_SEC); printf("遗传算法进化了%d次,最优值为:%lf,最优值在第%d代取得,此代的平均最优值为%lf.n",epoch_max,all_best_fitness,all_best_epoch,average_epoch_best_fitness[all_best_epoch]); printf("取得最优值的地方为(%lf,%lf).n",epoch_best[0],epoch_best[1]); return 0; }
不是很确定最后的结果对不对,拿matlab试试结果。先浅浅画俩图:
1
2
3fsurf(@(x,y)sin(x)/x+sin(y)/y) fsurf(@(x,y)(6.452*(x+0.125*y)*(cos(x)-cos(2*y))^2/(0.8+(x-4.2)^2+2*(y-7)^2)^(1/2))+3.226*y)
例题1:
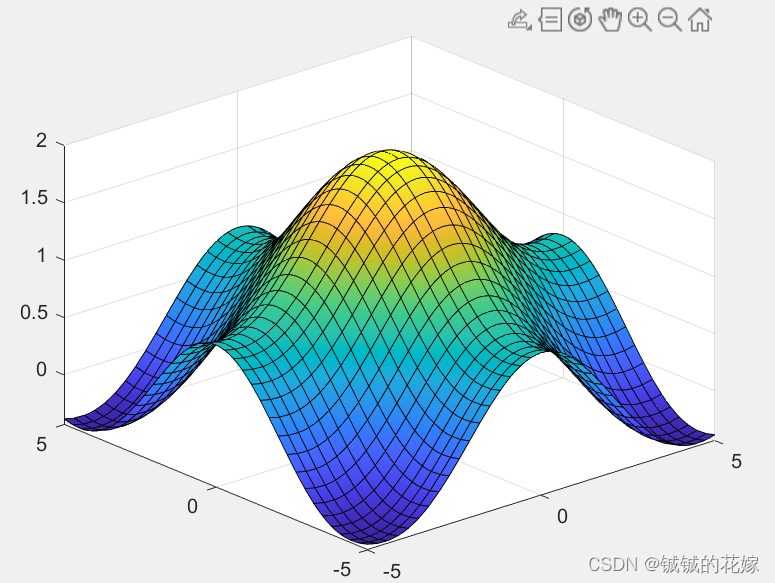
例题2:
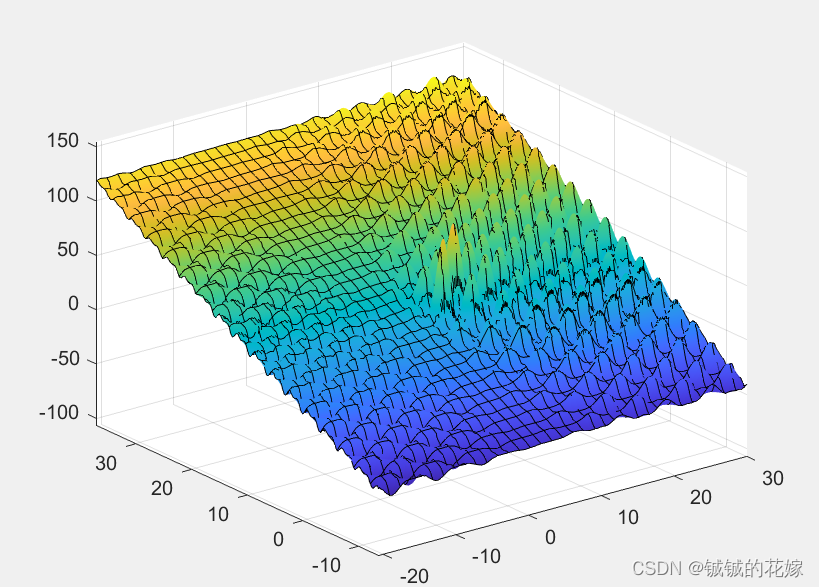
matlab自带PSO求解工具计算极值,因为这个东西只能算最小值,所以对原函数取负号,得到的最小值再取负就是我们要的最大值:
1
2
3[x,fval] = ga(@(x)-(sin(x(1))/x(1)+sin(x(2))/x(2)),2,[],[],[],[],[-10,-10],[10,10], [], gaoptimset('CrossoverFraction', 0.6)) [x,fval] = ga(@(x)-(6.452*(x(1)+0.125*x(2))*(cos(x(1))-cos(2*x(2)))^2/(0.8+(x(1)-4.2)^2+2*(x(2)-7)^2)^(1/2)+3.226*x(2)),2,[],[],[],[],[0,0],[10,10], [], gaoptimset('CrossoverFraction', 0.6))
运行结果如下:


经过证明,我们C语言的实现是没什么大问题的。
最后
以上就是沉静老鼠最近收集整理的关于遗传算法(GA)计算二元函数极值(C语言实现、matlab工具箱实现)实例的全部内容,更多相关遗传算法(GA)计算二元函数极值(C语言实现、matlab工具箱实现)实例内容请搜索靠谱客的其他文章。








发表评论 取消回复