我是靠谱客的博主 明亮小笼包，这篇文章主要介绍matlab_迭代学习控制_论文例子1_开环 三种方法方法一、利用simulink的 from to workspace方法二、给定传函转为状态方程方法三、 给定传函转为差分方程，现在分享给大家，希望可以做个参考。
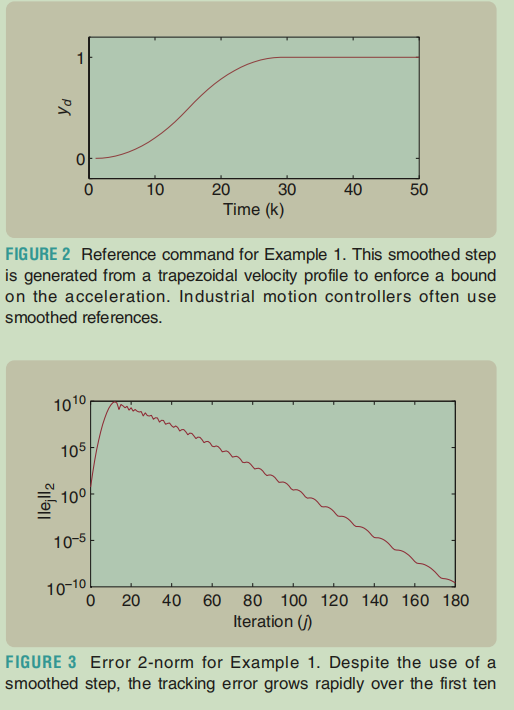
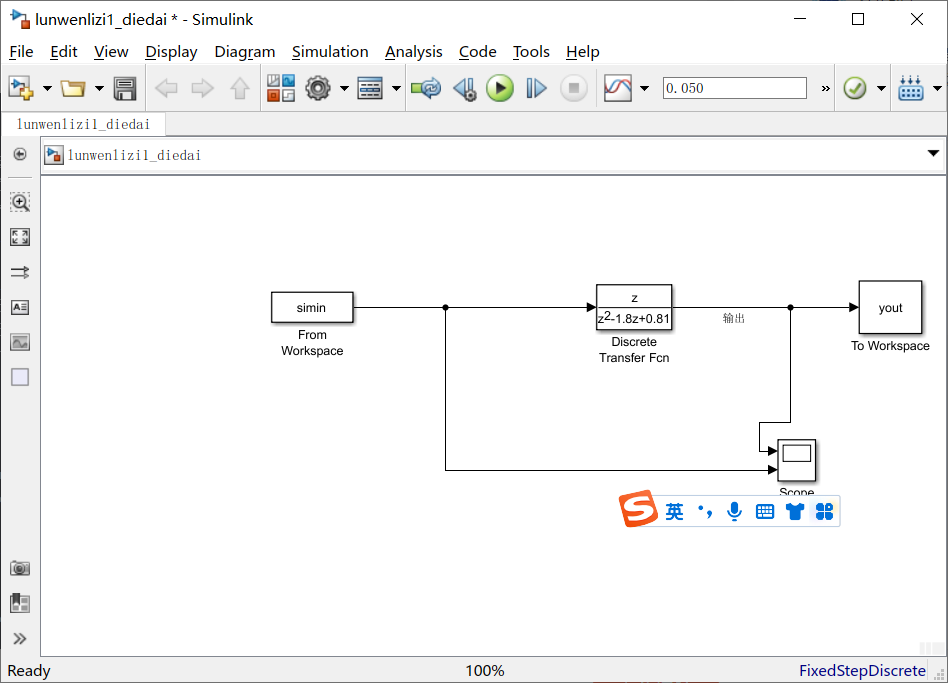
方法一、利用simulink的 from to workspace
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39clc; clear; K=50; % 每次迭代的时间 J=180; %总迭代次数 ts=0.001; %采样时间 t=[0:ts:K*ts]';%仿真时间 yd=sin(2*pi*50*t); %跟踪轨迹/期望输出 u(1:0.050/ts+1,1)=1; %第一次迭代输入 y_all=[]; %记录所有迭代所有时刻输出 e_all=[]; %记录所有迭代的所有时刻误差 u_all=[]; %记录所有迭代所有时刻输入 for j=1:J simin=[t,u]; simout=sim('lunwenlizi1_diedai'); y_all=[y_all,yout]; e=yd-yout; e_all=[e_all,e]; for k=1:K-1 u(k)=u(k)+0.5*e(k+1); %迭代学习函数 end u_all=[u_all,u]; end %绘图观察实验效果 subplot(2,1,1) plot(1:J,log(e_all(15,:))); %第十五时刻误差随迭代的变换 subplot(2,1,2) plot(1:18,y_all(1:18,50),'+'); %第五十次迭代前十八时刻的输出 hold on plot(1:18,yd(1:18));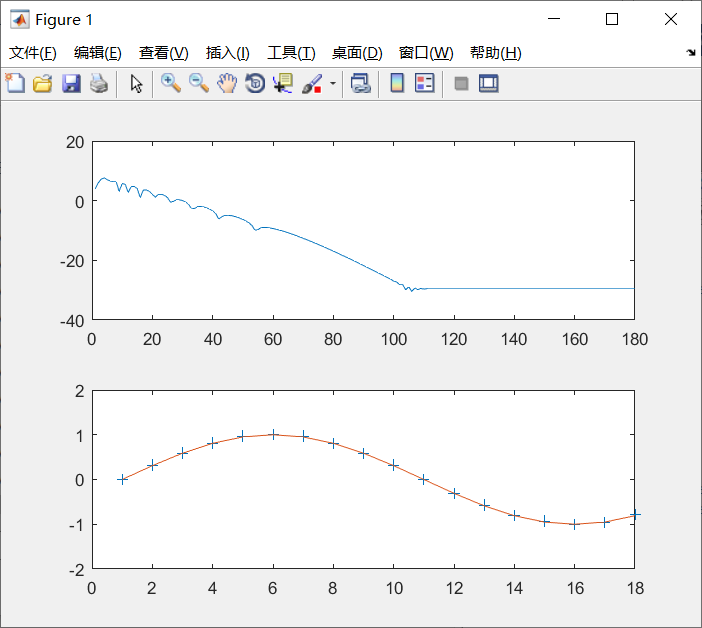
simulink文件：
matlab迭代学习控制论文中的例子三种方法-机器学习文档类资源-CSDN下载
方法二、给定传函转为状态方程
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121%%迭代学习控制论文中的例子一。给定离散传函转为状态方程。 %% P型学习算法 clc; %求离散传函的状态空间表达式 num=[1 0]; den=conv([1 -0.9],[1 -0.9]); P=tf(num,den,1) %离散传递函数，设采样时间为1 [A,B,C,D]=tf2ss(num,den); x1=[]; %两个状态变量 x2=[]; u=[]; e=[]; yd=[]; y=[]; %初始化 T=50; %时间 J=100; %迭代次数 x1(1:J,1)=[0]; x2(1:J,1)=[0]; u(1,1:T+1)=1; yd=[]; lp=0.5; %迭代学习控制渐进稳定判别准则一：q0*(1-l0*p1)=1*（1-0.5*1）=0.5<1 for j = 1:J for k=1:T+1 %状态空间 x = A*[x1(j,k);x2(j,k)]+B*u(j,k); %%!一个式子左边不可以同时赋两个变量 x1(j,k+1)=x(1,:); x2(j,k+1)=x(2,:); y(j,k)=C*[x1(j,k);x2(j,k)]+D*u(j,k); yd(j,k)=1-exp(-k); %跟踪轨迹 end for k=1:T %迭代学习 e(j,k+1)=yd(j,k+1)-y(j,k+1); u(j+1,k)=u(j,k) + lp * e(j,k+1); end end 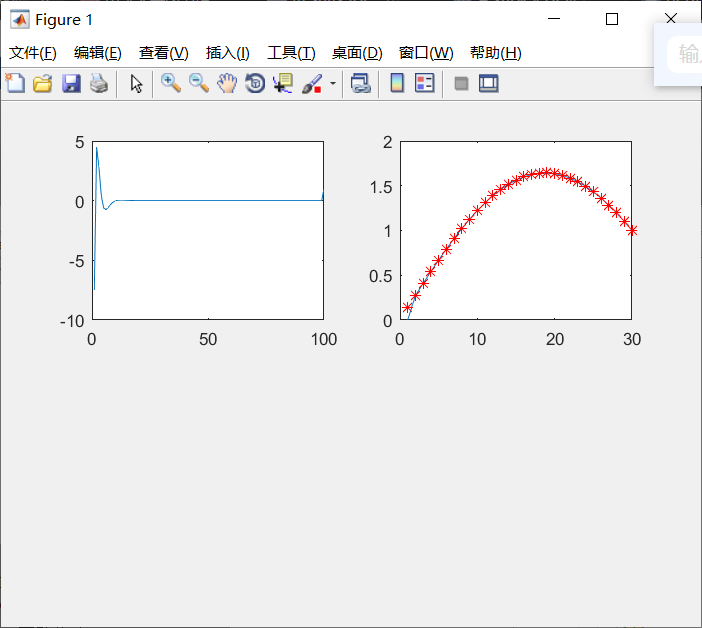subplot(2,2,1) plot(1:J,log10(abs(e(1:J,30)))); %观察第30s误差随迭代次数的变化 xlabel('j');ylabel('abs(e)'); subplot(2,2,2) plot(1:0.6*T,y(80,1:0.6*T)); %观察第80次迭代，前30s内的输出 hold on plot(1:0.6*T,yd(80,1:0.6*T),'r*'); xlabel('k');ylabel('y,yd'); % %%迭代学习控制论文中的例子一 给离散传函转为状态方程 % %% P型 % clc; % N=100; % x1=ones(N,N); %%状态 x是二维的，得设两个变量 % x2=ones(N,N); % u=ones(N,N); % e=ones(N,N); % yd=ones(N,N); % y=ones(N,N); % % A = [0,1; % -0.81,1.8]; % B = [0; % 1]; % C = [0,1]; % D = 0; %%%？？？？？？D若有值就发散了。。。。。 % [num,den]=ss2tf(A,B,C,D) % p1=tf(num,den); % 连续传函 % P2=tf(num,den,1) % 离散传函 p0=0.6 p1=0.51 % % x1(:,1)=[0]; % x2(:,1)=[0]; % u(:,1)=1; % lp=0.5; %迭代学习控制判别准则 q0*(1-l0p1)=1*（1-1.25*0.51）=0.3625 % % % for j = 1:N-1 % for k=1:30 % x = A*[x1(j,k);x2(j,k)]+B*u(j,k); %%!一个式子左边不可以同时赋两个变量 % x1(j,k+1)=x(1,:); % x2(j,k+1)=x(2,:); % y(j,k)=C*[x1(j,k);x2(j,k)]+D*u(j,k); % yd(j,k)=0.5.*sin(0.06.*(k))+1.2.*sin(0.09.*(k)); % end % for k=1:30 % e(j,k+1)=yd(j,k+1)-y(j,k+1); % u(j+1,k)=u(j,k) + lp * e(j,k+1); % end % end % % k=1:30; % subplot(2,2,1) % plot(1:N,e(1:N,5)); % subplot(2,2,2) % plot(k,y(99,1:30)); % hold on % plot(k,yd(99,1:30),'r*');
num =
0 1 0
den =1.0000 -1.8000 0.8100
P2 =
z
------------------
z^2 - 1.8 z + 0.81
Sample time: 1 seconds
Discrete-time transfer function.
方法三、 给定传函转为差分方程
不如转为状态方程
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30% 迭代学习控制 %论文中的例子，系统为离散传递函数，有两个疑问。 %初值 u=ones(181,100); e=ones(181,100); yd=ones(181,100); y=ones(181,100); y(:,1)=1; y(:,2)=2.8;%%？？？？初始值通过传递函数算出来的，为什么差分方程算出来不一致？ % 系统 for j=1:180 for k=1:90 y(j,k+2)=1.8*(y(j,k+1))-0.81*y(j,k)+u(j,k+1); end for k=1:90 e(j,k+1)=yd(j,k+1)-y(j,k+1); u(j+1,k)=u(j,k)+0.5*e(j,k+1); end end j=1:181;k=1:100; subplot(2,2,1) stairs(k,y(30,:)) subplot(2,2,2) stairs(j,log10(e(:,30))) uu=ones(181,100); num=[1,0]; den=[1 -1.8 0.81]; yy=filter(num,den,uu(1,:)); subplot(2,2,3) stairs(k,yy)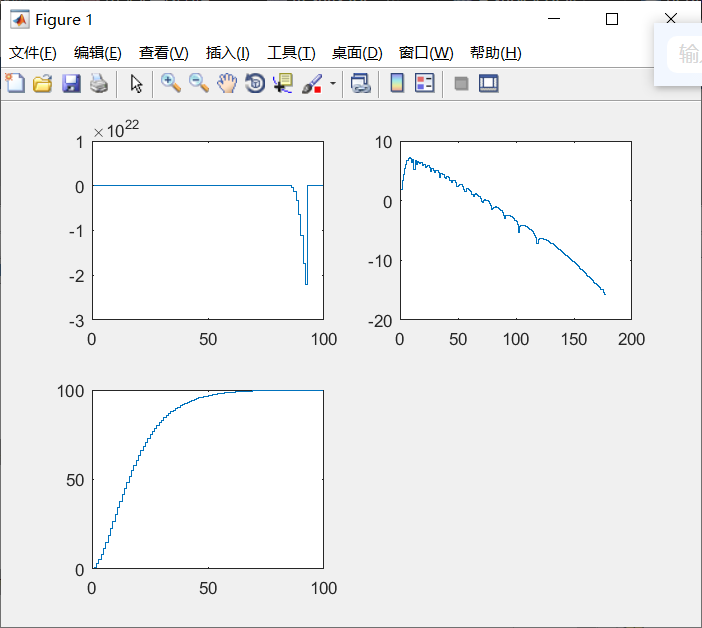
最后
以上就是明亮小笼包最近收集整理的关于matlab_迭代学习控制_论文例子1_开环 三种方法方法一、利用simulink的 from to workspace方法二、给定传函转为状态方程方法三、 给定传函转为差分方程的全部内容，更多相关matlab_迭代学习控制_论文例子1_开环内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复