ode45的常用和扩展用法

写在开头：本文是ode45基础及扩展篇：
1.介绍ode45使用方法、使用技巧；
2.介绍ode45的算法原理，促进理解。

一.简单介绍：

1.先直接引用百度百科上的内容（为了避免重复造轮子）

2.四步-龙格库塔计算方法：

二.ode45使用方法：

由前面的介绍可知ode45主要用于求常微分方程的数值解，它的最基本使用格式为：
[t,y] = ode45(odefun,tspan,y0)
（其中 tspan = [t0 tf]）
求微分方程组 y′=f(t,y)
从 t0 到 tf 的积分，初始条件为 y0。
解数组 y 中的每一行都与列向量 t 中返回的值相对应
简单示例：

1
2
3
4
5
6
7
tspan = [0 5];
% tspan 积分区间
y0 = 0;
% y0 初始值
[t,y] = ode45(@(t,y) 2*t, tspan, y0);
% 求解的微分方程：y'=2*t

对解画图：plot(t,y,'-o');

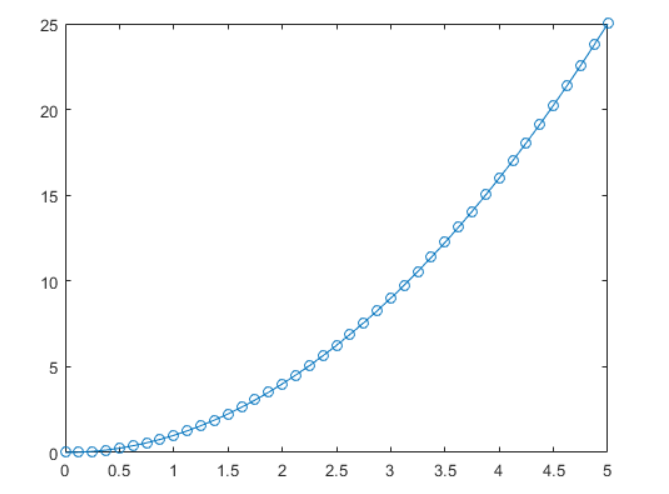
三.一些使用技巧

1. 在实际使用ode45函数过程中，我们经常需要传递一些与自变量t无关的参数，这时我们可采用@（t,y）odefun(t,y,a,b,c…)代替@odefun，或者采用嵌套函数的方法传递参数值。
2. ode45函数求解的常微分方程中若出现二阶导数y‘’，则可看成y‘的导数，从而通过 “多列一个一阶ode方程”的方法求解
3. ode45函数采用的是四步龙格库塔算法，简单点说就是重复：y（x+dt）=y（x）+y’*dt 这一操作（y’的确定正是龙格库塔算法的用武之处）

参考：

ode45介绍-https://ww2.mathworks.cn/help/matlab/ref/ode45.html?s_tid=srchtitle#bu3l43b
0de45百度百科-https://baike.baidu.com/item/ode45/6674723
函数传递额外参数-https://ww2.mathworks.cn/help/optim/ug/passing-extra-parameters.html

最后：资料收集、整理不易，想要转载的小伙伴注明出处就ok哦

最后

以上就是活泼帅哥最近收集整理的关于ode45的常用和扩展用法的全部内容，更多相关ode45内容请搜索靠谱客的其他文章。