hdu 2256 Problem of Precision（矩阵乘法+共轭公式）

Problem Description

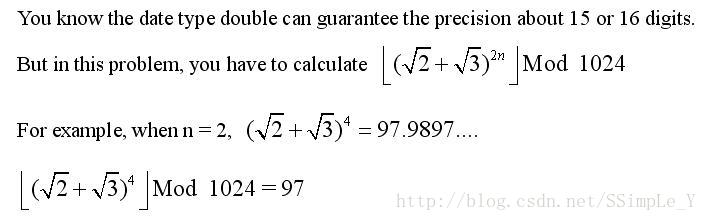
Input
The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9)

Output
For each input case, you should output the answer in one line.

Sample Input
3
1
2
5

Sample Output
9
97
841

Source
HDOJ 2008 Summer Exercise（4）- Buffet Dinner

题目让求$(\sqrt{2}+\sqrt{3}{)}^{2n}$
就是求$(5+2\sqrt{6}{)}^n$

因为出现了根号和向上取整，所以我们可以往凑整数方面想。
$(5+2\sqrt{6}{)}^n=x_n+y_n\ast \sqrt{6}$
$(5-2\sqrt{6}{)}^n=x_n-y_n\ast \sqrt{6}$
因为$(5-2\sqrt{6})<1$ ,所以 $(5-2\sqrt{6}{)}^n<1$
所以$ceil(s_n)=(5+\sqrt{6}{)}^n+(5-\sqrt{6}{)}^n$
又因为$s_n$ 不为整数，所以
所以$floor(s_n)=ceil(s_n)-1$
因为 $ceil(s_n)=2\ast x_{n}n$
所以 $floor(s_n)=2\ast x_n-1$

这样我们只需构造出矩阵求出$x_n$ 就行了

$s_n=s_{n-1}\ast (5+2\sqrt{6})$
$x_n+y_n\ast \sqrt{6}=(5x_{n-1}+12y_{n-1})+(2x_{n-1}+5y_{n-1})\sqrt{6}$

所以矩阵为：
KaTeX parse error: No such environment: smallmatrix at position 14: bigl( begin{̲s̲m̲a̲l̲l̲m̲a̲t̲r̲i̲x̲}̲ x_1 & y_1 \ 0…

$x_1 = 5, y_1 = 2 $

另一篇是 hdu 4565，是向上取整，可以一起看一下。
(http://blog.csdn.net/ssimple_y/article/details/76614336)

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;

int mod = 1024;

struct Matrix
{
    long long m[2][2];
    int n;
    Matrix(int x)
    {
        n = x;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
                m[i][j] = 0;
    }
    Matrix(int _n,int a[2][2])
    {
        n = _n;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
            {
                m[i][j] = a[i][j];
            }
    }
};
Matrix operator *(Matrix a,Matrix b)
{
    int n = a.n;
    Matrix ans = Matrix(n);
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            for(int k=0;k<n;k++)
            {
                ans.m[i][j] += (a.m[i][k]%mod)*(b.m[k][j]%mod)%mod;
                ans.m[i][j] %= mod;
            }
    return ans;
}
Matrix operator ^(Matrix a,int k)
{
    int n = a.n;
    Matrix c(n);
    int i,j;
    for(i=0;i<n;i++)
        for(j=0;j<n;j++)
            c.m[i][j] = (i==j);
    for(;k;k>>=1)
    {
        if(k&1)
            c=c*a;
        a = a*a;
    }
    return c;
}

int main(void)
{
    int T,n;
    scanf("%d",&T);
    int a[2][2] = { 5,2,
                    0,0};
    Matrix A(2,a);
    int b[2][2] = { 5,2,
                    12,5};
    Matrix B(2,b);
    while(T--)
    {
        scanf("%d",&n);
        Matrix ans = A*(B^(n-1));
        printf("%dn",(ans.m[0][0]*2-1)%mod);
    }

    return 0;
}

最后

以上就是默默老鼠最近收集整理的关于hdu 2256 Problem of Precision（矩阵乘法+共轭公式）的全部内容，更多相关hdu内容请搜索靠谱客的其他文章。