Python实现Logistic Regression（逻辑回归模型）算法

       声明：代码的运行环境为Python3。Python3与Python2在一些细节上会有所不同，希望广大读者注意。本博客以代码为主，代码中会有详细的注释。相关文章将会发布在我的个人博客专栏《Python从入门到深度学习》，欢迎大家关注~

       Logistic Regression算法是一个分类算法，分类算法是一种监督学习算法，它是指根据样本的特征，将样本划分到指定的类别中。Logistic Regression是一个二分类的线性分类算法，说到线性分类算法就不得不说一下线性可分与线性不可分的概念了，如果一个分类问题可以使用线性判别函数正确分类，则称该问题为线性可分，否则称为线性不可分问题。

一、模型介绍

1、Sigmoid函数

       Logistic Regression模型属于线性分类模型，对于线性可分问题，我们需要一条直线将不同的类进行区分，这条直线被表示为：

       其中，W为权重值，b为偏置项，这条直线也被称为超平面。在Logistic Regression模型中，学习得到该直线之后，将数据分为两类，可以通过阈值函数将数据映射到不同的类别中，常用的阈值函数有Sigmoid函数，它表示为：

       代码实现Sigmoid函数：

def sigmoid(x):
    '''
    定义sigmoid函数
    :param x: 参数x
    :return: 返回计算后的值
    '''
    return 1.0 / (1 + np.exp(-x))

2、损失函数

       对于Logistic Regression模型来说，权重W和偏置b是唯一的未知参数，故求其值就显得尤为重要！为了求权重和偏置的值，我们需要定义损失函数。

       对于Logistic Regression算法，其属于类别a的概率为：

       其中，是Sigmoid函数。假设有n个样本，我们使用极大似然估计对其进行估计，这里我们使用Log函数，将负的Log似然函数作为其损失函数，于是问题转换为对负的Log函数求极小值，表示为：

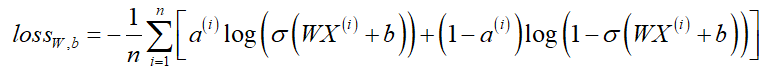
       代码实现求解损失函数：

def errorRate(pre, label):
    '''
    损失函数
    :param pre: 预测值
    :param label: 实际值
    :return: 错误率
    '''
    m = np.shape(pre)[0]
    errSum = 0.0
    for i in range(m):
        if pre[i, 0] > 0 and (1 - pre[i, 0]) > 0:
            errSum -= (label[i, 0] * np.log(pre[i, 0]) + (1 - label[i, 0]) * np.log(1 - pre[i, 0]))
        else:
            errSum -= 0.0
    return errSum / m

二、梯度下降法

       在很多监督学习模型中，都需要对原始模型构建损失函数，接下来通过优化算法对损失函数进行优化，找到最优的解，优化算法中常用的例如最小二乘法、梯度下降法等等。此处，为了求得损失函数的最优解，我们使用梯度下降法进行求解。

       梯度下降法的基本流程如下：

       （1）随机选择开一个初始点；

       （2）选择梯度下降的方向；

       （3）选择步长；

       （4）更新点；

       （5）重复（2）、（3）、（4）步知道满足终止条件。

       代码实现梯度下降法：

def LRGradientDescent(feature, label, maxIteration, alpha):
    '''
    使用梯度下降法训练逻辑回归模型
    :param feature: 特征
    :param label: 标签
    :param maxIteration: 最大迭代次数
    :param alpha: 学习率α
    :return: 返回权重矩阵
    '''
    n = np.shape(feature)[1]  # 特征的个数
    w = np.mat(np.ones((n, 1)))  # 初始化权重矩阵
    i = 0 # 定义指标， 用于与最大迭代次数进行比较
    while i <= maxIteration:  # 当指标小于最大迭代次数时
        i += 1
        sig = sigmoid(feature * w)  # 调用sigmoid函数计算sigmoid的值
        error = label - sig
        w = w + alpha * feature.T * error  # 权重修正
        if i % 100 == 0:
            print("迭代", str(i), "时的错误率为：", str(errorRate(sig, label)))
    return w

三、算法测试

1、数据集：分为训练集和测试集

（1）训练集

（2）测试集

2、加载数据集

       我们此处使用如下方法加载数据集，也可使用其他的方式进行加载，此处可以参考我的另外一篇文章《Python两种方式加载文件内容》。加载文件内容代码如下：

def loadData(fileName):
    '''
    加载测试数据
    :param fileName: 文件名
    :return: 返回特征和标签
    '''
    f = open(fileName)  # 打开训练数据集所在的文档
    feature = []  # 存放特征的列表
    label = []  # 存放标签的列表
    for row in f.readlines():
        f_tmp = []  # 存放特征的中间列表
        l_tmp = []  # 存放标签的中间列表
        number = row.strip().split("t")  # 得到每行特征和标签
        f_tmp.append(1)  # 设置偏置项
        for i in range(len(number) - 1):
            f_tmp.append(float(number[i]))
        l_tmp.append(float(number[-1]))
        feature.append(f_tmp)
        label.append(l_tmp)
    f.close()  # 关闭文件，这个操作很重要
    return np.mat(feature), np.mat(label)

3、保存权重值

       训练数据集，得到权重值，使用如下方法保存权重值：

def saveWeight(fileName, weight):
    '''
    保存权重矩阵
    :param fileName: 保存后的文件名
    :param weight: 权重矩阵
    :return:
    '''
    m = np.shape(weight)[0]
    f = open(fileName, "w")
    weight_list = []
    for i in range(m):
        weight_list.append(str(weight[i ,0]))
    f.write("t".join(weight_list))
    f.close()

4、使用训练得到的权重对测试集进行分类

'''
分类算法（线性二分类）：logistic Regression
'''

from LogisticRegression.LogisticRegression_train import sigmoid
import numpy as np

def loadFile(fileName, num):
    '''
    加载测试集
    :param fileName:
    :param num:
    :return: 返回特征
    '''
    f = open(fileName)
    feature = []
    for row in f.readlines():
        f_tmp = []
        number = row.strip().split("t")
        if len(number) != num - 1:  # 排除测试集中不符合要求的数据
            continue
        f_tmp.append(1)  # 设置偏置项
        for i in number:
            f_tmp.append(float(i))
        feature.append(f_tmp)
    f.close()
    return np.mat(feature)

def loadWeights(weights):
    '''
    加载权重值
    :param weights: 权重所在的文件位置
    :return: 权重矩阵
    '''
    f = open(weights)
    w = []
    for row in f.readlines():
        number = row.strip().split("t")
        w_tmp = []
        for i in number:
            w_tmp.append(float(i))
        w.append(w_tmp)
    f.close()
    return np.mat(w)

def predict(feature, w):
    '''
    对测试数据进行预测
    :param feature: 测试数据的特征
    :param w: 权重
    :return: 预测结果
    '''
    sig = sigmoid(feature * w.T)
    n = np.shape(sig)[0]
    for i in range(n):
        if sig[i, 0] < 0.5:
            sig[i, 0] = 0.0
        else:
            sig[i, 0] = 1.0
    return sig

def saveResult(fileName, result):
    '''
    保存预测结果
    :param file_name: 结果文件名
    :param result: 结果值
    :return:
    '''
    m = np.shape(result)[0]
    res = []
    for i in range(m):
        res.append(str(result[i, 0]))
    f = open(fileName, "w")
    f.write("t".join(res))
    f.close()

if __name__ == "__main__":
    path = "./data/"  # 数据集的存放路径
    w = loadWeights("weights")
    n = np.shape(w)[1]
    lr_test_data = loadFile(path + "test.txt", n)
    sig = predict(lr_test_data, w)
    saveResult("resultData", sig)

5、测试集分类如下图所示

        你们在此过程中遇到了什么问题，欢迎留言，让我看看你们都遇到了哪些问题。

最后

以上就是热心钻石为你收集整理的Python实现Logistic Regression（逻辑回归模型）算法的全部内容，希望文章能够帮你解决Python实现Logistic Regression（逻辑回归模型）算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。