推荐系统3：基于项目的协同过滤及矩阵分解

上文中我们说了基于用户的协同过滤的问题，但是与之俱来的是计算的数据量爆炸的问题，每个用户之间都要进行一次比较，假如有N个用户，那么总的比较次数就应该是N*(N-1)/2，随着用户数量的增加，比较的次数就会增大。

所以提出基于项目的协同过滤：

基于项目的协同过滤（IBCF）背后的思想是，如果两个项目从相同用户获得的评级相似，那么这两个项目是相似的。

这样，我们把计算不同用户之间的相似性的问题，转换到了计算不同客观事物，比如电影之间的相似性的问题。一般来说，用户的数量远远超过物品的数量的情形比较适合基于项目的协同过滤，如果用户数量比项目数量少，那么基于用户的协调过滤是可以考虑的。

基于项目的协同过滤基本上与基于用户的协同过滤方法一致，不过是在计算的时候，表格里的每一行是电影，或者项目，而不再是用户了。

矩阵分解

矩阵分解方法可以发掘用户与项目之间的潜在的特征。

假设在矩阵分解中，我们有U个用户，每个用户有K个特征描述。那么，我们将会得到一个U*K的用户信息矩阵。有D个项目，每个项目也有K个特征描述，那么我们会有一个D*K的项目信息矩阵。

用户矩阵与项目矩阵的转置的乘积将会得到一个U*D的矩阵。

U个用户对项目有了一些评分。我们可以根据用户对于项目的评分，来判断用户对某个项目的喜好程度。

下面以一个例子说明矩阵分解：

下表中描述的是编号为1,2,3,4,5的用户分别对编号1,2,3,4,的电影进行评分的表格。

我们的任务是，给Actual列的空值进行填充。这些空值代表用户尚未给予评分。

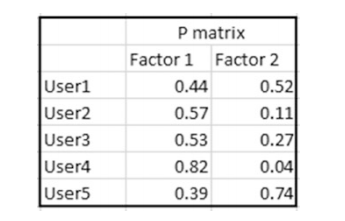
P矩阵指的是U*K的用户矩阵。Q矩阵指的是K*D的项目矩阵的转置矩阵。

本例假定K=2，也就是用户具有两个特征。本例中，一共有五个用户，U=5.一共有四部电影，D=4

1.随机初始化P矩阵的值。（一般介于0-1之间）

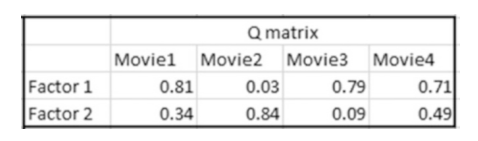
2.随机初始化项目矩阵的转置矩阵。（一般介于0-1之间）

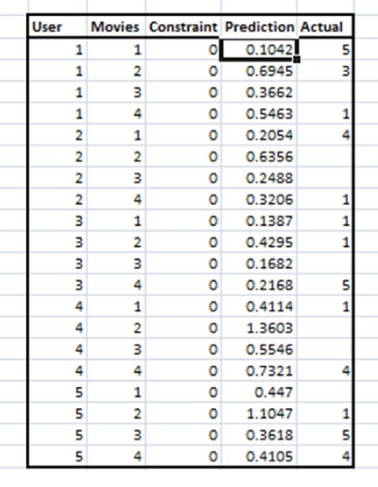
3.计算P*Q矩阵的值

4.随机初始化P和Q矩阵的值，分别计算均方误差，以达到最小误差为目的

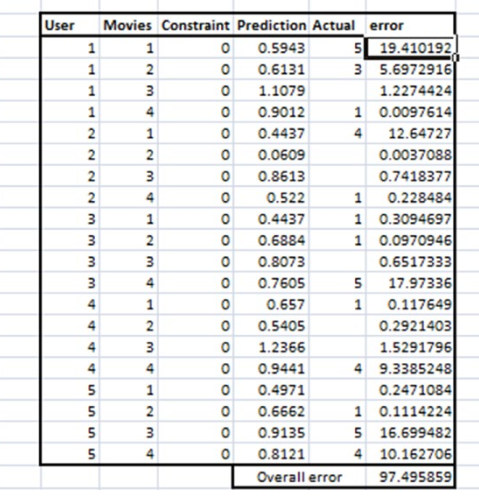
目标：随机初始化P和Q的值，使得综合误差最小。

约束条件：评分项不得高于5或者低于1（评分介于1-5之间）

5.得到最优的初始化P和Q矩阵的值

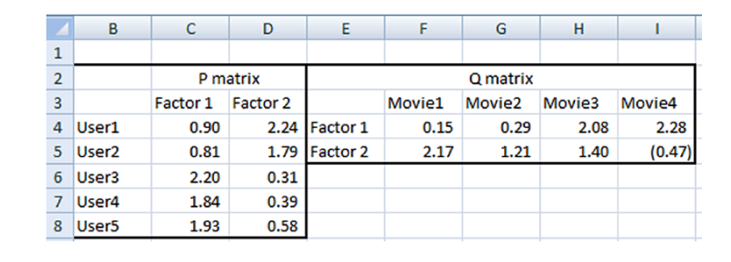
根据矩阵的值，计算用户对于未知项目的评分。

在具体实现过程中，使用Excel达到的效果实际上是用了梯度下降法。我们来看看python是怎么具体实现的：

1.导入包，读取数据

2. 用户去重

3. 电影去重

4.添加索引

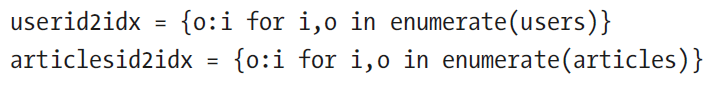
5.获取不重复的用户数量及电影数量

6. 定义误差计算公式RMSE

7. 导包

8. 优化

9. 获取用户矩阵

10. 获取电影矩阵

最后

以上就是甜甜鸡最近收集整理的关于推荐系统3：基于项目的协同过滤及矩阵分解的全部内容，更多相关推荐系统3：基于项目内容请搜索靠谱客的其他文章。