peak finder（找峰点）

1. 一维数组找峰点
2. 二维数组
3. 玩一下代码

1. 一维数组找峰点

FM(find middle,自己给算法起个名字，不知道中文叫啥)
第二个位置是一个峰点，当且仅当 b>a,b>c 。如果 i>h ,则第九个位置是峰点。

在大数据集上，试图找到一个峰点，返回他的索引，怎么找最好？

最直接的其实就是遍历一遍数组，比较之后找到一个最大的。但我们的要求是找到一个峰点，并没有要求一定是最高点。
问：这样的方法是最好的吗？

很明显不是最好的啦，还问。。。

很明显，从中间切一下，就省很多时间。
给定n 维数组A，算法如下：

1. 选中数组的中间元素 An2 ,并且对比他左右的元素
2. 如果他大于或等于他左右的元素，则这个点为峰点，返回 n2 ,
3. 如果右边的元素大于中间的元素，则下一次的算法用在右边的数组，且不包含中间元素
4. 如果左边的元素大于中间的元素，则下一次的算法用在左边的数组，且不包含中间元素

运行时间分析
我们把n维数组转换成 n2 ,复杂度分析如下：

2.二维数组

二维数组的峰点可以定义为：给定矩阵M，可以找到一点 M[i][j] ,使得该点大于等于它的邻居（ M[i+1][j],M[i−1][j],M[i][j−1],M[i][j+1] ）,如果它是边界点，则大于邻居点即峰点。

算法步骤：
给定nxm矩阵M,有:

1.在第 j=m2 列，作为一个一维数组，找这一列中的全局最大值
2. 选择在全局最大值的那一行i,如果 M[i−1][j]<M[i][j],且M[i][j]>M[i+1][j] ，则 M[i][j] 为我们找的峰点
3. 如果 M[i−1][j]>M[i][j] ,则将数组切分为两半，在左边的数据接着按照先前的做法寻找峰点。

算法原理如图所示：

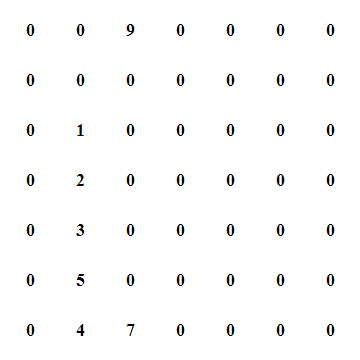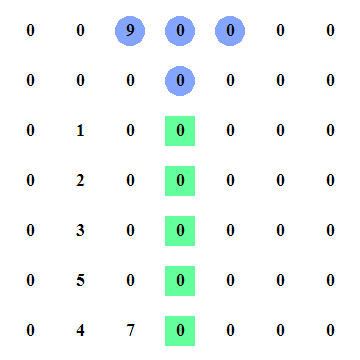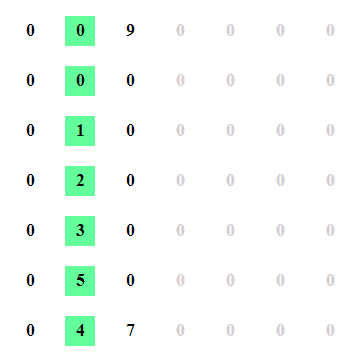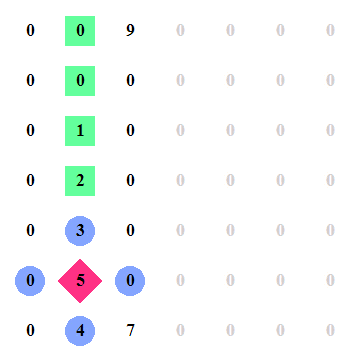
3.玩一下代码

class Solution(object):
def peakFind(self,nums):
return self.helpSearch(nums,0,len(nums)-1)
def helpSearch(self,nums,start,end):
if start == end :
return start
if end - start == 1:
return [end,start][nums[start] > nums[end]]
mid = int((start + end)/2)
if nums[mid] < nums[mid-1]:
return self.helpSearch(nums,start,mid-1)
if nums[mid] < nums[mid + 1]:
return self.helpSearch(nums , mid + 1,end)
return mid
if __name__=="__main__":
series = [0,0,0,2,0,0,0,-2,0,0,0,2,0,0,0,-2,0,0,0,76,-9,-444]
solution = Solution()
mid = solution.peakFind(series)
print(mid)

最后

以上就是迷你凉面最近收集整理的关于peak finder（找峰点）的全部内容，更多相关peak内容请搜索靠谱客的其他文章。