深度学习——循环神经网络/递归神经网络（RNN）及其改进的长短时记忆网络（LSTM）

一、循环神经网络简介

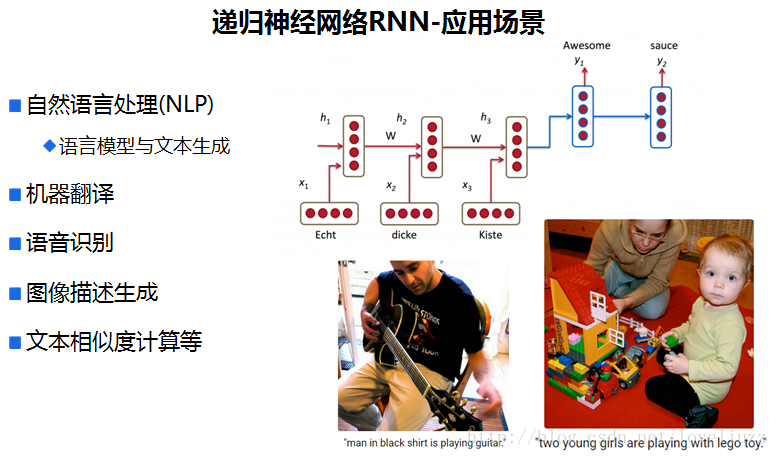
二、循环神经网络的结构

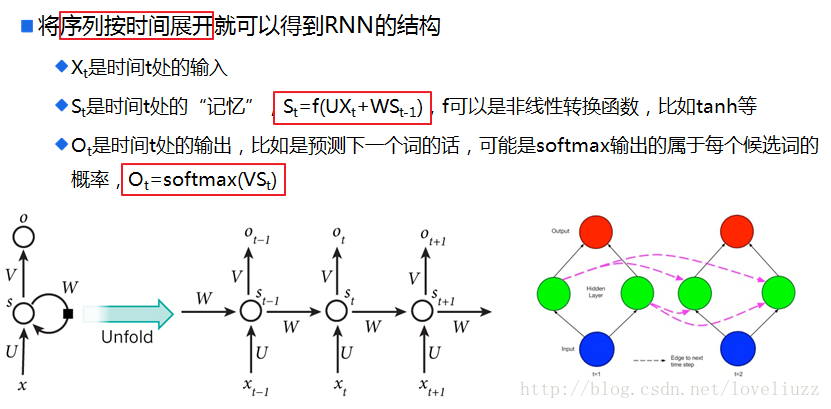
三、循环神经网络的前向传播与反向传播

（一）RNN前向传播

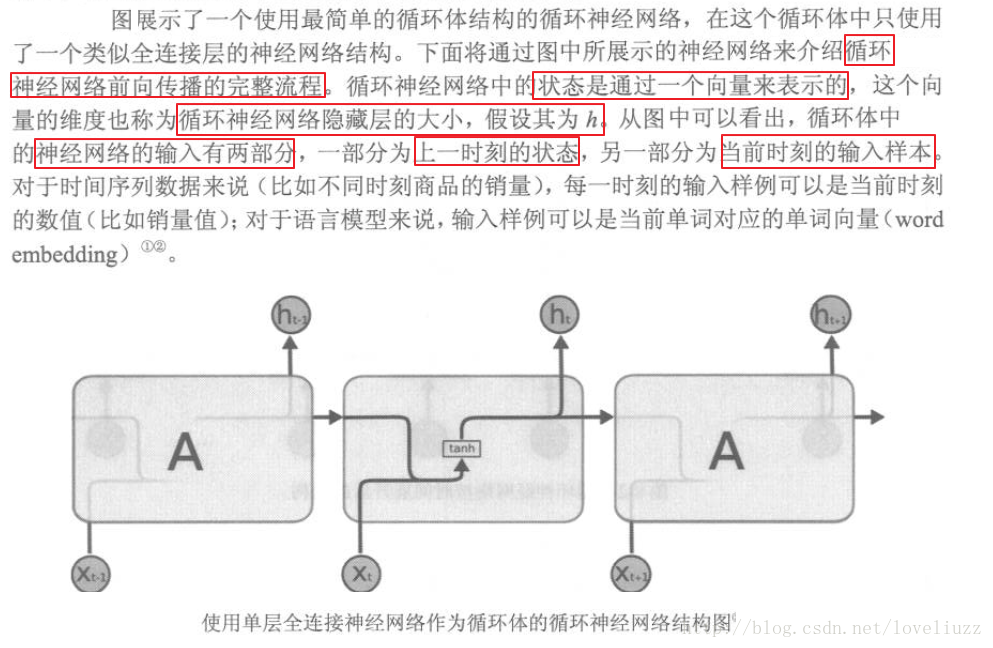
前向传播总结：

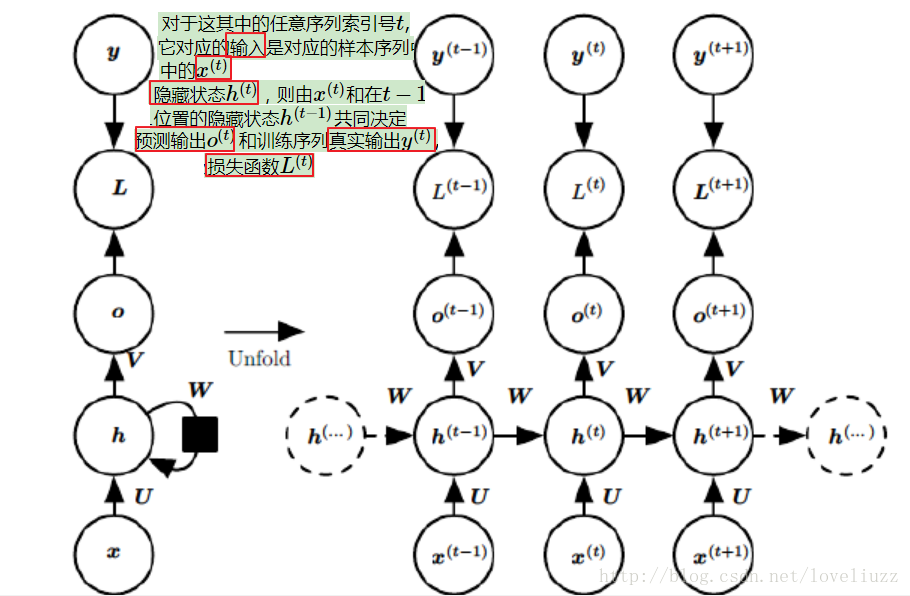
（二）RNN反向传播

（三）RNN网络的缺点

四、长短时记忆——LSTM结构

（一）LSTM结构的引入

在RNN模型里，每个序列索引位置t都有一个隐藏状态h(t)。如果我们略去每层都有的

o(t)、L(t)、y(t)，则RNN的模型图一可以简化成如下图二的形式：在隐藏状态h(t)由x(t)和h(t−1)得到。

得到的h(t)一方面用于当前层的模型损失计算，另一方面用于计算下一层的h(t+1)。

由于RNN梯度消失的问题，大牛们对于序列索引位置t的隐藏结构做了改进，可以说通过一些技巧让隐藏结构复杂来

避免梯度消失的问题，这样的特殊RNN就是我们的LSTM。下面介绍最常见的LSTM，其结构图结构如下：

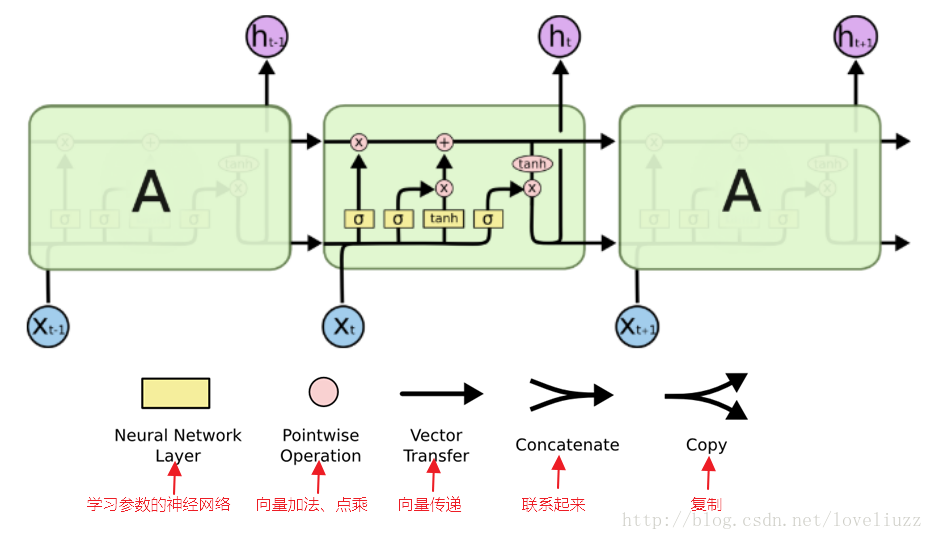
（二）LSTM内部结构解析

 下面一步步对LSTM模型在每个序列索引位置t时刻的内部结构进行解析。

1、LSTM模型的关键——细胞状态(Cell State)

在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态h(t)，还多了另一个隐藏状态，如图中上面的长横线。

这个隐藏状态我们一般称为细胞状态(Cell State)，记为C(t)。LSTM单元上面的这条直线代表了LSTM的状态（state)，

它会贯穿所有串联在一起的LSTM单元，从第一个LSTM单元一直流向最后一个LSTM单元，其中只有少量的线性干预与改变。

细胞状态(Cell State)类似于传送带，直接在整个链上运行，只有一些少量的线性交互，信息在上面流传保持不变很容易。

2、LSTM模型——门控结构（Gates）

 细胞状态（cell state）在这条隧道中传递时，LSTM单元可以对状态（state）添加或删除信息，

这些对信息流的修改操作由LSTM中的门控结构Gates控制。

这些门控结构Gates中包含了一个sigmoid层和一个按位做乘法的操作，这个sigmoid层的输出是0到1之间的值，

它控制了信息传递的比例。如果为0代表：不允许信息传递；如果为1代表：让信息全部通过。

每个LSTM单元包含了3个这样的（包含了一个sigmoid层和一个按位做乘法的操作）门控结构Gates，

即：LSTM在在每个序列索引位置t的门一般包括三种，分别为：遗忘门，输入门和输出门，用来维护和控制单元的状态信息。

凭借着对状态信息的储存和修改，LSTM单元就可以实现长程记忆。

（1）遗忘门（forget gate）

顾名思义，在LSTM中遗忘门是控制是否遗忘的，即以一定的概率控制是否遗忘上一层的隐藏细胞状态。

如语言模型中，细胞状态可能包含性别信息(“他”或者“她”)，当我们看到新的代名词的时候，可以考虑忘记旧的数据。

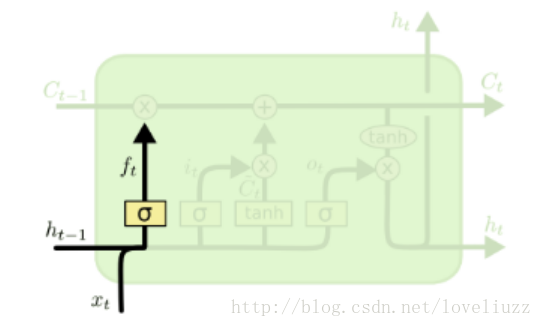
 图中输入的有上一序列的隐藏状态h(t−1)和本序列数据x(t)，通过一个激活函数，一般是sigmoid，

得到遗忘门的输出f(t)。由于sigmoid的输出f(t)在[0,1]之间，因此输出f(t)代表了遗忘上一层隐藏细胞状态的概率。

用数学表达式即为：
    

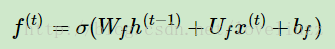
其中Wf,Uf,bf为线性关系的系数和偏倚，和RNN中的类似，σ为sigmoid激活函数。

（2）输入门（input gate）

在循环神经网络”遗忘“了部分之前的状态后，还需要从当前的输入补充最新记忆。

输入门（input gate）负责处理当前序列位置的输入，它的子结构如下图：

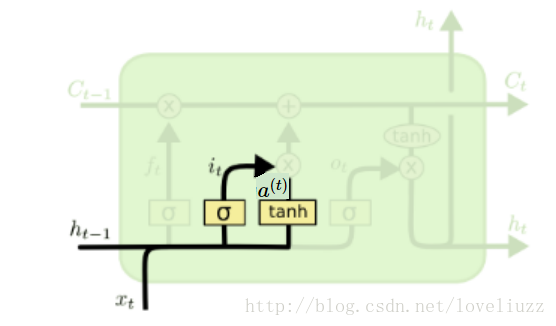
从图中可以看到输入门由两部分组成，第一部分使用了sigmoid激活函数，输出为i(t),

第二部分使用了tanh激活函数，输出为a(t), 两者的结果后面会相乘再去更新细胞状态。

用数学表达式即为：

（3）细胞状态（ceil state）更新

前面的遗忘门和输入门的结果都会作用于细胞状态C(t)。来看从细胞状态C(t−1)如何得到C(t)。如下图所示：

（4）输出门

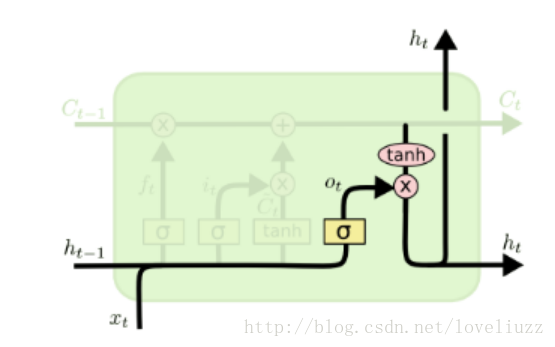
(三)对于LSTM结构的另一种理解

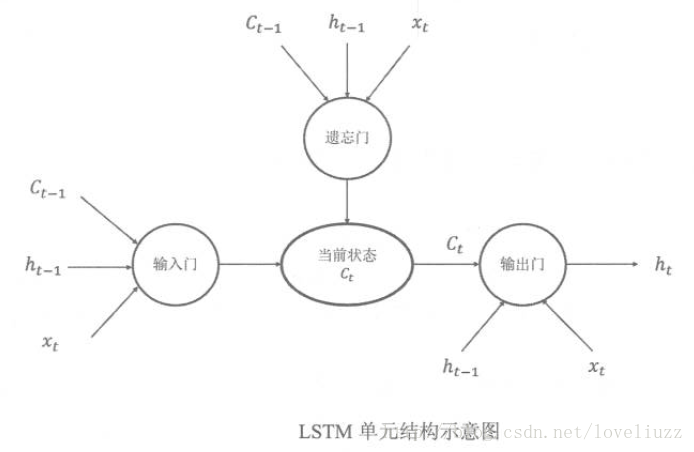
（四)LSTM结构的前向传播与反向传播

1、LSTM前向传播

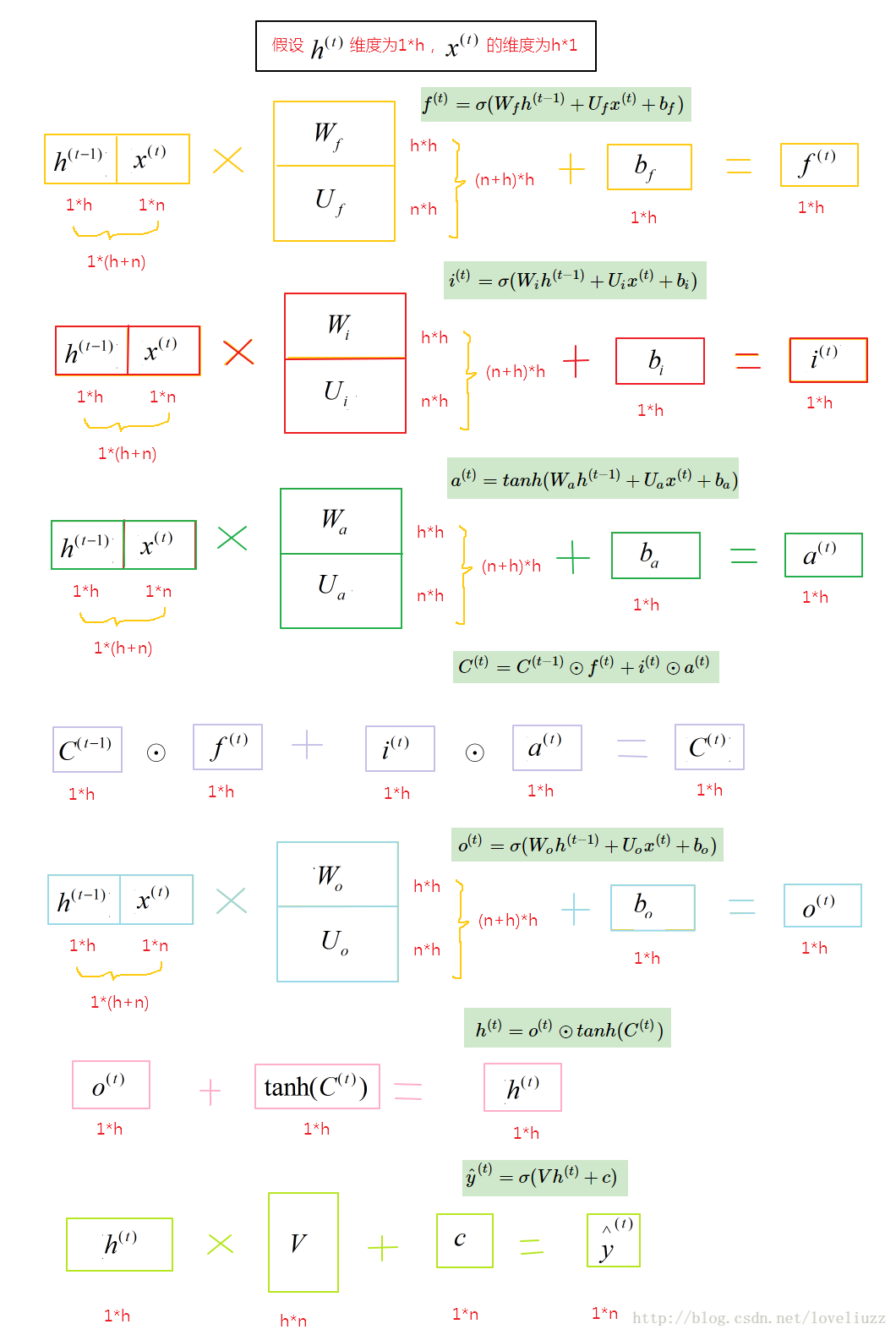
2、LSTM反向传播

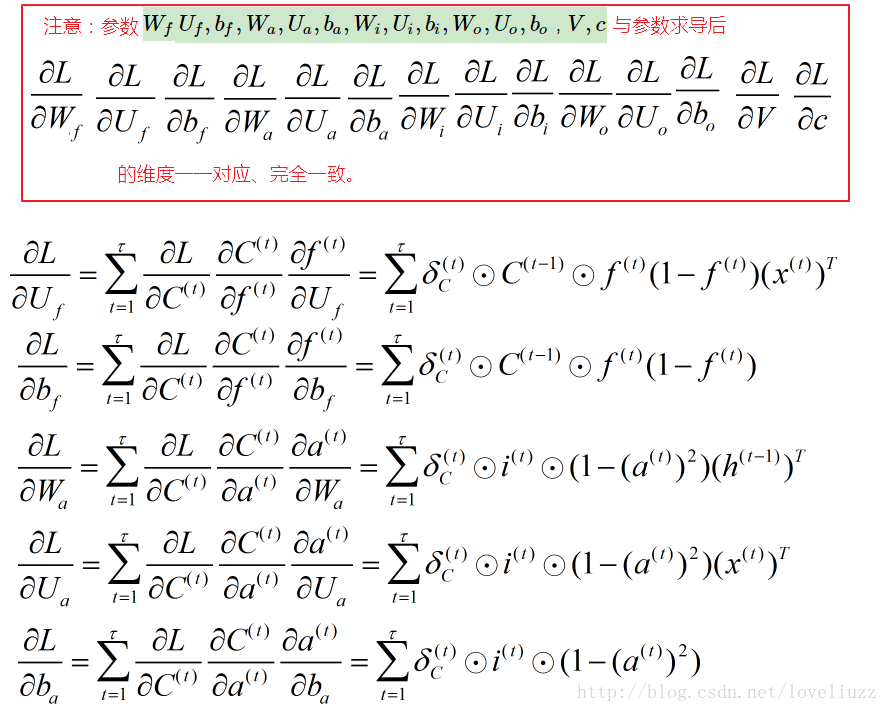
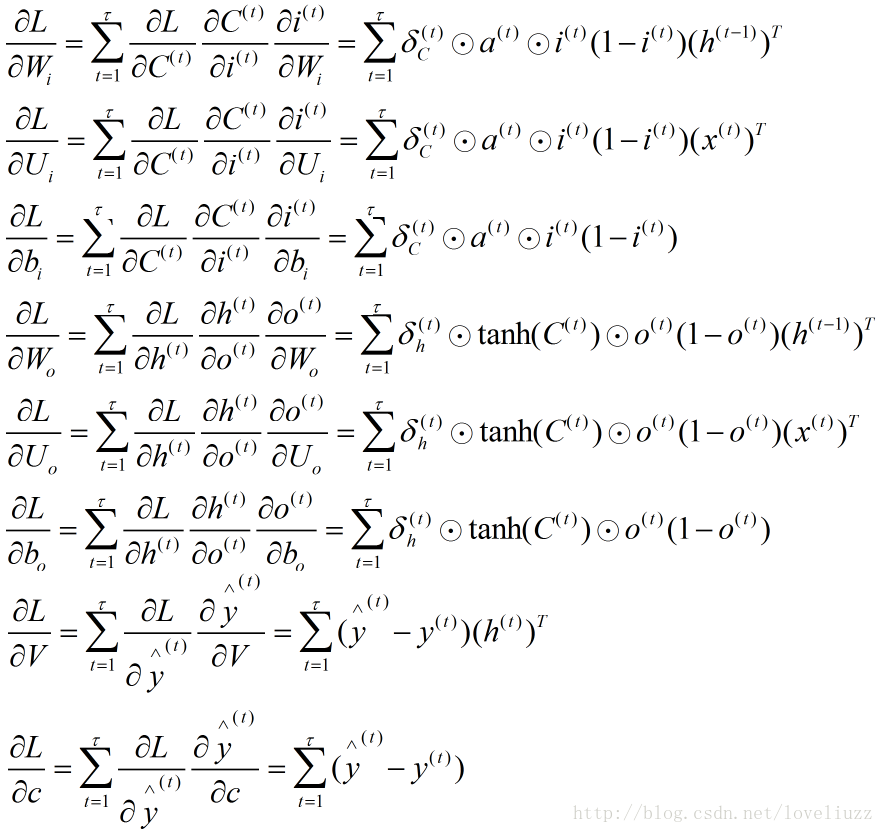
五、循环神经网络的变形

六、双向循环神经网络（Bi-RNN）

    Bi-RNN又叫双向RNN，采用了两个方向的RNN网络，RNN网络擅长的是对于连续数据的处理，不仅可以学习它的正向规律，还可以学习它的反向规律。这样将正向和反向结合的网络会比单向的循环神经网络有更高的拟合度，如：预测一个语句中缺失的词语，则需要根据上下文来进行预测。双向RNN处理过程就是在正向传播的基础上再进行一次反向传播，而且这两个都连接着一个输出层。这个结构提供给输出层输入序列中，每一个点完整的过去和未来的上下文信息。

     在按照时间正向运算完之后，网络又从时间的最后一项反向地运算一遍，即：把t3时刻的输入与默认值0一起生成反向的out3，再把反向out3当成t2时刻的输入与原来t2时刻输入一起生成反向地out2，以此类推，直到第一个时序数据。在大多数应用里面，基于时间序列与上下文有关的、类似NLP中自动回答类的问题，一般都是使用双向LSTM+LSTM/RNN横向扩展来实现的，效果非常好。

    注意：双向循环神经网络商务输出是2个，正向一个，反向一个，最终会把输出结果concat并联在一起，然后交给后边的层来处理，例如：数据输入[batch,nhidden]，输出就会变成[batch,nhidden*2]。

七、循环神经网络的dropout

八、python实现LSTM代码

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu

import numpy as np

#输出单元激活函数
def softmax(x):
    x = np.array(x)
    max_x = np.max(x)
    return np.exp(x-max_x)/np.sum(np.exp(x-max_x))

#定义sigmoid函数
def sigmoid(x):
    return 1./(1 + np.exp(-x))

#定义sigmoid函数的导数
def sigmoid_derivative(values):
    return values(1-values)

#定义tanh函数的导数
def tanh_derivative(values):
    return 1.- values**2

class MyLSTM():
    def __init__(self,n,h):
        self.n = n  #n:输入样本特征维度数量(如：词向量维度n*1)
        self.h = h  #h：隐藏状态/隐藏层的神经元的维度(h*1)

        #初始化权重向量
        self.whf,self.wxf,self.bf = self.init_wh_wx_b()
        self.whi,self.wxi,self.bi = self.init_wh_wx_b()
        self.wha,self.wxa,self.ba = self.init_wh_wx_b()
        self.who,self.wxo,self.bo = self.init_wh_wx_b()
        self.wy,self.by = np.random.uniform(-np.sqrt(1.0/self.h),np.sqrt(1.0/self.h),
                                            (self.n,self.h)),
                          np.random.uniform(-np.sqrt(1.0/self.h),np.sqrt(1.0/self.h),
                                            (self.n,1))

    #初始化wh,wx,b
    def init_wh_wx_b(self):
        wh = np.random.uniform(-np.sqrt(1.0/self.h),np.sqrt(1.0/self.h),
                               (self.h,self.h))
        wx = np.random.uniform(-np.sqrt(1.0/self.n),np.sqrt(1.0/self.n),
                               (self.h,self.n))
        b = np.random.uniform(-np.sqrt(1.0/self.n),np.sqrt(1.0/self.n),
                              (self.h,1))
        return wh,wx,b

    # LSTM门控结构的状态初始化
    def init_state(self,T):
        #遗忘门
        ft = np.array([np.zeros((self.h, 1))] * (T + 1))
        #输入门
        it = np.array([np.zeros((self.h, 1))] * (T + 1))
        at = np.array([np.zeros((self.h, 1))] * (T + 1))
        #细胞状态
        ct = np.array([np.zeros((self.h, 1))] * (T + 1))
        #输出门
        ot = np.array([np.zeros((self.h, 1))] * (T + 1))
        ht = np.array([np.zeros((self.h, 1))] * (T + 1))
        #预测输出
        yt = np.array([np.zeros((self.n, 1))] * T)

        return {
            "ft":ft,"it":it,"at":at,"ct":ct,"ot":ot,"ht":ht,"yt":yt
        }
    #前向传播，单个x
    def forward_prop(self,x):
        #向量时间长度
        T = len(x)
        #初始化LSTM门控结构各个状态向量
        states = self.init_state(T)

        for t in range(T):
            #前一时刻的隐藏层状态
            ht_pre = np.array(states["ht"][t-1]).reshape(-1,1)
            #遗忘门
            states["ft"][t] = self.calcu_gate(self.whf,self.wxf,self.bf,ht_pre,x[t],sigmoid)
            #输入门
            states["it"][t] = self.calcu_gate(self.whi,self.wxi,self.bi,ht_pre,x[t],sigmoid)
            states["at"][t] = self.calcu_gate(self.wha,self.wxa,self.ba,ht_pre,x[t],np.tanh)
            #更新细胞状态,ct = ft * ct_pre + it * at
            states["ct"][t] = states["ft"][t] * states["ct"][t-1] + states["it"][t] * states["at"][t]
            #输出门
            states["ot"][t] = self.calcu_gate(self.who,self.wxo,self.bo,ht_pre,x[t],sigmoid)
            states["ht"][t] = states["ot"][t] * np.tanh(states["ct"][t])
            #预测输出
            states["yt"][t] = softmax(np.dot(self.wy,states["ht"][t])+self.by)

            return states

    #计算各个门的输出
    def calcu_gate(self,wh,wx,b,ht_pre,x,activation):
        return activation(np.dot(wh,ht_pre)+np.dot(wx,x)+b)

    #预测输出,单个x
    def predict(self,x):
        states = self.forward_prop(x)
        pre_y = np.argmax(states["yt"].reshape(len(x),-1),axis=1)
        return pre_y

    #计算损失,softmax交叉熵损失函数，(x,y)为多个样本
    def loss(self,x,y):
        cost = 0
        for i in range(len(y)):
            states = self.forward_prop(x[i])
            #取出y[i]中每一时刻对应的预测值
            pre_yi = states["yt"][range(len(y[i])),y[i]]
            cost -= np.sum(np.log(pre_yi))

        #统计所有y中的词的个数，计算平均损失
        N = np.sum([len(yi) for yi in y])
        avg_cost = cost/N

        return avg_cost

    #初始化偏导数dwh,dwx,db
    def init_wh_wx_b_grad(self):
        dwh = np.zeros(self.whi.shape)
        dwx = np.zeros(self.wxi.shape)
        db = np.zeros(self.bi.shape)

        return dwh,dwx,db
    #求梯度,(x,y)为一个样本
    def bptt(self,x,y):
        dwhf,dwxf,dbf = self.init_wh_wx_b_grad()
        dwhi,dwxi,dbi = self.init_wh_wx_b_grad()
        dwha,dwxa,dba = self.init_wh_wx_b_grad()
        dwho,dwxo,dbo = self.init_wh_wx_b_grad()
        dwy,dby = np.zeros(self.wy.shape),np.zeros(self.by.shape)
        # 初始化 delta_ct，因为后向传播过程中，此值需要累加
        delta_ct = np.zeros((self.h,1))

        #前向计算
        states = self.forward_prop(x)
        #目标函数对输出y的偏导数,y_hat - 1
        delta_z = states["yt"]
        delta_z[range(len(y)),y] -= 1

        for t in np.arange(len(y))[::-1]:
            # 输出层wy, by的偏导数，由于所有时刻的输出共享输出权值矩阵，故所有时刻累加
            dwy += np.dot(delta_z[t],states["ht"][t].reshape(1,-1))
            dby += delta_z[t]
            #目标函数对隐藏状态ht的偏导数
            delta_ht = np.dot(self.wy.T,delta_z[t])
            #目标函数对各个门及状态单元的偏导数
            delta_ct += delta_ht * states["ot"][t] *(1-np.tanh(states["ct"][t])**2)
            delta_ft = delta_ct * states["ct"][t-1]
            delta_it = delta_ct * states["at"][t]
            delta_at = delta_ct * states["it"][t]
            delta_ot = delta_ht * np.tanh(states["ct"][t])

            delta_ft_net = delta_ft * states["ft"][t] *(1-states["ft"][t])
            delta_it_net = delta_it * states["it"][t] *(1-states["it"][t])
            delta_at_net = delta_at * (1-states["at"][t] ** 2)
            delta_ot_net = delta_ot * states["ot"][t] *(1-states["ot"][t])

            # 更新各权重矩阵的偏导数，由于所有时刻共享权值，故所有时刻累加
            dwhf,dwxf,dbf = self.calcu_grad_delta(dwhf,dwxf,dbf,delta_ft_net,states["ht"][t-1],x[t])
            dwhi,dwxi,dbi = self.calcu_grad_delta(dwhi,dwxi,dbi,delta_it_net,states["ht"][t-1],x[t])
            dwha,dwxa,dba = self.calcu_grad_delta(dwha,dwxa,dba,delta_at_net,states["ht"][t-1],x[t])
            dwho,dwxo,dbo = self.calcu_grad_delta(dwho,dwxo,dbo,delta_ot_net,states["ht"][t-1],x[t])

            return [dwhf,dwxf,dbf,
                    dwhi,dwxi,dbi,
                    dwha,dwxa,dba,
                    dwho,dwxo,dbo,
                    dwy,dby]

    #更新各权重矩阵的偏导数
    def calcu_grad_delta(self,dwh,dwx,db,delta_net,ht_prev,x):
        dwh += delta_net * ht_prev
        dwx += delta_net * x
        db += delta_net

        return dwh,dwx,db

    #计算梯度，（x,y）为一个样本
    def sgd_step(self,x,y,learning_rate):
        dwhf, dwxf, dbf,
        dwhi, dwxi, dbi,
        dwha, dwxa, dba,
        dwho, dwxo, dbo,
        dwy, dby = self.bptt(x,y)

        #更新权重矩阵
        self.whf,self.wxf,self.bf = self.update_wh_wx_b(learning_rate,self.whf,self.wxf,self.bf,dwhf,dwxf,dbf)
        self.whi,self.wxi,self.bi = self.update_wh_wx_b(learning_rate,self.whi,self.wxi,self.bi,dwhi,dwxi,dbi)
        self.wha,self.wxa,self.ba = self.update_wh_wx_b(learning_rate,self.wha,self.wxa,self.ba,dwha,dwxa,dba)
        self.who,self.wxo,self.bo = self.update_wh_wx_b(learning_rate,self.who,self.wxo,self.bo,dwho,dwxo,dbo)

        self.wy,self.by = self.wy - learning_rate * dwy,self.by - learning_rate * dby

    # 更新权重矩阵函数
    def update_wh_wx_b(self,learning_rate,wh,wx,b,dwh,dwx,db):
        wh -= learning_rate * dwh
        wx -= learning_rate * dwx
        b -= learning_rate * db

        return wh,wx,b

    #训练LSTM
    def train(self,x_train,y_train,learning_rate=0.005,n_epoch=5):
        losses = []
        num_examples = 0

        for epoch in range(n_epoch):
            for i in range(len(y_train)):
                #计算梯度
                self.sgd_step(x_train,y_train,learning_rate)
                num_examples += 1

            # 计算损失函数
            loss = self.loss(x_train,y_train)
            losses.append(loss)
            print("epoch {0}:loss {1}".format(epoch+1,loss))
            if len(losses) > 1 and losses[-1] > losses[-2]:
                learning_rate *= 0.5    #当损失值开始升高时，降低学习率
                print("decrease learning rate to:",learning_rate)

最后

以上就是神勇蜗牛为你收集整理的深度学习——循环神经网络/递归神经网络（RNN）及其改进的长短时记忆网络（LSTM）的全部内容，希望文章能够帮你解决深度学习——循环神经网络/递归神经网络（RNN）及其改进的长短时记忆网络（LSTM）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。