疏系数模型的R实现

疏系数模型是ARIMA模型的一种特殊情况，原来ARIMA模型中有一部分系数缺失了，那么这个模型就是疏系数模型。
1.模型简介
如果是自回归部分有缺失的系数，那么该疏系数模型就可以记为：
ARIMA((p1,…pm),d,q)
如果只是是移动平均部分有缺失的系数，那么该疏系数模型就可以简记为：
ARIMA（p,d,(q1,…1n))
如果自回归和移动平均部分都有系数缺失的话，该模型就可以简记为：
ARIMA((p1,…,pm),d,(q1,…,qn))
2.建模过程
（1）画出时序图，偏自相关图，自相关图（或者根据单位根检验）来判别时间序列的平稳性
（2）对非平稳时间序列进行差分处理，使其平稳化
（3）对差分处理之后的序列进行白噪声检验，若是白噪声序列就停止建模，若是非白噪声序列就对该序列进行建模
（4）疏系数模型和ARIMA模型有点不同的地方就在于，疏系数模型在定阶的过程中，不能让系统根据模型的最高阶数自动完成所有的参数估计，需要指定疏系数的位置（计算各参数值）
（5)对模型进行参数的显著性检验和残差的白噪声检验
3.建立模型
数据采用美国1917年到1975年妇女人均生育率序列建模
（1）画出其时序图，和利用单位根检验来判断其平稳性。

library(tseries)
library(forecast)
library(zoo)
a=read.table("C:/Users/MrDavid/data_TS/A1.18.csv",sep=",",header=T)
x=ts(a$fertility,start=1917)
plot(x,col=4,lwd=2,type="o",pch=8)
adf.test(x)

单位根检验如下：

从上述结果看，p=0.9628，远大于0.05，所以该序列非平稳。
（2)对其序列进行差分处理，然后对其差分序列进行平稳性检验。发现其一阶差分依旧非平稳，接着进行二阶差分，画出其时序图和进行平稳性检验

x.dif=diff(x,difference=2)
plot(x.dif,type="o",lwd=2,pch=8,col=4)
adf.test(x.dif)

二阶差分是个平稳序列
对其二阶差分序列进行白噪声检验

for (i in 1:3) print(Box.test(x.dif,lag=6*i))

非白噪声序列，可以进行建模
（3）画出其自相关图，偏自相关图

acf(x.dif,col=4,lwd=2)
pacf(x.dif,col=4,lwd=2)

（4)模型的定阶
自相关系数在1，4，5超出两倍标准差，偏自相关系数在1，4超出两倍标准差，所以拟合的模型为：
ARIMA((1,4),2,(1,4,5)).但是由于第一个参数不显著，我们将第一个参数也指定为0

x.fit=arima(x,order=c(4,2,5),transform.pars=F,fixed=c(0,0,0,NA,NA,0,0,NA,NA))
x.fit

（5)对模型进行显著性检验
对该模型残差进行白噪声检验：

for (i in 1:3) print(Box.test(x.fit$residual,lag=6*i))

残差序列为白噪声序列。
对参数进行显著性检验：

t2=-0.4931/0.1365
pt(t2,df=53,lower.tail=T)
t3=-0.9074/0.0803
pt(t3,df=53,lower.tail=T)
t4=1.0605/0.1595
pt(t4,df=53,lower.tail=F)
t5=-0.7986/0.1428
pt(t5,df=53,lower.tail=T)

现在所有参数都显著有效，所以模型拟合成功。
该模型为：

4.用模型来预测
预测未来5年的值

x.fore=forecast(x.fit,h=5)
x.fore

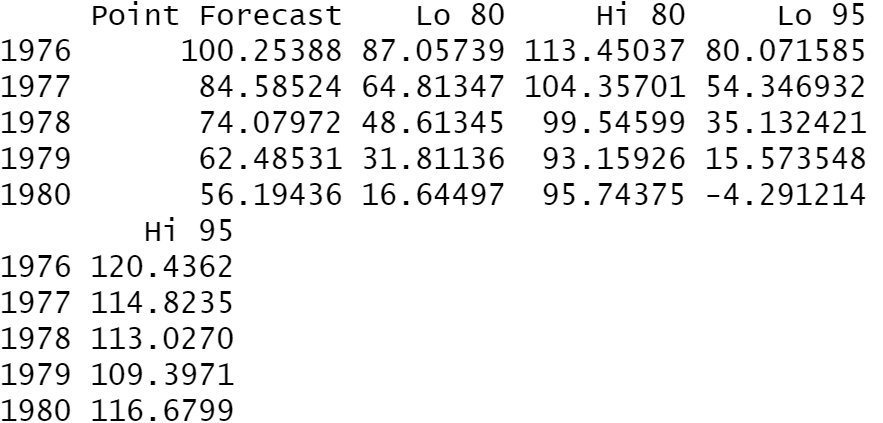
画出预测图：

L1=x.fore$fitted-1.96*sqrt(x.fit$sigma2)
U1=x.fore$fitted+1.96*sqrt(x.fit$sigma2)
L2=ts(x.fore$lower[,2],start=1917)
U2=ts(x.fore$upper[,2],start=1917)
c1=min(x,L1,L2)
c2=max(x,L1,L2)
plot(x,type="p",pch=8,xlim=c(1917,1975),ylim=c(c1,c2))
lines(x.fore$fitted,col=2,lwd=2)
lines(x.fore$mean,col=2,lwd=2)
lines(L1,col=4,lty=2)
lines(U1,col=4,lty=2)
lines(L2,col=4,lty=2)
lines(U2,col=4,lty=2)

最后

以上就是动听过客为你收集整理的疏系数模型的R实现的全部内容，希望文章能够帮你解决疏系数模型的R实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。