cv2.approxPolyDP函数实现轮廓线的多边形逼近

        实际项目需要拟合轮廓线，提取更贴合目标的四个点，于是找到了cv2.approxPolyDP函数。cv2.approxPolyDP() 使用了Douglas-Peucker算法，算法原理如下：

输入一组曲线点集合S，输出折线点集合T流程：

        step1、设阈值thresh，取A的起点A和终点B加入T；

        step2、取S中的一点C，使之距离A和B连成的直线最远；

        step3、如果距离大于阈值，则将C加入T；

        step4、分别递归AC与CB；

        step5、输出结果集T。

测试代码：

import cv2

mask = cv2.imread(r'C:UsersAdministratorDesktopaa.bmp', 0)  # read picture
mask[mask > 100] = 255
mask[mask != 255] = 0

im_show = cv2.cvtColor(mask, cv2.COLOR_GRAY2BGR)
countours, hierarchy = cv2.findContours(mask, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
for idx, cnt in enumerate(countours):
    print("cnt shape:", cnt.shape) #　(N, 1, 2)
    rect = cv2.minAreaRect(cnt)  # (cx, cy), (bw, bh), theta
    # epsilon = max(min(bw, bh) * 0.1, 5)
    print("rect:", rect)
    epsilon = 0.1 * cv2.arcLength(cnt, True)  # 计算轮廓线长度
    print("epsilon:", epsilon)
    approx = cv2.approxPolyDP(cnt, epsilon, True)
    print("approx:", approx.shape)
    cv2.drawContours(im_show, approx, -1, (0, 0, 255), 5) # dtype=np.int32

    points = approx.reshape((-1, 2))
    if points.shape[0] < 4:
        continue
    print("points shape:", points.shape)
cv2.imwrite(r'C:UsersAdministratorDesktopim_show.jpg', im_show)

结果：

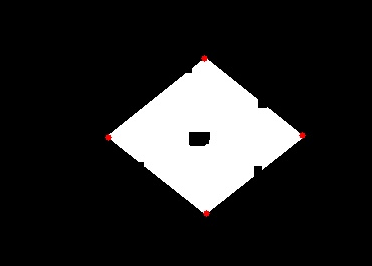
函数意义：

1、approxCourve= cv2.approxPolyDP(curve,epsilon,closed)

轮廓线多边形逼近。

参数解析：

        curve：轮廓点的集合。

        epsilon：指定近似精度的参数， 这是原始曲线和它的近似之间最大距离。

        closed：如果为true，则闭合近似曲线（其第一个和最后一个顶点为连接的）；否则，不闭合。

2、double arcLength(InputArray curve, bool closed)

函数用于计算封闭轮廓的周长或曲线的长度。

参数解析：

        curve：输入的二维点集（轮廓顶点），可以是 vector 或 Mat 类型。

        closed：用于指示曲线是否封闭。

3、double contourArea(InputArray contour, bool oriented = false)

计算轮廓面积。

参数解析：

        contour：输入的二维点集（轮廓顶点），可以是 vector 或 Mat 类型。

        oriented：面向区域标识符。有默认值 false。若为 true，该函数返回一个带符号的面积值，正负取决于轮廓的方向（顺时针还是逆时针）。若为 false，表示以绝对值返回。

最后

以上就是紧张煎蛋为你收集整理的cv2.approxPolyDP函数实现轮廓线的多边形逼近的全部内容，希望文章能够帮你解决cv2.approxPolyDP函数实现轮廓线的多边形逼近所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。