f(cos(x))=cos(n∗x) holds for all x.
Given two integers n and m, you need to calculate the coefficient of xm in f(x), modulo 998244353.
Input Format
Multiple test cases (no more than 100).
Each test case contains one line consisting of two integers n and m.
1≤n≤109,0≤m≤104.
Output Format
Output the answer in a single line for each test case.
样例输入
2 0 2 1 2 2
样例输出
998244352 0 2
题目来源
2017 ACM-ICPC 亚洲区(西安赛区)网络赛
题意: 把 f(x) 展开成多项式, 为 x^m 的 前面的系数是多少?
这个题: 推了半天- -- 规律找了半天; 然后 就差最后一个 公式 有n和m求 这个数
这个公式 就是 切比雪夫多项式
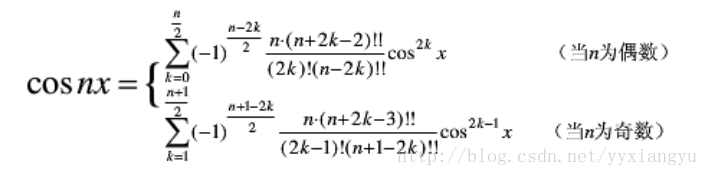
利用cox x 多项式 来解决 这样就可以 同奇同偶考虑

对于 每一项 我们可以 发现这样的规律 :

当 n,m 一奇一偶时, 结果为0
当 n为奇数时, m有第一项 没有 第0 项 第0项为0 第一项绝对值为n 判断正负 由 (n/2 )%2 来判断
当 n 为偶数时, m 有第0 项 没有第一项, 第0 项绝对值 为 1 正负由 (n/2)%2 来判断
当n,m同奇同偶时, 利用公式
AC 代码:
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cmath>
#include <math.h>
#include <cstring>
#include <string>
#include <queue>
#include <stack>
#include <stdlib.h>
#include <list>
#include <map>
#include <set>
#include <bitset>
#include <vector>
#define mem(a,b) memset(a,b,sizeof(a))
#define findx(x) lower_bound(b+1,b+1+bn,x)-b
#define FIN freopen("input.txt","r",stdin)
#define FOUT freopen("output.txt","w",stdout)
#define S1(n) scanf("%d",&n)
#define SL1(n) scanf("%I64d",&n)
#define S2(n,m) scanf("%d%d",&n,&m)
#define SL2(n,m) scanf("%I64d%I64d",&n,&m)
#define Pr(n) printf("%dn",n)
using namespace std;
typedef long long ll;
const double PI=acos(-1);
const int INF=0x3f3f3f3f;
const double esp=1e-6;
const int maxn=1e6+5;
const int MOD=998244353;
const int mod=998244353;
int dir[5][2]={0,1,0,-1,1,0,-1,0};
ll inv[maxn*2],fac[maxn];
ll gcd(ll a,ll b){ return b?gcd(b,a%b):a;}
ll exgcd(ll a,ll b,ll &x,ll &y){if(!b){x=1;y=0;return a;}ll ans=exgcd(b,a%b,x,y);ll temp=x;x=y;y=temp-a/b*y;return ans;}
ll lcm(ll a,ll b){ return b/gcd(a,b)*a;}
ll qpow(ll x,ll n){ll res=1;for(;n;n>>=1){if(n&1)res=(res*x)%MOD;x=(x*x)%MOD;}return res;}
ll inv1(ll b){return b==1?1:(MOD-MOD/b)*inv1(MOD%b)%MOD;}
ll inv2(ll b){return qpow(b,MOD-2);}
int n,m;
ll solve()
{
if(m>n)
{
return 0;
}
if(n&1)//
{
if(m%2==0){
return 0;
}
if(m==1)
{
if((n/2)%2==0)
return n;
else
return -n;
}
}
else
{
if(m&1){
return 0;
}
if(m==0)
{
if((n/2)%2==0)
return 1;
else
return -1;
}
}
ll ans=1;
for(int i=n-m+2;i<=n+m-2;i+=2)
{
ans= (ans*i)%MOD;
}
ans=(ans*n)%mod;
ll temp=1;
for(int i=1;i<=m;i++)
temp= (i*temp)%MOD;
ans= ans* inv2(temp)%MOD;
ans = ((n-m)/2)%2 == 0 ? ans:-ans;
return ans;
}
int main()
{
while(~scanf("%d %d",&n,&m))
{
ll ans=solve();
ans =(ans+MOD)%MOD;
printf("%lldn",ans%MOD);
}
return 0;
}
123
最后
以上就是帅气魔镜最近收集整理的关于2017 ACM-ICPC 亚洲区(西安赛区)网络赛 F. Trig Function(切比雪夫多项式)的全部内容,更多相关2017内容请搜索靠谱客的其他文章。

![[vijos P1518] [tyvj P1506] 河流](https://file2.kaopuke.com:8081/files_image/reation/bcimg2.png)






发表评论 取消回复