数据结构中涉及的排序算法

71 阅读 0 评论 47 点赞

我是靠谱客的博主可爱寒风，最近开发中收集的这篇文章主要介绍数据结构中涉及的排序算法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

下面按照课本的分类，做了大致的内排序的归类的图片：

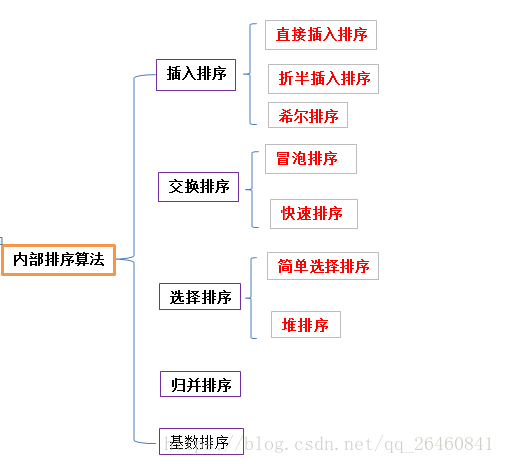
下面我们逐个来实现排序的算法：

一、插入排序算法：
包括：直接插入、折半插入、和希尔排序

其中，插入排序的思想都是一样的，都是以首个待排序的数字作为假设已经有序的序列，然后从已经有序的序列的最后一个位置，从后往前找满这趟比较中元素适合放置的位置。

1. 直接插入插入排序：

/*
直接插入插入排序，假定首个元素有序，
   待插入元素和前面的元素依次大小比较，
   如果满足该元素小于前面一次由后到前的元素，就依次移动元素
   循环判断

   时间复杂度O(n^2) 稳定排序基本有序时时间复杂度为O(n)
*/

void insertSort1(int a[], int n){
    //直接插入排序
    int temp,j;
    for(int i=1;i<n;i++){
        temp = a[i];
        j = i-1;
        while(j>=0 and temp<a[j]){ //逐个元素比较，逐个移动元素 
            a[j+1] = a[j];
            j--;
        }
        a[j+1] = temp;
    } 
}

void insertSort2(int a[], int n){
    int i, j, temp;
    for(i=1;i<n;i++){
        temp = a[i];
        for(j=i-1;temp<a[j] and j>=0;j--){
            a[j+1] = a[j];
        }
        a[j+1] = temp;
    }
}

2. 折半插入排序：

/*折半插入排序
   还是假定首个元素有序，利用折半的思想，在前面有序的序列中
   查找这个元素需要放置的位置，
   找到位置后，一次性移动元素
   最后赋值元素
   时间复杂度 O(n^2) 稳定排序
   折半插入排序，不难看出减少的只是比较元素的次数
   而元素的移动的次数没有改变，
   移动次数依赖于待排序序列的初始状态。
*/

void insertSort(int a[], int n){
    int i,j,low, high, mid, temp;
    for(int i=1;i<n;i++){//外层循环控制循环的趟数
         temp = a[i];
         low = 0;   // 每次循环都是low都是0 
         high = i - 1;  //最大值都是，该元素的前一个元素（有序元素的最大值下标)
         while(low<=high){     //low>high退出 
             //折半判断
            mid = (low+high) / 2;
            if(a[mid] > temp) high = mid - 1;
            else low = mid + 1;
         } 
         //退出后，high+1就是目标位置   high + 1  == low
         for(j=i-1;j>=high+1;j--){
             a[j+1] = a[j];
         } 
         a[high+1] = temp;
    }
}

3. 希尔排序：

/*
希尔排序：
   又叫缩小增量排序，假设步长为d
   从第一个开始，取第d个元素，重复到最后 =>得到子序列
   对子序列进行直接插入排序
   第二趟，d = d / 2;
   重复上面的操作
   直到d = 1为止（d==1时，就是基本有序的序列的直接插入排序）

   直接插入排序适合基本有序的情况，希尔排序的每趟排序
   都会使整个序列更加有序，等整个序列基本有序了
   在进行一趟直接插入排序，使排序的效率更加高效。
   时间复杂度O(n^2) 不稳定排序

    在n属于某个特定范围的时候，时间复杂度为O(n^1.3)
*/

void ShellSort(int a[], int n){
    int d = 1, temp, j;
    while(d>=1){//控制趟数
        for(int i=d;i<n;i+=d){   //这里不能取等号 
            //第0个元素假设有序
            temp = a[i];
            j = i - d;
            while(j>=0 and temp<a[j]){
                a[j+d] = a[j];
                j-=d;
            } 
            a[j+d] = temp;
        } 
        d = d / 2;
    }
}

二、交换排序：

其思想：利用循环遍历，从前往后依次比较，记录每趟排序的最小值的位置，然后本次循环完毕以后，交换最小元素位置到本次排序的最终的位置。

//冒泡排序快速排序
/*
   冒泡排序：
       关键字比较，如果大，则立即交换；
       大的元素往后放，并且一旦确定了本次循环判断中的最大元素，
       将该最大值放入最后的（也是最终的位置）后，下一趟排序，不再与之比较
       最坏情况下的时间复杂度是O(n^2)，平均时间复杂度也是O(n^2) 最好情况下的事件复杂度是O(n)
       稳定排序算法
       每一趟排序都会将一个元素放置到最终的位置上。
*/

void bubbleSort(int a[], int n){
    int temp;
    bool flag = false;
    for(int i=n-1;i>=0;i--){//外层循环始终都是控制趟数
        for(int j=1;j<=i;j++){
            if(a[j-1] > a[j]){
                //这里使用a[j-1]是因为，循环中j<=i,始终比较的是相邻两个元素，故而最大值应该是取到i,故从0开始
                temp = a[j];
                a[j] = a[j-1];
                a[j-1] = temp;
                flag = true;
            }
         } 
         if(flag==false){
             //说明从第一趟开始就没有需要交换的，也就是从小到大排序好了的，所以直接退出
             return; 
         }
    }
}

/*
   快速排序：
       待排序序列，越接近无序，算法的效率越高。逆序情况下的最坏时间复杂度为O(n^2)
       平均时间复杂度为O(nlog2^n)
       空间复杂度为O(log2^n),对应的是栈的深度。它所需要的辅助空间比前面的几类排序算法大。
       快速排序是内部排序中，算法的平均性能最优的排序算法。
       不稳定的排序
       每趟排序的基准元素，放置在其最终的位置上。
*/
方法一：来源天勤辅导书

void quickSort(int a[], int low, int high){
    int temp, i=low, j=high;
    if(low<high){
        temp = a[low];
        while(i!=j){
            while(j>i and a[j]>=temp) --j;
            if(i<j){
            //    cout<<"a["<<i<<"]="<<a[i]<<"||a["<<j<<"]="<<a[j]<<endl;
                a[i] = a[j];
                i++;
            }
            while(j>i and a[i] <= temp) i++;
            if(i<j){
            //    cout<<"a["<<i<<"]="<<a[i]<<"||a["<<j<<"]="<<a[j]<<endl;
                a[j] = a[i];
                j--; 
            }
        }
        a[i] = temp;//当i==j时，表示该趟循环结束，此时i的位置来划分最大最小值 
        quickSort(a, low, i-1);
        quickSort(a, i+1, high);
    }
}

方法二：来源于王道辅导书

//第一次划分也就是第一趟的排序过程 
int partition(int a[], int low, int high){
    int temp = a[low];//第一个元素为划分的轴值 ，对序列进行划分 
    while(low<high){
        while(low<high and a[high]>=temp) high--;
        a[low] = a[high];
        while(low<high and a[low]<=temp) low++;
        a[high] = a[low]; 
    }
    a[low] = temp;
    return low;
} 
void QuickSort(int a[], int low, int high){
    if(low<high){
        int pos = partition(a, low, high);
        QuickSort(a, low, pos - 1);
        QuickSort(a, pos + 1, high);
    }
}

三、选择排序

选择排序，顾名思义也就是每趟排序的过程中挑选满足条件的数据进行排列。（这里我们均默认是升序排列）

如：简单选择排序，先假定第一个比较的数字是最小的，

然后，循环依次和后面的元素的数值进行比较，如果发现还有比假设值还小的数字，记录下标位置

然后在本次循环结束后，发现记录的下标的位置和假定的最小值的下标的位置不同就进行数值的交换操作。

//简单选择排序堆排序
/*
   简单选择排序：
       主要在于“选择”二字。也是最简单的排序算法
       从头到尾顺序扫描序列，找出最小值，和该趟中第一个关键字进行交换
       重复

       时间复杂度始终是O(n^2) 比较的次数和序列的初始状态无关，始终是n(n+1)/2
       不稳定的排序算法
*/

void selectSort(int a[] , int n){
    int temp,min;
    for(int i=0;i<n-1;i++){
        min = i;//记录最小值的下标 
        for(int j=i+1;j<n;j++){
            if(a[j]<a[min]){
                min = j;  //这里记录下标，而不直接交换，有利于减少交换的次数，提高代码运行的效率 
            }
        }
        if(min!=i){
            swap(a[i], a[min]);//C++自带函数 
        }
    }
}

/*
   堆排序： 不稳定的排序算法
       采用完全二叉树的逻辑来编写代码，在实际的编程中用的是数组结构。
       并没有使用完全二叉树来实现建堆、堆调整、删除和排序操作
       不稳定

   将元素存储在一维数组中，然后按照二叉树的逻辑来完成对一维数组中数据的逻辑
   操作上的比较。
   当然也包括建堆、插入结点、删除结点、排序等相关的操作都是以二叉树的逻辑理解
   操作还是在一维数组中。

   堆排序在最坏情况下的时间复杂度是O(nlog2^n) ; 空间复杂度是O(1)，在所有的
   事件复杂度为 O(nlog2^n)的排序算法中，是最小的。
   堆排序适合关键字很多的情况，典型的例子是从10 000个关键字中选择出前10个最小的。
   如果关键字比较少，不建议使用堆排序。
*/
建堆（大根堆）
/*
   层序成堆 a[] = {53,17,78,9,45,65,87,32};

原始序列 53
               /
           17 78
           / /
         9 45 65 87
      /
   32
   排序后 87
/
           45 78
           / /
32 17 65 53
       /
      9
*/

void AdjustDown(int a[], int k, int len){
    a[0] = a[k];
    for(int i=2*k;i<=len;i*=2){
        if(i<len and a[i]<a[i+1]){  //根结点的左右子树中，比较出最大的一个值 
            i++; 
        }
        if(a[0]>=a[i]){
            break;      //说明根大，没有必要比较 
        } else{
            a[k] = a[i];
            k = i;           //因为k始终需要在最后放入临时空间a[0]中的值，故而需要时刻追踪调换后的位置在哪里。 
        } 
    }
    a[k] = a[0];
}

/*
@int a[] a[0]不存储元素，用来在比较的时候暂存数据
*/

void buildMaxHeap(int a[] , int len){
    for(int i=len/2;i>0;i--){              //从[i/2] ~ 1 反复调整堆 
        AdjustDown(a, i, len);   //从最后一个叶子结点的双亲结点开始判断，直到到根结点 
    }
    //从最底层的叶子结点的双亲结点处就开始边压栈边后退，直到根结点。 
}

/*
   操作一：堆排序
       思想：
           输出堆顶元素(也就是最大元素), 然后将堆底元素送入堆顶，此时根结点必然不满足大根堆的
           性质，然后向下调整=>大根堆
           如此循环，再次输出堆顶元素，直到堆中只有一个元素为止。
*/

void heapSort(int a[], int len){
    buildMaxHeap(a, len);//由于是排序算法，所以建堆放在这里比较合适，不用用户自己去调用 
    for(int i=len;i>1;i--){
        cout<<a[1]<<" ";
        swap(a[i], a[1]);
        AdjustDown(a, 1, i-1);
    }
}

/*
   操作二：删除
       思想：
           删除元素，一般而言我们删除的都是我们的堆顶的元素（最大或者最小值）
           所以和上面的排序输出有些类似。
           堆顶元素和最后一个元素进行交换，然后由于破坏了堆的性质，需要进行向下调整的操作。
*/

int HeapDel(int a[], int len){
    int temp = 0;
    buildMaxHeap(a, len);//由于是排序算法，所以建堆放在这里比较合适，不用用户自己去调用 
    for(int i=len;i>1;i--){
        if(i==len){
            //首次操作
            temp = a[1];
            swap(a[i], a[1]); 
        }
        AdjustDown(a, 1, i-1);
    }
    
    //这里需要递归调用向下调整的原因是，我们需要完成大根堆的完整调整。 
    return temp;
}

/*
   操作三：插入
       思想：
           新插入的结点放在堆的末端(数组结构的必然结果)
           然后再对这个结点进行向上调整

*/

//最后一个元素，已经加入了最后一个位置   k 也是元素的个数 (不算a[0]的临时变量结点)
void AdjustUp(int a[], int k){
    a[0] = a[k];
    int i = k / 2;
    while(i>0 and a[i]<a[0]){
        a[k] = a[i];
        k = i;           //和前面的类似，这里用来跟踪交换后的插入结点的位置
        i = k / 2; 
    } 
    a[k] = a[0];
}

void insertHeap(int a[], int len, int n){
    buildMaxHeap(a, len);//先建立大根堆， 然后插入元素 
    //为了模拟，我们不妨定义数组中没有存入数据的是0来占用空间
    a[9] = n;  //在逻辑的最底层插入100节点。
    //调用向上调整函数就可以了
    AdjustUp(a, len+1);//插入了一个元素，长度加一 
}

注：下面是测试用的main函数：
int main(void){
   int a[] = {0,53,17,78,9,45,65,87,32, 0,0,0,0,0};
   buildMaxHeap(a, 8);
   for(int i=0;i<=8;i++){
       cout<<a[i]<<" ";
   }
   cout<<endl;
   cout<<HeapDel(a, 8)<<endl;
   heapSort(a, 8);
   cout<<endl;
   insertHeap(a, 8, 100);//插入100
   for(int i=0;i<=9;i++){
       cout<<a[i]<<" ";
   }
   return 1;
}