1、规约操作

Eigen provides several reduction methods such as: minCoeff() , maxCoeff() , sum() , prod() , trace() *, norm() *, squaredNorm() *, all() , and any() . All reduction operations can be done matrix-wise, column-wise or row-wise . Usage example:

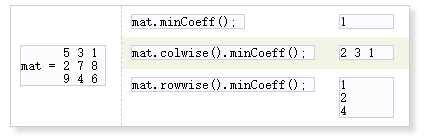
2、最值与索引

可以取到最值与最值的索引。
按行或列取最值时，只能取到行或列的最值组成列或者行，不能取到行或列最值的索引。

#include<Eigen/Core>
#include<iostream>
#include <vector>
using namespace std;
using namespace Eigen;

int test_min_max()
{
	MatrixXd::Index maxRow, maxCol;
	MatrixXd::Index minRow, minCol;
	MatrixXd mMat(4, 4);
	mMat << 11, 10, 13, 15,
		3, 24, 56, 1,
		2, 12, 45, 0,
		8, 5, 6, 4;
	double min = mMat.minCoeff(&minRow, &minCol);
	double max = mMat.maxCoeff(&maxRow, &maxCol);
	cout << "Max = n" << max << endl;
	cout << "Min = n" << min << endl;
	cout << "minRow = " << minRow << "minCol = " << minCol << endl;
	cout << "maxRow = " << maxRow << "maxCol = " << maxCol << endl;
	return 0;
}
 
void test_reduction()
{
	Eigen::MatrixXf mat(2, 4);
	mat << 1, 2, 6, 9,
		3, 1, 7, 2;
	std::cout << "mat: " << std::endl
		<< mat << std::endl;
	std::cout << "Column's maximum: " << std::endl
		<< mat.colwise().maxCoeff() << std::endl;

}

void test_find_max_index()
{
	Eigen::MatrixXf mat(2, 4);
	mat << 1, 2, 6, 9,
		3, 1, 7, 2;
	int i, j, k;
	mat.maxCoeff(&i, &j);
	VectorXf maxindex(mat.rows());
	for (int m = 0; m < mat.rows(); m++)
	{
		VectorXf tmp = mat.row(m);
		tmp.maxCoeff(&k);
		maxindex(m) = k;
	}
	
	std::cout << "The corresponding vector is: " << std::endl;
	std::cout <<i << "t" << j << "n" << maxindex << std::endl;

}

int main()
{
	//test_min_max();
	//test_reduction();
	test_find_max_index();
 
    
    return 0;
}

3、按索引取值 Array of indices

void test_array_of_index()
{
	std::vector<int> ind{ 4,2,5,5,3 };
	MatrixXi A = MatrixXi::Random(4, 6);
	cout << "Initial matrix A:n" << A << "nn";
	cout << "A(all,ind):n" << A(all, ind) << "nn";
}

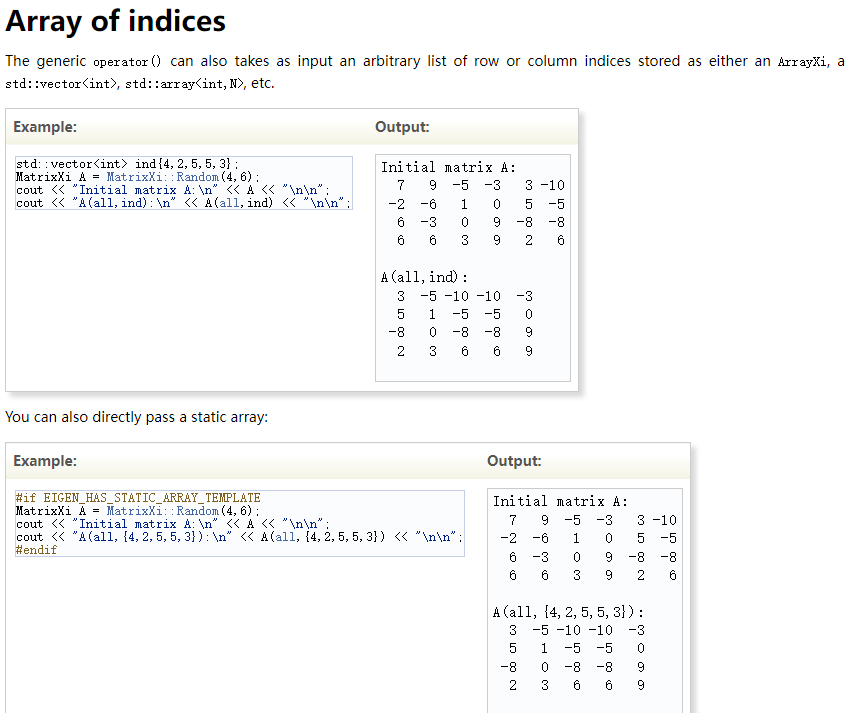
这个功能很好，可是我用的那个Eigen版本 不认识all，所以只能另想办法。
参考：Slicing and Indexing

4、类似 where的功能，生成mask

void test_matrix()
{
	MatrixXd A(4, 4);
	A << 11, 10, 13, 15,
		3, 24, 56, 1,
		2, 12, 2, 0,
		8, 5, 6, 4;
	MatrixXi indices = (A.array() < 3).cast<int>();
	cout << "indices:n" << indices << "nn";
}

输出结果：

indices:
0 0 0 0
0 0 0 1
1 0 1 1
0 0 0 0

5、reshape 改变形状元素个数不变

比如44变成28，2D变成1D拉平。


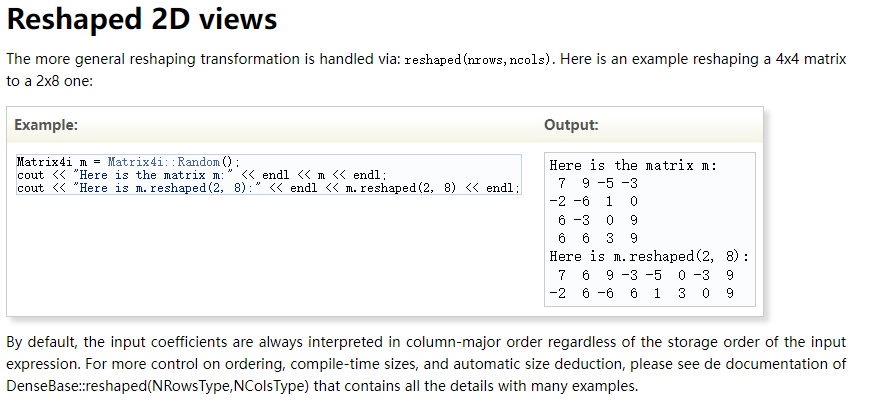
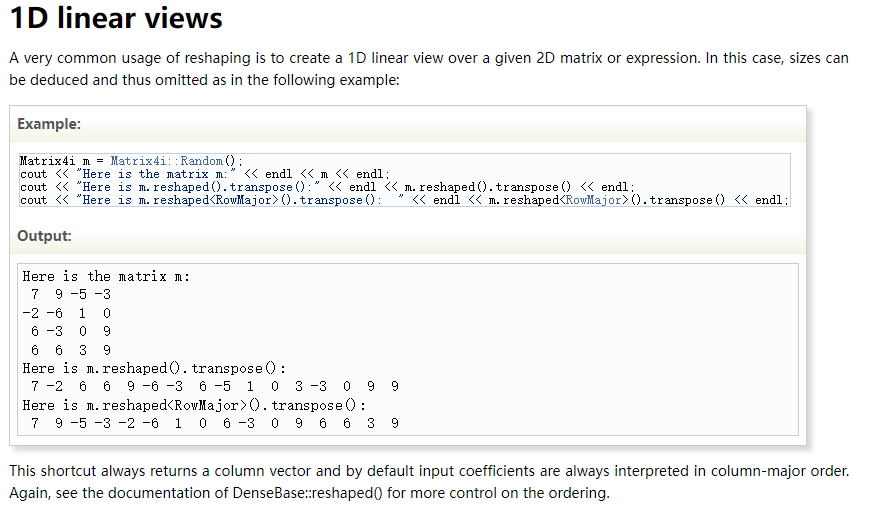
参考：Reshape

6、广播机制

广播是针对vector的，将vector沿行/列重复构建一个matrix，便于后期运算。

int main()
{
  Eigen::MatrixXf mat(2,4);
  Eigen::VectorXf v(2);
  
  mat << 1, 2, 6, 9,
         3, 1, 7, 2;
         
  v << 0,
       1;
       
  //add v to each column of m
  mat.colwise() += v;
  
  std::cout << "Broadcasting result: " << std::endl;
  std::cout << mat << std::endl;
}

输出：

Broadcasting result: 
1 2 6 9
4 2 8 3

注意：对Array类型，*=，/=和/这些操作可以进行行/列级的操作，但不适用于Matrix，因为会与矩阵乘混淆。
结合广播和其他操作
示例：计算矩阵中哪列与目标向量距离最近。

int main()
{
  Eigen::MatrixXf m(2,4);
  Eigen::VectorXf v(2);
  
  m << 1, 23, 6, 9,
       3, 11, 7, 2;
       
  v << 2,
       3;
  MatrixXf::Index index;
  // find nearest neighbour
  (m.colwise() - v).colwise().squaredNorm().minCoeff(&index);
  cout << "Nearest neighbour is column " << index << ":" << endl;
  cout << m.col(index) << endl;
}

输出

Nearest neighbour is column 0:
1
3

参考：归约、迭代器和广播
参考：Reductions
参考：

二维浮点型张量计算矩阵乘积

void test_tensor_matrix_multi(const Eigen::Tensor<float, 2> input1, const Eigen::Tensor<float, 2> input2)
{
    // Compute the traditional matrix product
    Eigen::array<Eigen::IndexPair<float>, 1> product_dims = { Eigen::IndexPair<float>(1, 0) };
    Eigen::Tensor<float, 2> AB = input1.contract(input2, product_dims);
    std::cout << "AB n" << AB << std::endl;
}

最后

以上就是时尚夏天最近收集整理的关于Eigen库学习笔记（五）张量计算1、规约操作2、最值与索引3、按索引取值 Array of indices4、类似 where的功能，生成mask5、reshape 改变形状元素个数不变6、广播机制的全部内容，更多相关Eigen库学习笔记（五）张量计算1、规约操作2、最值与索引3、按索引取值内容请搜索靠谱客的其他文章。