利用Matlab实现单像空间后方交会
空间后方交会的定义为:根据影像覆盖范围内一定数量的分布合理的地面控制点(已知其像点和地面点的坐标),利用共线条件方程,求解影像外方位元素。
- 其原理可以简单地解释为:以单幅影像为基础,从该影像所覆盖地面范围内的若干控制点的已知地面坐标和相应点的像坐标量测值出发,根据共线条件方程,运用最小二乘间接平差方法,求解该影像在航空摄影时刻的外方位元素。
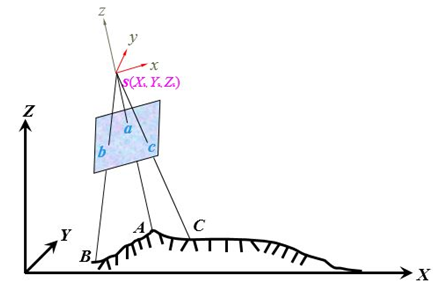
- 已知的四对影像点及其对应的地面点
| 点号 | 像点坐标x(mm) | 像点坐标y(mm) | 地面点坐标X(m) | 地面点坐标Y(m) | 地面点坐标Z(m) |
|---|---|---|---|---|---|
| 1 | -86.15 | -68.99 | 36589.41 | 25273.32 | 2195.17 |
| 2 | -53.40 | 82.21 | 37631.08 | 31324.51 | 728.69 |
| 3 | -14.78 | -76.63 | 39100.97 | 24934.98 | 2386.50 |
| 4 | 10.46 | 64.43 | 40426.54 | 30319.81 | 757.31 |
由于可以将摄影瞬间近似看作垂直摄影情况,可以假设内方位元素已知:
摄影机主距fK=153.24mm;
相片比例尺分母m=50000;
像主点坐标x0=y0=0。
未知数的初始值可以表示为:
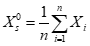
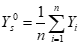
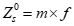
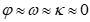
p=4;
q=5;
%定义cell矩阵,存储文件内容
BasicData=cell(p,q);
%以只读方式打开文件
fid=fopen('C:UsersDesktopBasicData.txt','r');
for i=1:p
for j=1:q
%以字符方式读取每个值,遇空格完成每个值的读取
BasicData{i,j}=fscanf(fid,'%s',[1,1]);
end
end
fclose(fid);
for i=1:p
for j=1:q
%将文本格式转为数字格式
BasicData{i,j}=str2double(BasicData{i,j});
end
end
for i=1:4
for j=1:2
BasicData{i,j}=0.001*BasicData{i,j};
end
end
BasicData=cell2mat(BasicData);
%已知的内方位元素%
f=153.24*10^-3;
m=50000;
x0=0;
y0=0;
%确定未知数的近似值
Xs=(BasicData(1,3)+BasicData(2,3)+BasicData(3,3)+BasicData(4,3))/p;
Ys=(BasicData(1,4)+BasicData(2,4)+BasicData(3,4)+BasicData(4,4))/p;
Zs=m*f;
phi=0;
omega=0;
kappa=0;
while(1)
%计算旋转矩阵
R={cos(phi)*cos(kappa)-sin(phi)*sin(omega)*sin(kappa),-cos(phi)*sin(kappa)-sin(phi)*sin(omega)*cos(kappa),-sin(phi)*cos(omega);
cos(omega)*sin(kappa),cos(omega)*cos(kappa),-sin(omega);
sin(phi)*cos(kappa)+cos(phi)*sin(omega)*sin(kappa),-sin(phi)*sin(kappa)+cos(phi)*sin(omega)*cos(kappa),cos(phi)*cos(omega)};
R=cell2mat(R);
%计算像点坐标的近似值
x1(1) = x0-f*(R(1,1)*(BasicData(1,3)-Xs)+ R(2,1)*(BasicData(1,4)-Ys)+ R(3,1)*(BasicData(1,5)-Zs))/(R(1,3)*(BasicData(1,3)-Xs)+ R(2,3)*(BasicData(1,4)-Ys)+ R(3,3)*(BasicData(1,5)-Zs));
y1(1) = y0-f*(R(1,2)*(BasicData(1,3)-Xs)+ R(2,2)*(BasicData(1,4)-Ys)+ R(3,2)*(BasicData(1,5)-Zs))/(R(1,3)*(BasicData(1,3)-Xs)+ R(2,3)*(BasicData(1,4)-Ys)+ R(3,3)*(BasicData(1,5)-Zs));
x1(2) = x0-f*(R(1,1)*(BasicData(2,3)-Xs)+ R(2,1)*(BasicData(2,4)-Ys)+ R(3,1)*(BasicData(2,5)-Zs))/(R(1,3)*(BasicData(2,3)-Xs)+ R(2,3)*(BasicData(2,4)-Ys)+ R(3,3)*(BasicData(2,5)-Zs));
y1(2) = y0-f*(R(1,2)*(BasicData(2,3)-Xs)+ R(2,2)*(BasicData(2,4)-Ys)+ R(3,2)*(BasicData(2,5)-Zs))/(R(1,3)*(BasicData(2,3)-Xs)+ R(2,3)*(BasicData(2,4)-Ys)+ R(3,3)*(BasicData(2,5)-Zs));
x1(3) = x0-f*(R(1,1)*(BasicData(3,3)-Xs)+ R(2,1)*(BasicData(3,4)-Ys)+ R(3,1)*(BasicData(3,5)-Zs))/(R(1,3)*(BasicData(3,3)-Xs)+ R(2,3)*(BasicData(3,4)-Ys)+ R(3,3)*(BasicData(3,5)-Zs));
y1(3) = y0-f*(R(1,2)*(BasicData(3,3)-Xs)+ R(2,2)*(BasicData(3,4)-Ys)+ R(3,2)*(BasicData(3,5)-Zs))/(R(1,3)*(BasicData(3,3)-Xs)+ R(2,3)*(BasicData(3,4)-Ys)+ R(3,3)*(BasicData(3,5)-Zs));
x1(4) = x0-f*(R(1,1)*(BasicData(4,3)-Xs)+ R(2,1)*(BasicData(4,4)-Ys)+ R(3,1)*(BasicData(4,5)-Zs))/(R(1,3)*(BasicData(4,3)-Xs)+ R(2,3)*(BasicData(4,4)-Ys)+ R(3,3)*(BasicData(4,5)-Zs));
y1(4) = y0-f*(R(1,2)*(BasicData(4,3)-Xs)+ R(2,2)*(BasicData(4,4)-Ys)+ R(3,2)*(BasicData(4,5)-Zs))/(R(1,3)*(BasicData(4,3)-Xs)+ R(2,3)*(BasicData(4,4)-Ys)+ R(3,3)*(BasicData(4,5)-Zs));
%计算常数项
for i=1:4
L(2*i-1,1)= BasicData(i,1)-x1(i);
L(2*i,1)=BasicData(i,2)-y1(i);
end
%计算系数矩阵
for i=1:4
A(2*i-1,1)=(R(1,1)*f+R(1,3)*(BasicData(i,1)-x0))/(R(1,3)*(BasicData(i,3)-Xs)+R(2,3)*(BasicData(i,4)-Ys)+R(3,3)*(BasicData(i,5)-Zs));
A(2*i-1,2)=(R(2,1)*f+R(2,3)*(BasicData(i,1)-x0))/(R(1,3)*(BasicData(i,3)-Xs)+R(2,3)*(BasicData(i,4)-Ys)+R(3,3)*(BasicData(i,5)-Zs));
A(2*i-1,3)=(R(3,1)*f+R(3,3)*(BasicData(i,1)-x0))/(R(1,3)*(BasicData(i,3)-Xs)+R(2,3)*(BasicData(i,4)-Ys)+R(3,3)*(BasicData(i,5)-Zs));
A(2*i-1,4)=(BasicData(i,2)-y0)*sin(omega)-cos(omega)*((BasicData(i,1)-x0)*((BasicData(i,1)-x0)*cos(kappa)-(BasicData(i,2)-y0)*sin(kappa))/f+f*cos(kappa));
A(2*i-1,5)=-f*sin(kappa)-(BasicData(i,1)-x0)*((BasicData(i,1)-x0)*sin(kappa)+(BasicData(i,2)-y0)*cos(kappa))/f;
A(2*i-1,6)=(BasicData(i,2)-y0);
A(2*i,1)=(R(1,2)*f+R(1,3)*(BasicData(i,2)-y0))/(R(1,3)*(BasicData(i,3)-Xs)+R(2,3)*(BasicData(i,4)-Ys)+R(3,3)*(BasicData(i,5)-Zs));
A(2*i,2)=(R(2,2)*f+R(2,3)*(BasicData(i,2)-y0))/(R(1,3)*(BasicData(i,3)-Xs)+R(2,3)*(BasicData(i,4)-Ys)+R(3,3)*(BasicData(i,5)-Zs));
A(2*i,3)=(R(3,2)*f+R(3,3)*(BasicData(i,2)-y0))/(R(1,3)*(BasicData(i,3)-Xs)+R(2,3)*(BasicData(i,4)-Ys)+R(3,3)*(BasicData(i,5)-Zs));
A(2*i,4)=-(BasicData(i,1)-x0)*sin(omega)-cos(omega)*((BasicData(i,2)-y0)*((BasicData(i,1)-x0)*cos(kappa)-(BasicData(i,2)-y0)*sin(kappa))/f-f*sin(kappa));
A(2*i,5)=-f*cos(kappa)-(BasicData(i,2)-y0)*((BasicData(i,1)-x0)*sin(kappa)+(BasicData(i,2)-y0)*cos(kappa))/f;
A(2*i,6)=-(BasicData(i,1)-x0);
end
%计算法方程
XX=inv(A'*A)*A'*L;
XN=[Xs;Ys;Zs;phi;omega;kappa]+XX;
Xs=XN(1,1);
Ys=XN(2,1);
Zs=XN(3,1);
phi=XN(4,1);
omega=XN(5,1);
kappa=XN(6,1);
if(abs(XX(4,1))<0.1*pi/10800 && abs(XX(5,1))<0.1*pi/10800 && abs(XX(6,1))<0.1*pi/10800 )
break;
end
end
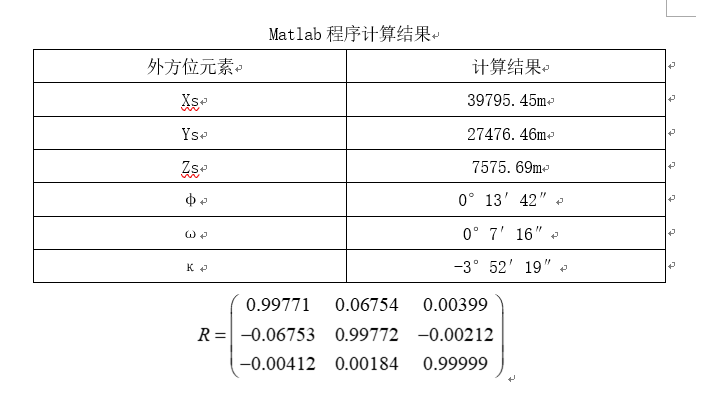
Xs=vpa(XN(1,1),7)
Ys=vpa(XN(2,1),7)
Zs=vpa(XN(3,1),6)
phi=vpa(degrees2dms(rad2deg(XN(4,1))),2)
omega=vpa(degrees2dms(rad2deg(XN(5,1))),2)
kappa=vpa(degrees2dms(rad2deg(XN(6,1))),2)
R
原始数据,BasicData.txt文件内容
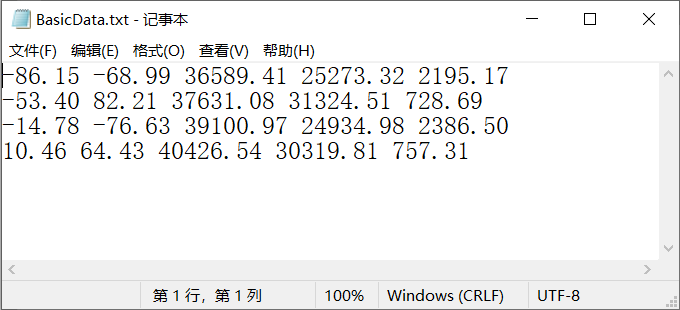
最后
以上就是怕黑芝麻最近收集整理的关于利用Matlab实现单像空间后方交会利用Matlab实现单像空间后方交会的全部内容,更多相关利用Matlab实现单像空间后方交会利用Matlab实现单像空间后方交会内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复