两个向量
x
,
y
∈
R
n
x,y in{Bbb R}^n
x,y∈Rn的内积定义如下:
⟨
x
,
y
⟩
:
=
x
⋅
y
=
∑
i
=
1
n
x
i
y
i
langle x,y rangle := x cdot y = sum_{i=1}^n x_i y_i
⟨x,y⟩:=x⋅y=i=1∑nxiyi
即对两个向量执行对应位一一相乘再求和。
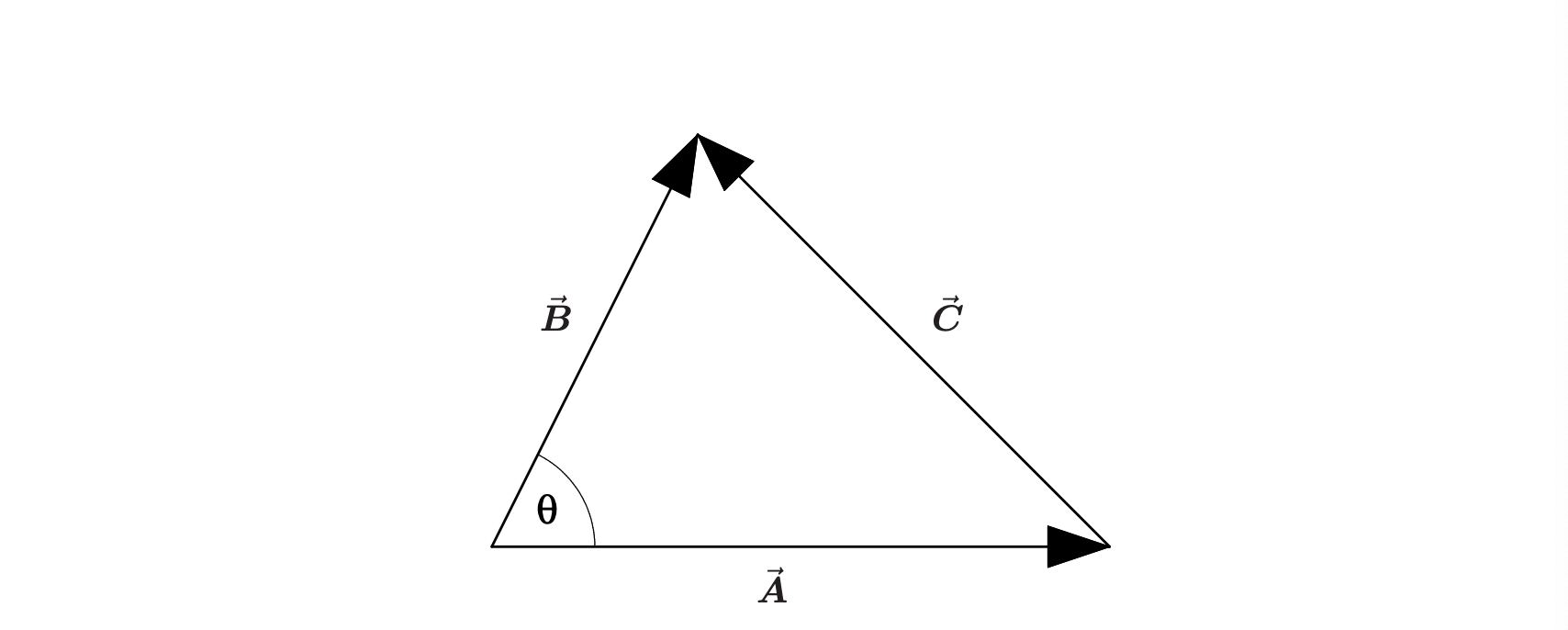
如图,经过证明可以得到,即两个向量的内积(内乘)可以计算两个向量的夹角。
A ⃗ ⋅ B ⃗ = ∣ ∣ A ⃗ ∣ ∣ ∣ ∣ B ⃗ ∣ ∣ c o s θ vec A cdot vec B = ||vec A||||vec B||costheta A⋅B=∣∣A∣∣∣∣B∣∣cosθ
证明过程如下:

参考资料:
- The Geometry of the Dot and Cross Products
最后
以上就是强健中心最近收集整理的关于向量内积的几何意义证明过程的全部内容,更多相关向量内积内容请搜索靠谱客的其他文章。







发表评论 取消回复