浮点数的舍入方案（IEEE标准）

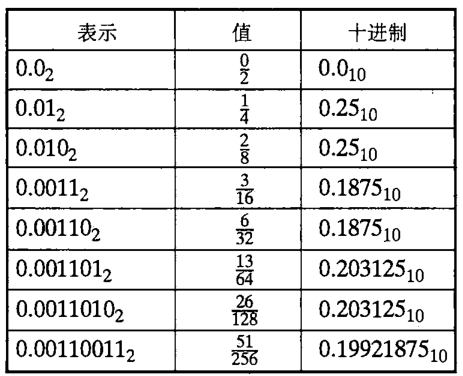
1.浮点数不可能精确表示每一个数的，比如0.2。因此对于值x，我们一般想用一种系统的方法，能够找到最接近的匹配值

2.IEEE规定了4种舍入方案。

向偶数舍入、向零舍入、向上舍入、向下舍入。

系统默认采用   向最接近的值舍入（round-to-nearest）。这是基础，其他三种方式用于计算上下界。

即向最接近的设舍入（round-to-nearest）是一个总称。它具体采用哪一种方式要由具体情况而定。

1）当舍入方式发生分歧时，优先采用向偶数舍入。

无论是10进制数，还是二进制数，只有在数值为中间值时，才会发生纠纷。

例如：1.235，向上是 1.24；向下/向零 1.23。误差相同都是0.005。这时我们优先采用向偶数舍入，即1.24。

          1.245，向上是 1.25；向下/向零 1.24。误差相同都是0.005。这时我们优先采用向偶数舍入，即1.24。

而1.234999，我们保留两位小数时，就没有必要纠结。向上/向偶 1.24   误差为0.0050001；向下/向零 1.23  误差为0.0049999.向下的误差最小，所以系统会采用1.23。

在比如  1.2350001，舍入到1.24的误差值要小于舍入到1.23的误差值，没必要纠结。

2）其余方式，向最近的值舍入。

注意

为什么要在纠结的时候采用向偶数舍入。

采用向上舍入一组数值，会在计算这些值得平均数中引入统计偏差。我们采用这些方式舍入得到的一组数的平均值将比这些数本身的平均值略高一些。

相反，采用向下舍入一组数值，得到的平均值会比本身的平均值略低一些。

向偶数舍入在大多数现实情况中避免了这种统计偏差。因为在50%的时间内，他将向上舍入；在50%De时间内，他将向下舍入。

最后

以上就是称心大地最近收集整理的关于浮点数的舍入方案（IEEE标准）的全部内容，更多相关浮点数内容请搜索靠谱客的其他文章。