参考:https://zhuanlan.zhihu.com/p/22450818?refer=dong5
1、FFT,分析基波的参与时间对傅里叶变换的影响
基波为4个余弦波,用matlab程序控制其参与输入信号的增益。
当增益为1,4基波全时参与时,输入信号为: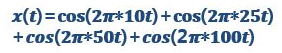
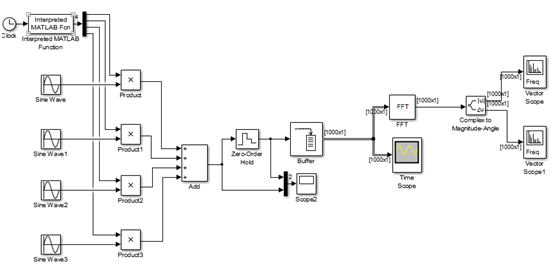
注意:FFT后在Vector Scope显示每帧的频率图时,应设置采样频率,否则,频率计算可能有误!
比如,Buffer设置 overlap不为0时。
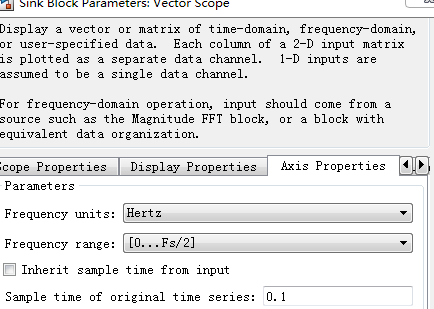
输入信号的控制程序为:
function y=get_a(t)
%根据仿真时间控制输入信号的增益
if(t<0.25)
y(1)=1;
else
y(1)=0;
end
if(t>=0.25&&t<0.5)
y(2)=1;
else
y(2)=0;
end
if(t>=0.5&&t<0.75)
y(3)=1;
else
y(3)=0;
end
if(t>=0.75)
y(4)=1;
else
y(4)=0;
end
三种信号的FFT变换结果如下:
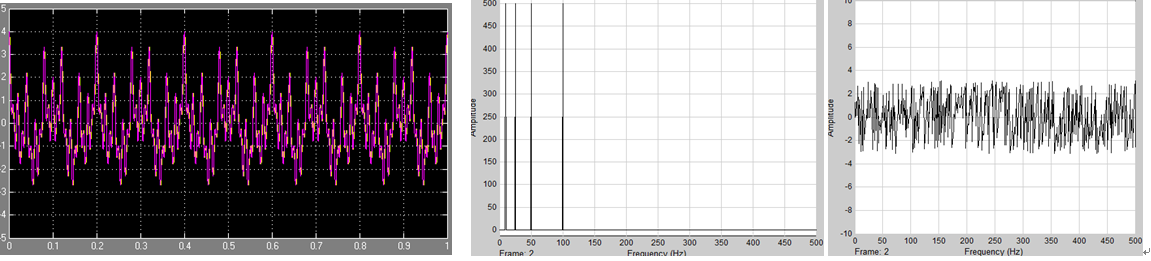

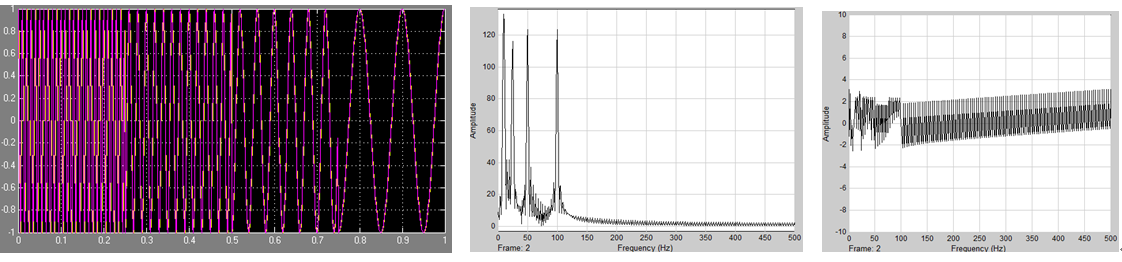
从上图可知,不同的时域信号可能有相同的幅值谱,更多的信息应该隐藏在相位谱中,可是怎么分析相位谱呢???
FFT无法取得基波参与的时间信息。对时域信号加窗进行STFT,是一个方法。
2、STFT 直接用spetrogram()更方便。
参考:https://blog.csdn.net/lvsehaiyang1993/article/details/80583269
Fs = 1000;
t=0:1/Fs:0.249;
y1=cos(2*pi*10*t);
y2=cos(2*pi*20*(t+0.250));
y3=cos(2*pi*50*(t+0.500));
y4=cos(2*pi*100*(t+0.750));
y=[y1,y2,y3,y4];
t=0:1/Fs:0.999;
plot(t',y')
% 将信号lenSignal=1000点划分成长度为window=100个点,使用海明窗加窗,使用noverlap=80个样本重叠,
%估计[100/2+1]=51个频率点,fix((1000-80)/(100-80))=46个时间点
%FFT计算点数nfft=100
spectrogram(y,100,80,100,Fs,'yaxis')
view(-77,72)
shading interp
colorbar off
%[s,f,t,p]=spectrogram(y,100,80,100,Fs);%s:51x46,f:51x1,t:1x46
%spectrogram(...) plots the power spectral density (PSD) estimate for each segment on a surface in a figure window. The plot is created using
%surf(T,F,10*log10(abs(P)));
%axis tight;
%view(0,90);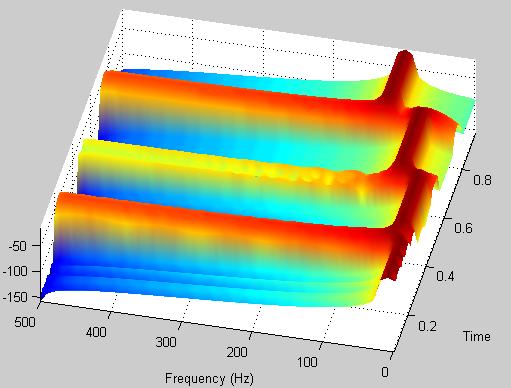
%绘制图谱,对每列t,求最大功率谱密度PSD(dB),标记红色点
[s,f,t,p] = spectrogram(y,100,80,100,Fs);
[q,nd] = max(10*log10(p));
hold on
plot3(t,f(nd),q,'r','linewidth',4)
hold off 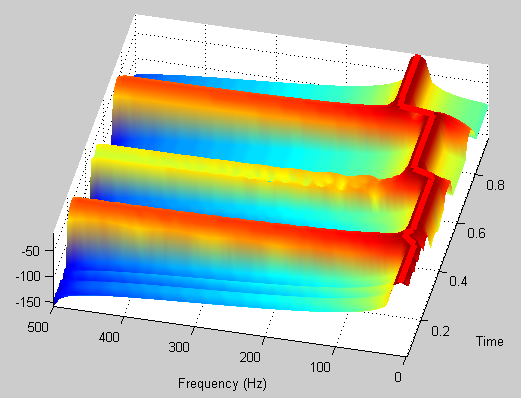
当窗口改大为250时(时间点减少),结果如下,频率分开了,但是时间上模糊了。
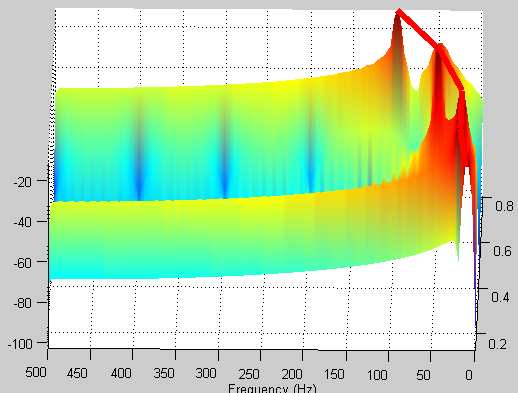
窄窗口时间分辨率高、频率分辨率低,宽窗口时间分辨率低、频率分辨率高。对于时变的非稳态信号,高频适合小窗口,低频适合大窗口。然而STFT的窗口是固定的,在一次STFT中宽度不会变化,所以STFT还是无法满足非稳态信号变化的频率的需求。
奈奎斯特定理(采样定理),采样频率大于信号频率的2倍,才能复现该信号。一般实际应用中保证采样频率为信号最高频率的2.56~4倍。
下面用STFT绘制时频谱图,然后和小波分析的结果进行对比:
t=0:0.001:0.249;
y1=cos(2*pi*10*t);
y2=cos(2*pi*20*(t+0.250));
y3=cos(2*pi*50*(t+0.500));
y4=cos(2*pi*100*(t+0.750));
y=[y1,y2,y3,y4];
%subplot(1,2,1)
figure
plot(y)
Fs = 1000;
% 将信号划分成长度为100个点,使用海明窗加窗,使用80个样本重叠,估计[100/2+1]=51个频率点,不使用默认
%的颜色棒。
%subplot(1,2,2)
%figure
[s,f,t,p]=spectrogram(y,100,80,100,Fs,'yaxis');
surf(t,f,abs(s));
set(gca,'Yscale','log');
set(gca,'ytick',[1:9,10:10:90,100:100:900,1000,2000]);
view(0,90);
%view(-77,72)
shading interp
colorbar off
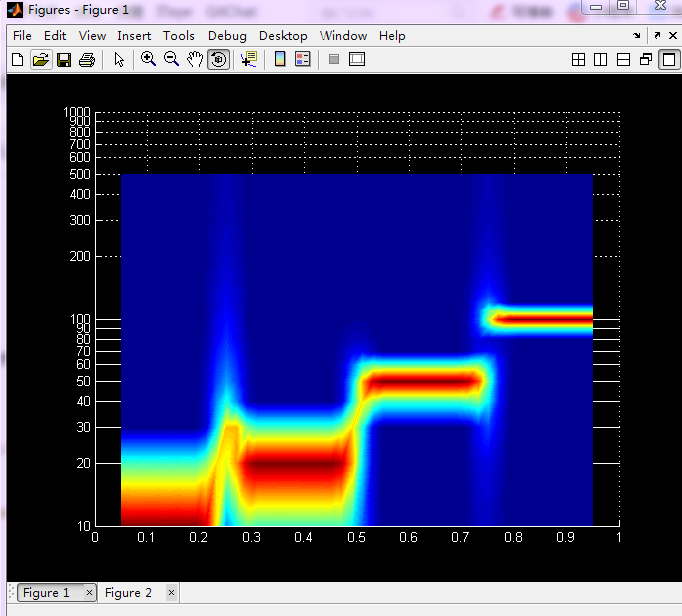
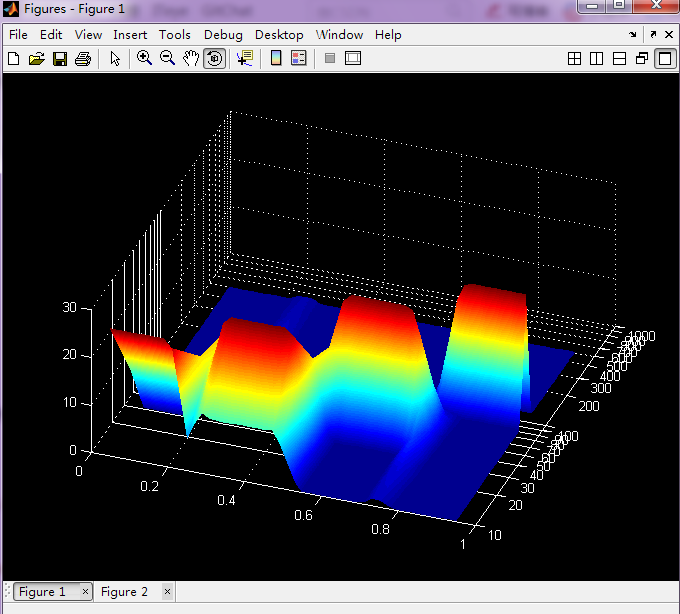
从上图可知,当window和nfft都取100时,频率分辨率很小!
当window和nfft都取200时,频率分辨率增加,但是时间分辨率下降,如下图:
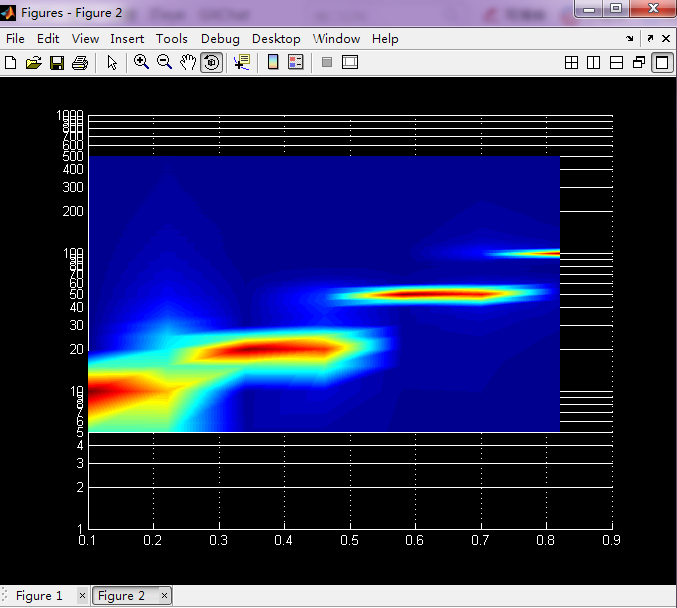
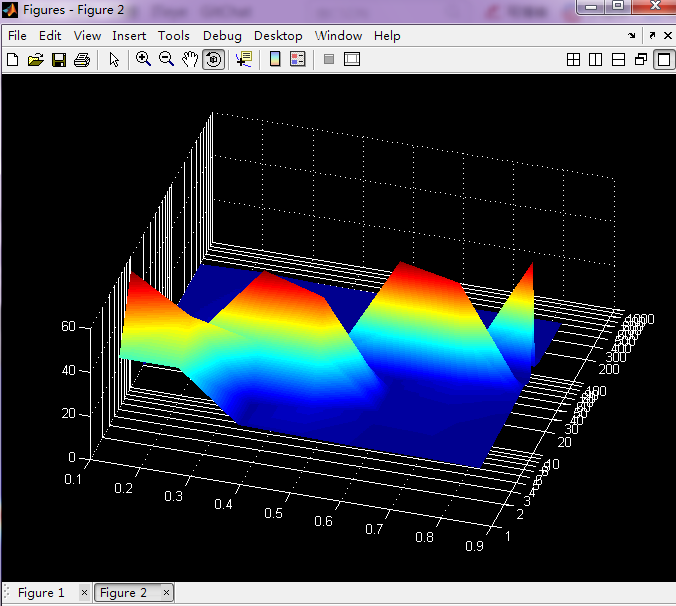
3、小波分析。
Fs = 1000;
t=0:1/Fs:0.249;
y1=cos(2*pi*10*t);
y2=cos(2*pi*20*(t+0.250));
y3=cos(2*pi*50*(t+0.500));
y4=cos(2*pi*100*(t+0.750));
y=[y1,y2,y3,y4];
t=0:1/Fs:0.999;
%figure;
plot(t',y')
xlabel('时间t');
ylabel('信号y(t)');
title('原始信号');
scale=1:200;
cw2=cwt(y,scale,'morl');
%figure;
[X,Y]=meshgrid(t,centfrq('morl')*Fs./scale);%小波的中心频率*采样频率/尺度=》频率
%scal2frq(scale,'morl',1/Fs)=centfrq('morl')*Fs./scale
mesh(X,Y,abs(cw2));
title('小波时频图');
xlabel('时间t(s)');
ylabel('频率(Hz)');
xlim([t(1),t(end)]);
set(gca,'Ylim',[0,max(max(Y))]);
set(gca,'Yscale','log');
set(gca,'ytick',[1:9,10:10:90,100:100:900,1000,2000]);
view(0,90);
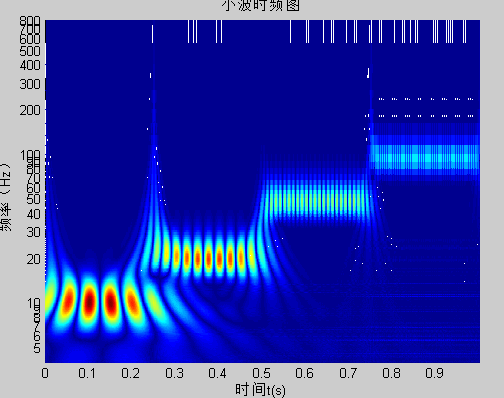
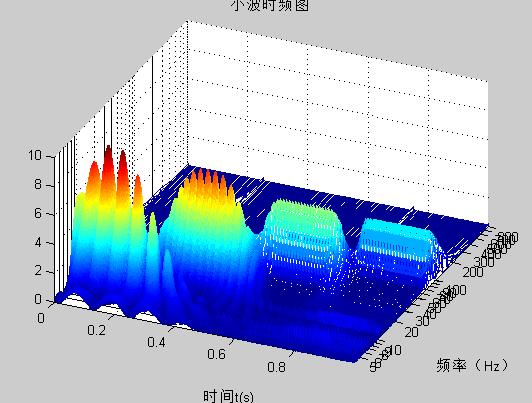
??通常,高频信号持续的时间短,小波的窗口窄,以提高时间分辨率,低频信号持续时间长,小波的窗口宽,以提高频率分辨率。
所以用小波分析,可以满足低频信号高频率分辨率、高频信号高时间分辨率的要求!
最后
以上就是忧伤台灯最近收集整理的关于用simulink分析傅里叶变换、短时傅里叶变换和小波变换的全部内容,更多相关用simulink分析傅里叶变换、短时傅里叶变换和小波变换内容请搜索靠谱客的其他文章。








发表评论 取消回复