使用内置的函数和常量
- 基本函数
- 三角函数
- atan(a/b):根据正切求角度,范围为[ − π 2 , π 2 {-}frac{pi }{2},frac{pi }{2} −2π,2π]
- atan2(a,b):根据a/b正切值和(a,b)所在象限求角度,范围为[ − π , π -pi , pi −π,π]
- 向量、矩阵操作相关
- 解方程、符号表达式相关
- 画图
- 这里是补充
- 内部常数
- 常用内部数学函数
- 数学运算符
- 调用maple
- 数学式的转换
- 复数运算
- 表示集合
- 求集合的交集、并集、差集和补集
- 如何用matlab排序
基本函数
| 函数 | 作用 | 栗子 |
|---|---|---|
| clear | 清除工作区中的所有变量 | |
| clc | 清除命令行中的所有代码 | |
| help 函数名 或 doc 函数名 | 查找函数帮助 | |
| syms | 定义符号变量 | syms x y ; |
| sym(‘f’) | 定义符号表达式 | sym(‘x*y^2’) |
| pi | 圆周率(matlab区分大小写) | π |
| vpa(x,k) | x的数值,保留k位有效数字 | x=vpa(sin(1/3), 2) ⇨x=0.33 |
| real(x) | 求复数x的实部 | x = real(1+2i) ⇨ x = 1 |
| eval() | 字符串转数值 | x = eval(‘5’) ⇨ x = 5 |
| sqrt() | 开根号 | x = sqrt(4) ⇨ x = 2 |
| exp() | 以自然常数e为底的指数函数 | x = exp(2) ⇨ y = e² |
| log() | 以e为底的对数函数 | x = log(exp(1)) ⇨ x = 1 |
| log10() | 以10为底的对数函数 | x = log(10) ⇨ x = 1 |
| abs() | 取绝对值 | x = abs(-1) ⇨ x = 1 |
| mod(m,n) | m对n取余,返回m/n的余数 | x = mod(3,2) ⇨ x = 1 |
三角函数
| 函数 | 作用 | 备注 |
|---|---|---|
| sin()、cos()、tan()、cot() | 三角函数 | x=sin(deg2rad(30)) ⇨x=0.5 |
| rad2deg()、deg2rad() | 弧度转角度、角度转弧度 | x=deg2rad(30) ⇨ x=0.5236 |
| asin()、acos()、 atan()、acot() | 反三角函数,结果为弧度值 | x = asin(0.5) ⇨ x = 0.5236 |
| asind()、acosd()、atand()、acotd() | 反三角函数,结果为角度值 | x = asind(0.5) ⇨ x = 30.0° |
atan(a/b):根据正切求角度,范围为[ − π 2 , π 2 {-}frac{pi }{2},frac{pi }{2} −2π,2π]
atan2(a,b):根据a/b正切值和(a,b)所在象限求角度,范围为[ − π , π -pi , pi −π,π]
rad2deg(atan(sin(deg2rad(45))/cos(deg2rad(45))))%返回45
rad2deg(atan2(sin(deg2rad(135)),cos(deg2rad(135))))% 返回 135
向量、矩阵操作相关
| 函数 | 作用 | 备注 |
|---|---|---|
| 函数 | 作用 | 备注 |
| size(A) | 返回矩阵的行数和列数 | |
| size(C,1) / size(C,2) | 返回矩阵的行数 / 列数 | |
| length(A) 或 max(size(A)) | 返回长度最大的维度的长度 | |
| numel(A) | 返回矩阵元素的总个数 | |
| sum(A) | 返回矩阵所有元素的和 | x = sum([1,2]) ⇨ x = 3 |
| inv(A) | 返回矩阵A的逆 | |
| ndims(A) | 返回矩阵A的维度 | 单个数值、向量和二维矩阵返回值均为2 |
| iscolumn(x) / isrow(x) | 判断是否为列向量 / 行向量 | |
| isvector() / ismatrix() | 判断是否为向量 / 矩阵 | |
| isempty(x) / isscalar() | 判断是否为空向量 /单个数值 | |
| dot(a, b) | 向量a点乘b,点积 | |
| cross(a, b) | 向量a叉乘b,叉乘 | |
| repmat(A,m,n) | 通过将A复制m行n列,返回m*n的矩阵 |
A = [1]%例
U = repmat(A,2,2)

解方程、符号表达式相关
| 函数 | 作用 | 备注 |
|---|---|---|
| simplify(f) | 化简公式f | |
| collect(f) | 合并同类项 | |
| expand(f) | 展开公式 | |
| horner(f) | 将乘法嵌套 | 数值计算性能较好 |
| factor(f) | 因式分解 | |
| pretty(f) | 相对直观地显示公式 | 复杂的公式不行 |
| [n,d] = numden(f) | 通分,返回分母n,分子d | 通分前会先自动化简表达式 |
- 以解三角函数为例
% 解三角函数方程
clear;clc;
syms theta1
x=0;y=670;L1=260;L2=260;L3=150;
% 方法一:复杂
eqn = 2*x*(L1+L3)*cos(theta1)+2*y*(L1+L3)*sin(theta1) == x^2+y^2+(L1+L3)^2-L2^2;
theta1 = solve(eqn,theta1);
theta1 = real(theta1)
% 方法二:推荐,简单
eqn = 2*x*(L1+L3)*cos(theta1)+2*y*(L1+L3)*sin(theta1) == x^2+y^2+(L1+L3)^2-L2^2;
theta1 = solve(eqn,theta1,'Real',true)
画图
| figure() | 创建画布 | 备注 |
|---|---|---|
| clf() | 清空画布的内容 | |
| set() | 设置图形对象属性,如画布名字、在屏幕上的位置等 | |
| plot(X,Y) | 创建 Y 中数据对 X 中对应值的二维线图 | |
| plot3() | 绘制三维图像 | 数值计算性能较好 |
| xlabel()、ylabel() | 横轴、纵轴标签 | |
| xlim()、ylim() | 横轴、纵轴范围 | 复杂的公式不行 |
| text() | 标注图线名称 | 通分前会先自动化简表达式 |
| title() | 添加图题 | |
| hold on / hold off | 不刷新画布(在一张画布画多张图) / 刷新画布 | |
| legend() | 添加图例 | |
| grid on / grid off | 打开 / 关闭网格线 | |
| grid minor | 打开最小网格线 | |
| box on / box off | 打开 / 关闭 右、上边框线 | |
| save() | 保存工作区变量 | |
| saveas() / imwrite() | 保存图片 | |
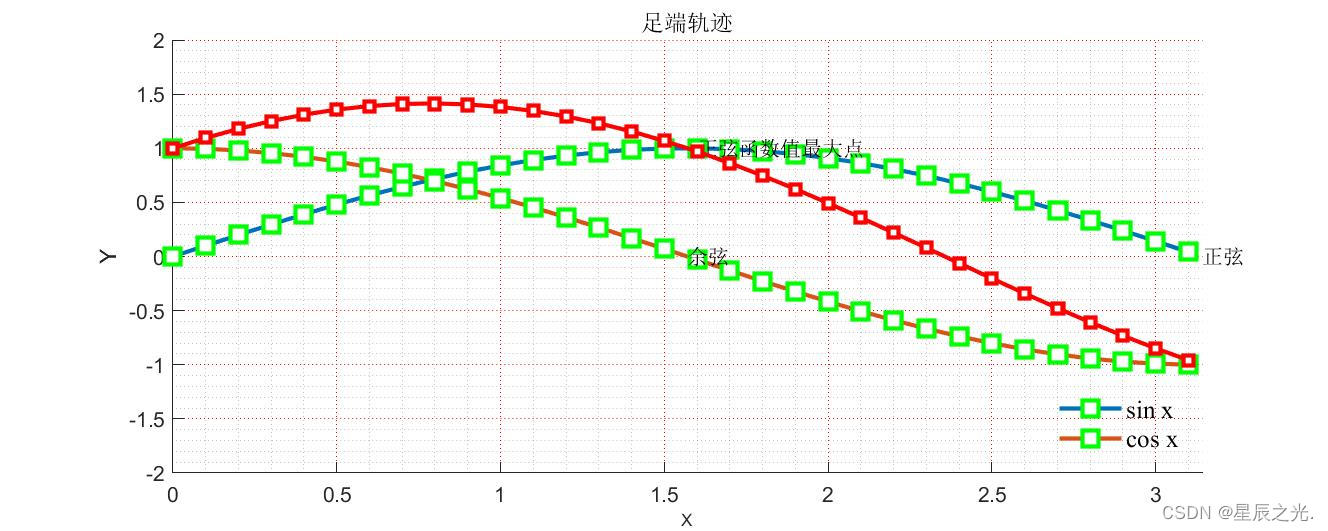
| 这里有一个例子: |
% 例子
clc;clear;close all;
x=0:0.1:pi; y=sin(x); z=cos(x);
h1 = figure(1); % 创建画布,画布编号为1
set(h1,'name','图1');
set(h1,'pos',[350 250 850 340]);
% 线宽、数据点标记形状、标记填充颜色、标记框线颜色、标记大小
p1 = plot(x,y,x,z,'linewidth',2,'Marker','s','MarkerFaceColor','w','MarkerEdgeColor','g','MarkerSize',10);
xlabel('X');ylabel('Y');
xlim([0,pi]);ylim([-2,2]);
set(get(gca,'XLabel'),'FontSize',8); % 设置X轴数字大小
title('足端轨迹');
text(pi,0,'正弦'); text(pi/2,0,'余弦');
[a,b] = max(y);
text(x(b),a,'正弦函数值最大点');
hold on;
p2 = plot(x,y+z,'r','linewidth',2,'Marker','s','MarkerFaceColor','w'); % 线颜色、线形
legend('sin x','cos x','Fontsize',12,'Location','southeast','fontname','Times');
legend('boxoff'); % 关闭图例外框
grid on;
set(gca,'GridLineStyle',':','GridColor','r','GridAlpha',1); % ':':网格线虚线;'-':网格线实线
grid minor;
box off;
save('a.mat','a','b')
saveas(h1,'三角函数.jpg'); % 保存图片
% clf(1); % 清空画布的内容
这里是补充
内部常数
pi 圆周率
exp(1) 自然对数的底数e
i 或j 虚数单位
Inf或 inf 无穷大
常用内部数学函数
| 指数函数 | exp(x) | 以e为底数 |
|---|---|---|
| 对数函数 | log(x) | 自然对数,即以e为底数的对数 |
| log10(x) | 常用对数,即以10为底数的对数 | |
| log2(x) | 以2为底数的x的对数 | |
| 开方函数 | sqrt(x) | 表示x的算术平方根 |
| 绝对值函数 | abs(x) | 表示实数的绝对值以及复数的模 |
| 三角函数 (自变量的单位为弧度) | sin(x) | 正弦函数 |
| cos(x) | 余弦函数 | |
| tan(x) | 正切函数 | |
| cot(x) | 余切函数 | |
| sec(x) | 正割函数 | |
| csc(x) | 余割函数 | |
| 反三角函数 | asin(x) | 反正弦函数 |
| acos(x) | 反余弦函数 | |
| atan(x) | 反正切函数 | |
| acot(x) | 反余切函数 | |
| asec(x) | 反正割函数 | |
| acsc(x) | 反余割函数 | |
| 双曲函数 | sinh(x) | 双曲正弦函数 |
| cosh(x) | 双曲余弦函数 | |
| tanh(x) | 双曲正切函数 | |
| coth(x) | 双曲余切函数 | |
| sech(x) | 双曲正割函数 | |
| csch(x) | 双曲余割函数 | |
| 反双曲函数 | asinh(x) | 反双曲正弦函数 |
| acosh(x) | 反双曲余弦函数 | |
| atanh(x) | 反双曲正切函数 | |
| acoth(x) | 反双曲余切函数 | |
| asech(x) | 反双曲正割函数 | |
| acsch(x) | 反双曲余割函数 | |
| 求角度函数 | atan2(y,x) | 以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度,范围为( , ] |
| 数论函数 | gcd(a,b) | 两个整数的最大公约数 |
| lcm(a,b) | 两个整数的最小公倍数 | |
| 排列组合函数 | factorial(n) | 阶乘函数,表示n的阶乘 |
| 复数函数 | real(z) | 实部函数 |
| imag(z) | 虚部函数 | |
| abs(z) | 求复数z的模 | |
| angle(z) | 求复数z的辐角,其范围是( , ] | |
| conj(z) | 求复数z的共轭复数 | |
| 求整函数与截尾函数 | ceil(x) | 表示大于或等于实数x的最小整数 |
| floor(x) | 表示小于或等于实数x的最大整数 | |
| round(x) | 最接近x的整数 | |
| 最大、最小函数 | max([a,b,c,...]) | 求最大数 |
| min([a,b,c,..]) | 求最小数 | |
| 符号函数 | sign(x) | |
| 对数函数 | log(x) | 自然对数,即以e为底数的对数 |
| log10(x) | 常用对数,即以10为底数的对数 | |
| log2(x) | 以2为底数的x的对数 | |
| 开方函数 | sqrt(x) | 表示x的算术平方根 |
| 绝对值函数 | abs(x) | 表示实数的绝对值以及复数的模 |
| 三角函数 (自变量的单位为弧度) | sin(x) | 正弦函数 |
| cos(x) | 余弦函数 | |
| tan(x) | 正切函数 | |
| cot(x) | 余切函数 | |
| sec(x) | 正割函数 | |
| csc(x) | 余割函数 | |
| 反三角函数 | asin(x) | 反正弦函数 |
| acos(x) | 反余弦函数 | |
| atan(x) | 反正切函数 | |
| acot(x) | 反余切函数 | |
| asec(x) | 反正割函数 | |
| acsc(x) | 反余割函数 | |
| 双曲函数 | sinh(x) | 双曲正弦函数 |
| cosh(x) | 双曲余弦函数 | |
| tanh(x) | 双曲正切函数 | |
| coth(x) | 双曲余切函数 | |
| sech(x) | 双曲正割函数 | |
| csch(x) | 双曲余割函数 | |
| 反双曲函数 | asinh(x) | 反双曲正弦函数 |
| acosh(x) | 反双曲余弦函数 | |
| atanh(x) | 反双曲正切函数 | |
| acoth(x) | 反双曲余切函数 | |
| asech(x) | 反双曲正割函数 | |
| acsch(x) | 反双曲余割函数 | |
| 求角度函数 | atan2(y,x) | 以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度,范围为( , ] |
| 数论函数 | gcd(a,b) | 两个整数的最大公约数 |
| lcm(a,b) | 两个整数的最小公倍数 | |
| 排列组合函数 | factorial(n) | 阶乘函数,表示n的阶乘 |
| 复数函数 | real(z) | 实部函数 |
| imag(z) | 虚部函数 | |
| abs(z) | 求复数z的模 | |
| angle(z) | 求复数z的辐角,其范围是( , ] | |
| conj(z) | 求复数z的共轭复数 | |
| 求整函数与截尾函数 | ceil(x) | 表示大于或等于实数x的最小整数 |
| floor(x) | 表示小于或等于实数x的最大整数 | |
| round(x) | 最接近x的整数 | |
| 最大、最小函数 | max([a,b,c,...]) | 求最大数 |
| min([a,b,c,..]) | 求最小数 | |
| 符号函数 | sign(x) |
数学运算符
| a+b | 加法 | a./b | 数组右除 |
|---|---|---|---|
| a-b | 减法 | a.b | 数组左除 |
| a*b | 矩阵乘法 | a^b | 矩阵乘方 |
| a.*b | 数组乘法 | a.^b | 数组乘方 |
| a/b | 矩阵右除 | -a | 负号 |
| ab | 矩阵左除 | ' | 共轭转置 |
| .' | 一般转置 |
| == | 等于 |
|---|---|
| < | 小于 |
| > | 大于 |
| <= | 小于或等于 |
| >= | 大于或等于 |
| ~= | 不等于 |
调用maple
| maple(’denom(f)’) | 提取分式f的分母 |
|---|---|
| maple(’numer(f)’) | 提取分式f的分子 |
| maple(’normal(f)’ ) | 把分式f的分子与分母约分成最简形式 |
| maple(’expand(f)’) | 把分式f的分子展开,分母不变且被看成单项。 |
| maple(’factor(f)’) | 把分式f的分母和分子因式分解,并进行约分。 |
如何用Matlab进行因式分解
syms 表达式中包含的变量 factor(表达式)
如何用Matlab展开
syms 表达式中包含的变量 expand(表达式)
如何用Matlab进行化简
syms 表达式中包含的变量 simplify(表达式)
如何用Matlab合并同类项
syms 表达式中包含的变量 collect(表达式,指定的变量)
数学式的转换
调用Maple中数学式的转换命令,调用格式如下:
maple(‘Maple的数学式转换命令’)
即:maple(‘convert(表达式,form)’) 将表达式转换成form的表示方式
maple(‘convert(表达式,form, x)’) 指定变量为x,将依赖于变量x的函数转换成form的表示方式(此指令仅对form为exp与sincos的转换式有用)
如何用Matlab进行变量替换
syms 表达式和代换式中包含的所有变量 subs(表达式,要替换的变量或式子,代换式)
复数运算
| a+b*i 或 a +b*j | 表示复数a+bi 或 a+bj |
|---|---|
| real(z) | 求复数z的实部 |
| imag(z) | 求复数z的虚部 |
| abs(z) | 求复数z的模 |
| angle(z) | 求复数z的辐角, |
| conj(z) | 求复数z的共轭复数 |
| exp(z) | 复数的指数函数,表示e^z |
表示集合
[a, b, c,…] 表示由a, b, c,…组成的集合 (注意:元素之间也可用空格隔开)
unique(A) 表示集合A的最小等效集合(每个元素只出现一次)
也可调用maple的命令,格式如下:
maple(‘{a, b, c,…}’) 表示由a, b, c,…组成的集合
下列命令可以生成特殊的集合:
maple(‘{seq(f(i),i=n…m)}’) 生成集合{f(n), f(n+1), f(n+2), … , f(m)}
求集合的交集、并集、差集和补集
| union(A,B) | 求集合A和B的并集 |
|---|---|
| intersect(A,B) | 求集合A和B的交集 |
| setdiff(A,B) | 求集合A和B的差集A-B |
| setdiff(U,A) | 求集合A关于全集U的补集 |
我们也可以调用Maple的相应功能,调用方法如下:
maple('用Maple求集合的交集、并集、差集和补集的命令 ')
具体地说,共有下列几个调用命令:
maple( ‘A union B’ ) 求集合A和B的并集
maple( 'A intersect B ’ ) 求集合A和B的交集
maple('A minus B ’ ) 求差集A-B
maple( '全集I minus A ’ ) 求集合A关于全集I的补集
如何用matlab排序
sort(v) 将向量v的元素从小到大排列(升序排列)
最后
以上就是仁爱康乃馨最近收集整理的关于【Matlab入门】使用内置的函数和常量基本函数三角函数向量、矩阵操作相关解方程、符号表达式相关画图这里是补充的全部内容,更多相关【Matlab入门】使用内置内容请搜索靠谱客的其他文章。








发表评论 取消回复