前言
本来是打算写关于矩阵的一些东西,但是弄了一半,发现需要的线代知识有点多,直接讲相关的使用,就太直白了,可能根本无法理解是什么意思,如果讲线代的知识,就感觉和该系列的文不太符,所以直接弃了那部分,打算之后讲到其他例程的时候,夹杂在其中进行,本篇就对MATLAB中常用的数学函数做一些记录。
三角函数
三角函数这个就真的是很常用很常用了,特别是做数字信号处理的时候,经常做混频用,当然其他的领域也常用到,不过对其他领域不太熟,所以就不举例子了
以下的表格是一些三角函数的函数名,及其说明,然后拿几个大家比较熟悉的出来演示:
| 函数名 | 说明 |
|---|---|
| sin | 正弦函数 |
| sinh | 双曲正弦函数 |
| asin | 反正弦函数,返回弧度 |
| asinh | 反双曲正弦函数 |
| cos | 余弦函数 |
| cosh | 双曲余弦函数 |
| acos | 反余弦函数,返回弧度 |
| acosh | 反双曲余弦函数 |
| tan | 正切函数 |
| tanh | 双曲正切函数 |
| atan | 反正切函数,返回弧度 |
| atanh | 反双曲正切函数 |
| asech | 反双曲正割函数 |
| cot | 余切函数 |
| coth | 双曲余切函数 |
| acot | 反余切函数,返回弧度 |
| acoth | 反双曲余切函数 |
| asind | 反正弦函数,返回角度 |
| acosd | 反余弦函数,返回角度 |
| atand | 反正切函数,返回角度 |
| acotd | 反余切函数,返回角度 |
简单使用:
%第一部分
x=0:0.01:4*pi;
y1=cos(x);
y2=sin(x);
figure(1);
plot(x,y1,'r',x,y2,'g')
%第二部分
x=-5*pi:pi/27:5*pi;
y1=sin(x);
y2=cos(x);
y3=tan(x);
figure(2);
plot(x,y1,'r',x,y2,'g',x,y3,'b');%r:红色 g:绿色 b:蓝色
运行的效果:
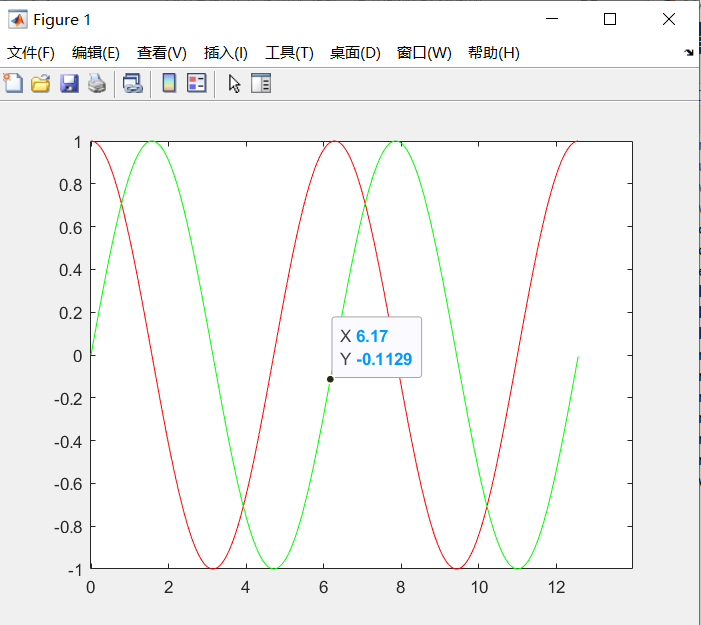
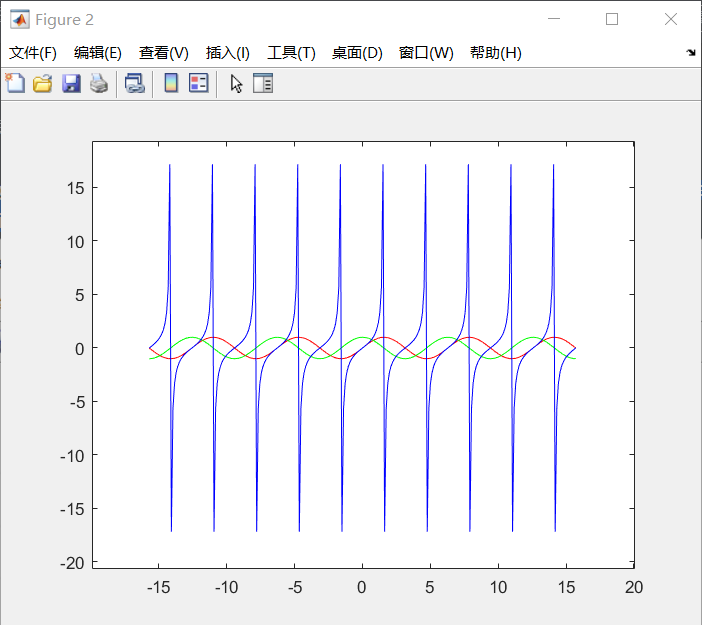
实例应用:
题:已知三角形的三条边,分别长2、3、4,求解长度2和4的两条边的夹角。
解题方案:直接通过计算夹角的余弦值,然后直接通过反余弦得到该角的值,当然也肯定还可以有其他的方法,有需要可以自行挖掘。
解题程序:
x=2;y=4;z=3;
cos_alpha=(x^2+y^2-z^2)/(2*x*y)
alpha_r=acos(cos_alpha)%弧度
alpha_d=alpha_r*180/pi%弧度转角度
alpha_d2=acosd(cos_alpha)%直接得角度
解题结果:

指数和对数函数
这两个函数的话,我也不知道咋说,现在印象里只记得弄功率谱的时候可以用下,其他的近来也没使用上,反正很重要就对了。
常用的指数和对数函数如下表,expm和logm就是用于矩阵的,和exp、log很好区别,加了个m(matrix):
| 函数名 | 说明 |
|---|---|
| exp | 指数函数 |
| log | 自然函数,即对数函数 |
| log2 | 以2为底的对数,分割浮点数 |
| log10 | 以10为底的对数 |
| nextpow2 | 下一个以2为底的更高次幂 |
| pow2 | 以2为底的幂和比例浮点数 |
| expm | 矩阵指数函数 |
| logm | 矩阵对数函数 |
简单使用:
%程序1
a=2;
e=exp(a)
l=log(a)
l2=log2(a)
l10=log10(a)
np=nextpow2(a)
p=pow2(a)
s=sqrt(a)
结果太长,就直接复制数值过来比对了:
e =
7.3891
l =
0.6931
l2 =
1
l10 =
0.3010
np =
1
p =
4
s =
1.4142
%程序2
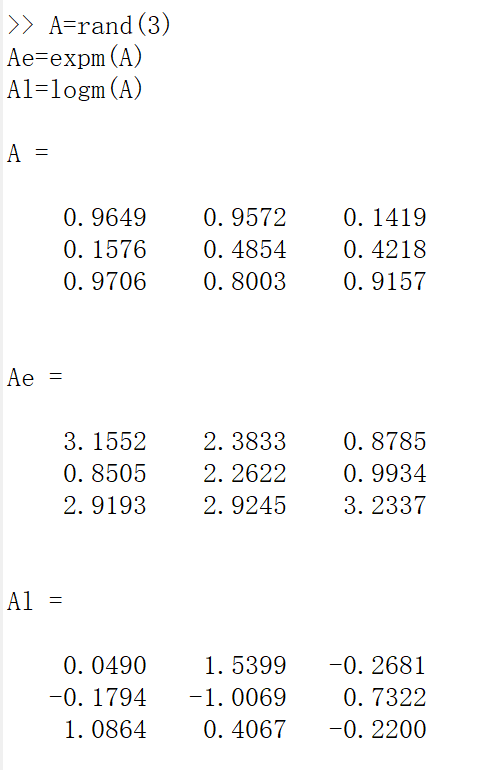
A=rand(3)
Ae=expm(A)
Al=logm(A)
结果如下:
复数处理函数
关于复数的处理函数,这个最近就比较深刻了,做工程的时候,用得蛮多的,在MATLAB里面除了一些变换以及直接赋值可以得到复数外,还可以直接用complex函数构造一个复数,对复数可以操作的函数,在下表中的展示:
| 函数名 | 说明 |
|---|---|
| abs | 绝对值、复数的模 |
| angle | 相位角 |
| complex | 构造复数 |
| conj | 复共轭 |
| cplxpair | 在复共轭对中加入有序数 |
| imag | 复数虚部 |
| real | 复数实部 |
| isreal | 判断数组是否为实数 |
| unwrap | 不展开相位角 |
简单使用:
%程序
a=complex(3,4)
a_r=real(a)
a_i=imag(a)
a_abs=abs(a)
a_ang=angle(a)
a_c=conj(a)
还是一样,直接复制数据结果:
a =
3.0000 + 4.0000i
a_r =
3
a_i =
4
a_abs =
5
a_ang =
0.9273
a_c =
3.0000 - 4.0000i
离散函数
离散函数就如名字一样,是离散的效果,通过离散函数绘制离散的数据,可以得到冲击状和阶梯状的图,分别是stem和stairs,这两个就没必要列表了,直接看下使用的效果吧。
简单使用:
x=0:0.1:2;
figure(1);
stem(exp(-x.^2),'fill','r-.');%'fill' 'r-.' 填充红色,并以-.与横坐标对齐
figure(2);
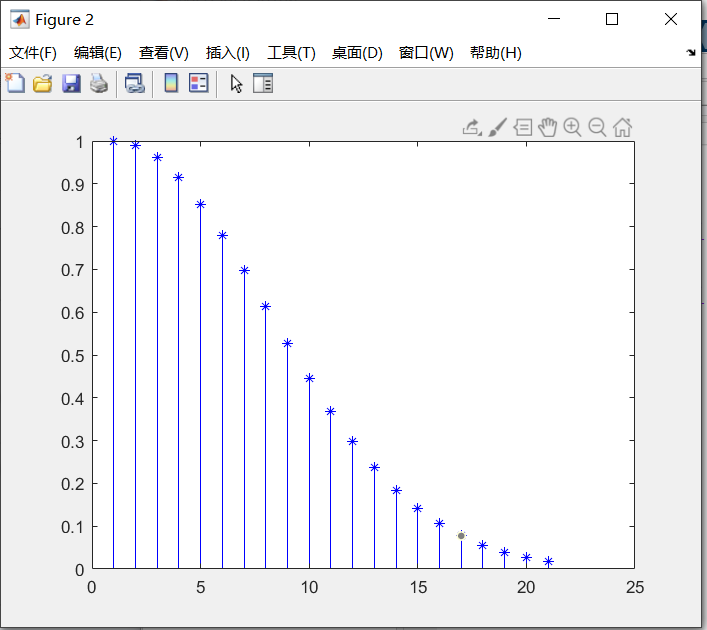
stem(exp(-x.^2),'fill','b-*');%'fill' 'b-*' 填充蓝色,并以-*与横坐标对齐
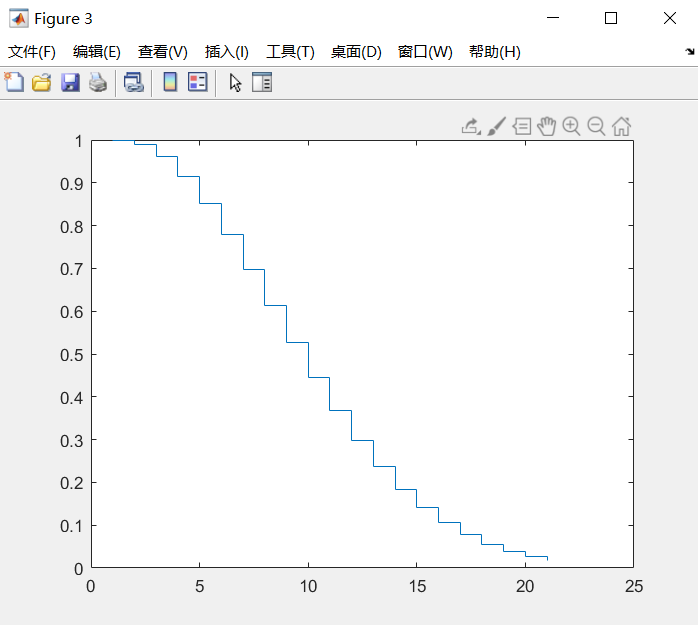
figure(3);
stairs(exp(-x.^2));%绘制阶梯图
运行结果:
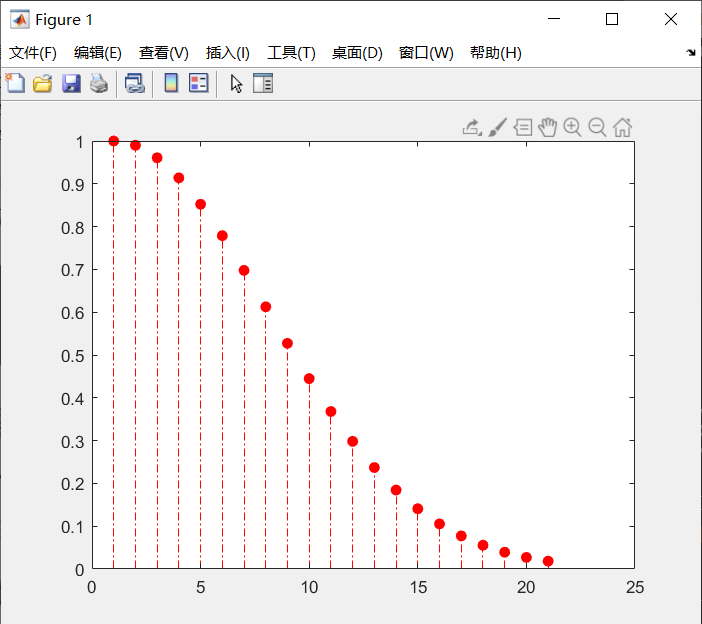
特殊数学函数
这部分的就是真的特殊了,如果没啥需要的话,可以直接结束本篇的阅读了,想看的话,就往下慢慢阅读。
通过特殊的函数可以实现坐标系的变换、绘制特殊函数曲线、特定积分运算以及误差处理等等,部分特殊数学函数如下表:
| 函数名 | 说明 |
|---|---|
| airy | 艾里函数 |
| besselj | 第一类贝塞尔*(Bessel)*函数 |
| bessely | 第二类贝塞尔*(Bessel)*函数 |
| besselh | 第三类贝塞尔*(Bessel)*函数 |
| besseli | 第一类变形的贝塞尔*(Bessel)*函数 |
| besselk | 第二类改进的贝塞尔*(Bessel)*函数 |
| beta | Beta函数 |
| betainc | 不完全Beta函数 |
| betaln | 对数Beta函数 |
| ellipj | 雅可比矩阵(Jacobi)椭圆函数 |
| ellipke | 完全椭圆函数 |
| cart2pol | 直角坐标变极坐标 |
| cart2sph | 直角坐标变球坐标 |
| erf | 误差函数 |
| erfinv | 误差函数的逆函数 |
| erfc | 余误差函数 |
| erfcinv | 余误差函数的逆函数 |
| erfcx | 互补误差函数(erfcx(x)=exp(x^2)*erfc(x)) |
| expint | 指数积分函数 |
| gamma | Gamma函数 |
| gammainc | 不完全Gamma函数 |
| gammaln | 对数Gamma函数 |
| psi | Psi函数 |
| legendre | Legendre函数 |
| pol2cart | 极主标变直角坐标 |
| sph2cart | 球坐标变直角坐标 |
直接来个看着让人懵逼的图,代码就不分析了,有点印象就好,用到了再去help吧~
%特殊函数简单例程
[X,Y]=meshgrid(-10:0.02:2,-3:0.02:3);
BH=besselh(0,1,X+i*Y);
contour(X,Y,abs(BH),0:0.2:10);hold on
contour(X,Y,(180/pi)*angle(BH),-180:10:180);hold off
format rat
B=beta((0:10),3)
BC=betainc(0.5,(0:10),3)
PSI=psi(1,2)
结果:



坐标转换的也再来个吧:
%坐标转换
r=1;
theta=linspace(0,pi);
phi=linspace(0,2*pi);
[tt,pp]=meshgrid(theta,phi);
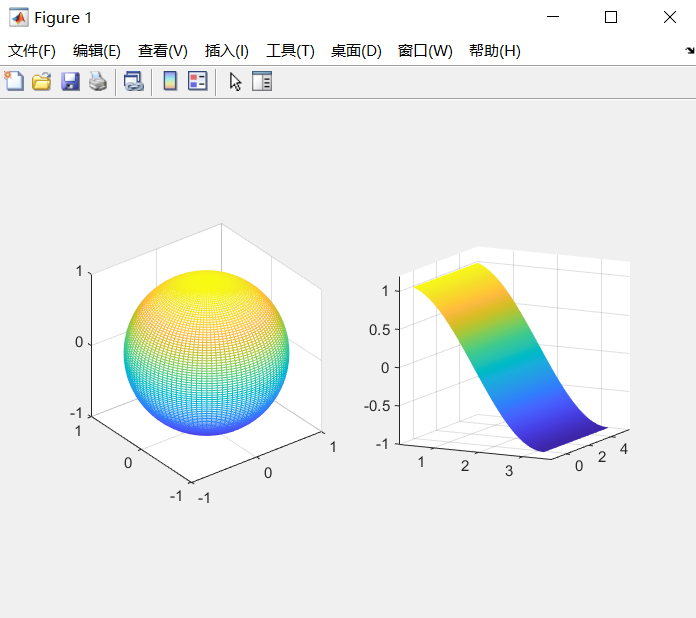
[x,y,z]=sph2cart(pp,pi/2-tt,r);
subplot(121);
mesh(x,y,z);
axis square%设为方形
shading flat%不使用高级着色
subplot(122);
mesh(tt,pp,z);
shading flat%不使用高级着色
axis square%设为方形
运行结果:
本次的记录到此结束,关于图形的相关函数如果不懂的可以自己先help进行了解,后续也会针对图形的函数进行记录分享。
-更多精彩等你发现-
最后
以上就是爱听歌月亮最近收集整理的关于Matlab中的那些数学函数前言三角函数指数和对数函数复数处理函数离散函数特殊数学函数的全部内容,更多相关Matlab中内容请搜索靠谱客的其他文章。








发表评论 取消回复