一、什么是决策树的剪枝

对比日常生活中，环卫工人在大街上给生长茂密的树进行枝叶的修剪。在机器学习的决策树算法中，有对应的剪枝算法。将比较复杂的决策树，化简为较为简单的版本，并且不损失算法的性能。

二、为什么要剪枝

剪枝是决策树算法应对过拟合的一种策略，因为在学习过程中，决策树根据训练样本进行拟合，生成了针对于训练数据集精确性极高的模型。但是训练数据集，不可避免是一种有偏的数据。所以我们为了提高决策树的泛化性能，采取了剪枝的策略。使得决策树不那么对于训练数据精确分类，从而适应任何数据。

三、剪枝的基本策略

剪枝的策略可以分为预剪枝和后剪枝两种。

预剪枝：对每个结点划分前先进行估计，若当前结点的划分不能带来决策树的泛化性能的提升，则停止划分，并标记为叶结点。

后剪枝：现从训练集生成一棵完整的决策树，然后自底向上对非叶子结点进行考察，若该结点对应的子树用叶结点能带来决策树泛化性能的提升，则将该子树替换为叶结点。

四、预剪枝和后剪枝的优缺点

        1、预剪枝

            优点：思想简单，算法高效，可以降低过拟合风险，减少训练时间。

            缺点：可能存在欠拟合的风险。

         2、后剪枝

            优点：欠拟合风险小，泛化能力优于预剪枝。

            缺点：相较于预剪枝，训练开销大。

五、奥卡姆剃刀定律

奥卡姆剃刀是一种思想，在效果相同，性能一致的情况下，模型越简单越好。在简直过程中，若复杂的决策树和简答的决策树的性能相同则优先选择结构简单的决策树。

六、预剪枝和后剪枝的具体实现

1.数据准备

数据依然采用的是集美大学计算机工程学院acm比赛校选的数据，其中每列的属性分别是成绩、用时、年级、奖项。并对其离散化。

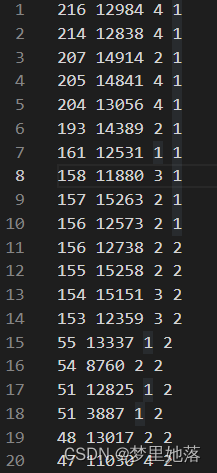
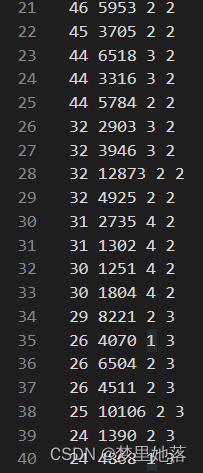
 其中将成绩、用时、年级分为4个等级，数字越大，分别代表成绩越高，用时越长，年级越高。奖项分为3个等级，1等奖，2等奖，3等奖。

2.划分数据集

与以往不同的是，这次我们将数据集分为两部分，一部分是大于最优特征的特征值的，一部分是小于目标特征的特征值的。

#按照给定区间划分数据集
def splitDataSet_bydata_font(dataSet,axis,value):# 待划分的数据集 划分数据集的特征 比较的特征值
    retDataSet_font=[]
    if isinstance(dataSet,list) ==False:  #判断dataSet是不是列表
        dataSet=dataSet.tolist() #转化列表
    for featVec in dataSet:#遍历每一行
        if featVec[axis] <=value: 
            reducedFeatVec=featVec[:axis]
            reducedFeatVec.extend(featVec[axis:])#放列表中的元素
            retDataSet_font.append(reducedFeatVec)#把整个列表放入
    return retDataSet_font


#按照给定特征区间划分数据集
def splitDataSet_bydata_back(dataSet,axis,value):# 待划分的数据集 划分数据集的特征 比较的特征值
    retDataSet_back=[]
    if isinstance(dataSet,list) ==False:
        dataSet=dataSet.tolist()
    for featVec in dataSet:#遍历每一行
        if featVec[axis] >value: 
            reducedFeatVec=featVec[:axis]
            reducedFeatVec.extend(featVec[axis:])#放列表中的元素
            retDataSet_back.append(reducedFeatVec)#把整个列表放入
    return retDataSet_back

3.判断最优值

通过计算各特征的信息增益，将信息增益最大的特征及最优的特征值当作划分的标准。

#判断最优值
def chooseBestData(dataset):
    num=len(dataset[0])-1 #除掉类别
    baseEnt=calcShannonEnt(dataset)#信息熵
    print("原本的信息熵",baseEnt)
    bestGain=0.0 
    bestFeature=-1
    bestdata=0
    for i in range(num):#0 1 2
        #创建唯一的分类标签列表
        featlist=[example[i] for example in dataset]#取该行数据的第“ i ”位元素
        for value in featlist:
            newEnt=0.0
            #计算每种划分方式的信息熵
            subDataSet_font=splitDataSet_bydata_font(dataset,i,value)
            subDataSet_back=splitDataSet_bydata_back(dataset,i,value)
            
            prob_font=len(subDataSet_font)/float(len(dataset))#计算比例
            prob_back=len(subDataSet_back)/float(len(dataset))

            newEnt=prob_font*calcShannonEnt(subDataSet_font)+prob_back*calcShannonEnt(subDataSet_back)
            #计算信息增益
            inforGain=baseEnt-newEnt
            #计算最好的信息熵
            if (inforGain>bestGain):
                print("当前信息熵增益为:",inforGain,"当前最优特征为",i,"划分值为:",value)
                bestGain=inforGain
                bestFeature=i
                bestdata=value
    return bestFeature,bestdata

 上面的输出结果是第一次划分的所显示的结果。我们发现最佳的特征是成绩，最好的划分值是1。

4. 投票决策

 在构建决策树，可能会出现这一种情况，如果数据集已经处理了所有的属性，但是类标签依然不是唯一的。在这种情况下，我们通常会采用多数表决的方法决定叶子节点的分类。

#投票分类
def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys():classCount[vote]=0
        classCount[vote]+=1
    sortedClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    print(sortedClassCount)
    return sortedClassCount[0][0] #返回出现次数最多的分类

5.创建树

创建出还未进行剪枝的树进行观察

def createTree(dataSet,labels):
    #类别完全相同则停止划分
    classList=[example[-1] for example in dataSet]
    if classList.count(classList[0])==len(classList):
        #print("发生了类别完全相同",classList[0])
        return classList[0]
    #遍历完所有特征时返回出现次数最多的类别
    if len(dataSet[0])==1:
        return majorityCnt(classList)

    bestFeat,bestData=chooseBestData(dataSet)
    bestFeatLabel=labels[bestFeat]
    myTree={bestFeatLabel:{}}
    #分支的多少和循环次数有关
    listJudge=["<="+str(bestData),">="+str(bestData)]
    subLabels=labels[:] #复制一份
    print(bestFeat,bestData)
    newDataSet_font=splitDataSet_bydata_font(dataSet,bestFeat,bestData)
    newDataSet_back=splitDataSet_bydata_back(dataSet,bestFeat,bestData)
    print(newDataSet_font)
    if(newDataSet_font!=[] and bestFeat!=-1):
        myTree[bestFeatLabel][listJudge[0]]=createTree(newDataSet_font,subLabels)
    if(newDataSet_back!=[] and bestFeat!=-1):
        myTree[bestFeatLabel][listJudge[1]]=createTree(newDataSet_back,subLabels)

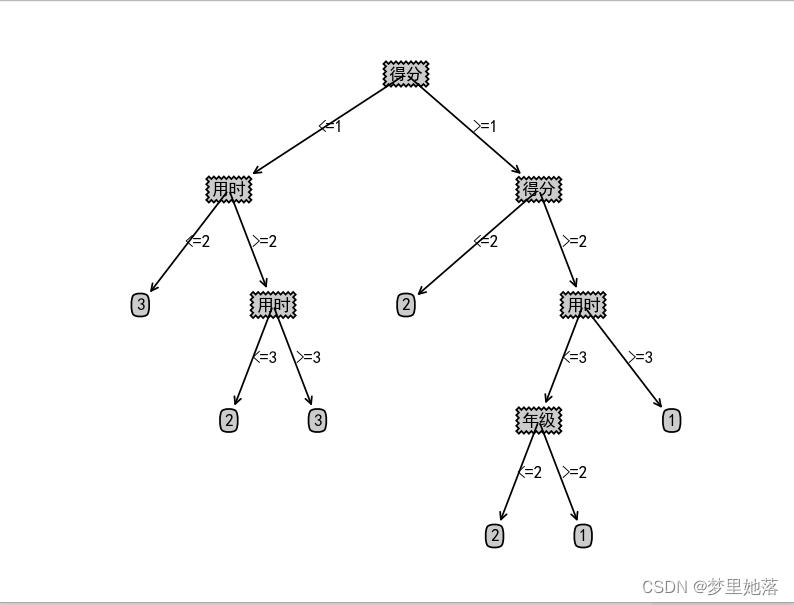
    return myTree

将树的结构可视化的代码与上次的博客相同，这里就不列出了。树可视化为

6.进行预减枝

预减枝有多种方法，我在本文中采用的是限定树的深度进行预剪枝。

def createTree(dataSet,labels,depth):

    classList=[example[-1] for example in dataSet]
    #达到指定深度停止划分
    if depth==0:
        return majorityCnt(classList)
    #类别完全相同则停止划分
    if classList.count(classList[0])==len(classList):
        return classList[0]
    #遍历完所有特征时返回出现次数最多的类别
    if len(dataSet[0])==1:
        return majorityCnt(classList)

    bestFeat,bestData=chooseBestData(dataSet)
    bestFeatLabel=labels[bestFeat]
    myTree={bestFeatLabel:{}}
    #分支的多少和循环次数有关
    listJudge=["<="+str(bestData),">"+str(bestData)]
    subLabels=labels[:] #复制一份
    print(bestFeat,bestData)
    newDataSet_font=splitDataSet_bydata_font(dataSet,bestFeat,bestData)
    newDataSet_back=splitDataSet_bydata_back(dataSet,bestFeat,bestData)
    print(newDataSet_font)
    if(newDataSet_font!=[] and bestFeat!=-1):
        newDepth=depth-1
        myTree[bestFeatLabel][listJudge[0]]=createTree(newDataSet_font,subLabels,newDepth)
    if(newDataSet_back!=[] and bestFeat!=-1):
        newDepth=depth-1
        myTree[bestFeatLabel][listJudge[1]]=createTree(newDataSet_back,subLabels,newDepth)

    return myTree


if __name__ == '__main__':
    mytree=createTree(data,labels,3)
    createPlot(mytree)

效果如下

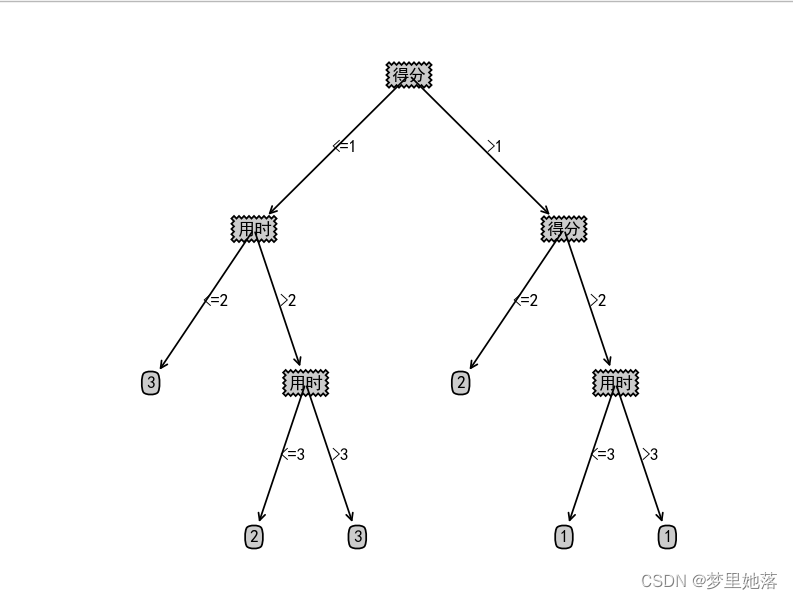
我们发现，将深度设置为3时，年级的分类就被剪枝去掉了。存在欠拟合的风险。

7.错误记录

（1）报错： 

AttributeError: 'dict' object has no attribute 'iteritems'

         原因：

python3中已经没有 “iteritems” 这个属性了，现在属性是：“ items ” 。

        解决办法：

将代码中的iteritems 修改为：items

最后

以上就是隐形钢笔为你收集整理的机器学习--决策树二（预剪枝和后剪枝）一、什么是决策树的剪枝二、为什么要剪枝三、剪枝的基本策略四、预剪枝和后剪枝的优缺点五、奥卡姆剃刀定律六、预剪枝和后剪枝的具体实现的全部内容，希望文章能够帮你解决机器学习--决策树二（预剪枝和后剪枝）一、什么是决策树的剪枝二、为什么要剪枝三、剪枝的基本策略四、预剪枝和后剪枝的优缺点五、奥卡姆剃刀定律六、预剪枝和后剪枝的具体实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。