LSTM结构理解与python实现LSTM结构理解与python实现

57 阅读 0 评论 38 点赞

我是靠谱客的博主内向导师，最近开发中收集的这篇文章主要介绍LSTM结构理解与python实现LSTM结构理解与python实现，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

LSTM结构理解与python实现

上篇博客中提到，简单的RNN结构求解过程中易发生梯度消失或梯度爆炸问题，从而使得较长时间的序列依赖问题无法得到解决，其中一种越来越广泛使用的解决方法就是 Long Short Term Memory network (LSTM)。本文对LSTM做一个简单的介绍，并用python实现单隐藏层LSTM。

参考资料：

理解LSTM： http://colah.github.io/posts/2015-08-Understanding-LSTMs/ (一个非常棒的博客，对LSTM基本结构的讲解浅显易懂)
LSTM前向和后向传播：http://arunmallya.github.io/writeups/nn/lstm/index.html#/ (公式简单明了)
Alex Graves的博士论文：Supervised Sequence Labelling with Recurrent Neural Networks (详细的公式推导)

1. 理解 LSTM

(1) 前向计算

LSTM是一类可以处理长期依赖问题的特殊的RNN，由Hochreiter 和 Schmidhuber于1977年提出，目前已有多种改进，且广泛用于各种各样的问题中。LSTM主要用来处理长期依赖问题，与传统RNN相比，长时间的信息记忆能力是与生俱来的。

所有的RNN链式结构中都有不断重复的模块，用来随时间传递信息。传统的RNN使用十分简单的结构，比如 $tanh$ 层 (如下图所示)。

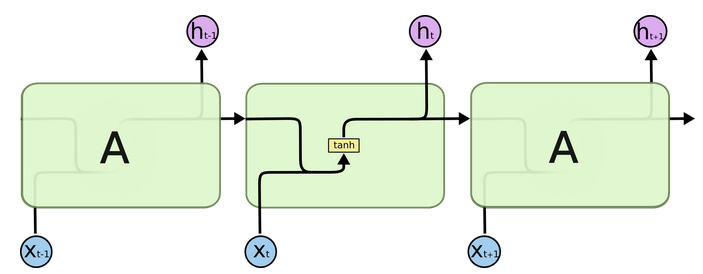
传统RNN链式结构中重复模块的单层结构( 图片来源)

LSTM链式结构中重复模块的结构更加复杂，有四个互相交互的层 (如下图所示)。

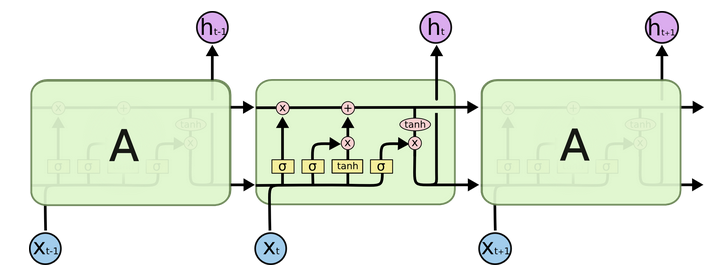
LSTM链式结构中重复模块的结构( 图片来源)

图中各种符号含义如下图所示，黄色的方框表示神经网络层，圆圈表示两个向量间逐点操作，直线箭头表示向量流向，汇聚箭头表示向量串接，分裂箭头表示向量复制流向不同的方向。

与传统RNN相比，除了拥有隐藏状态外，LSTM还增加了一个细胞状态(cell state，即下图中最上边的水平线)，记录随时间传递的信息。在传递过程中，通过当前输入、上一时刻隐藏层状态、上一时刻细胞状态以及门结构来增加或删除细胞状态中的信息。门结构用来控制增加或删除信息的程度，一般由 $sigmoid$ 函数(值域 $(0, 1)$ )和向量点乘来实现。

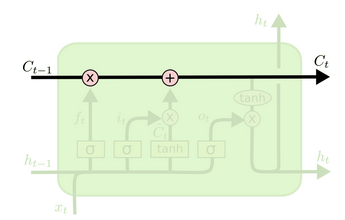
细胞状态随时间的信息传递( 图片来源)

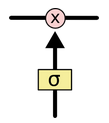
sigmoid $sigmoid$ 和点乘符号( 图片来源)

LSTM共包含3个门结构，来控制细胞状态和隐藏状态，下边分别进行介绍。

遗忘门 (output gate)

从名字易知，遗忘门决定上一时刻细胞状态 $C_{t-1}$ 中的多少信息(由 $f_t$ 控制，值域为 $(0, 1)$ ) 可以传递到当前时刻 $C_t$ 中。

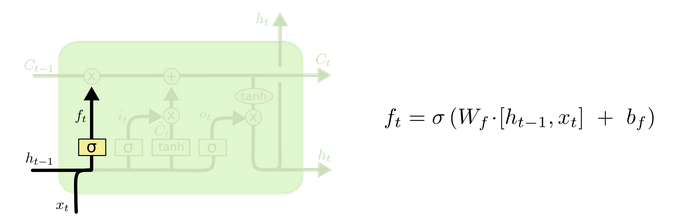
遗忘门 (forget gate) ( 图片来源)

输入门 (input gate)

顾名思义，输入门用来控制当前输入新生成的信息 $bar C_t$ 中有多少信息(由 $i_t$ 控制，值域为 $(0, 1)$ )可以加入到细胞状态 $C_t$ 中。 $tanh$ 层用来产生当前时刻新的信息， $sigmoid$ 层用来控制有多少新信息可以传递给细胞状态。

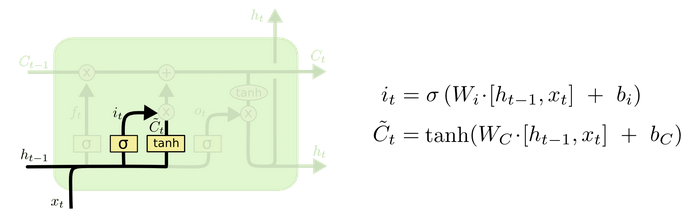
输入门 (input gate) ( 图片来源)

更新细胞状态

基于遗忘门和输入门的输出，来更新细胞状态。更新后的细胞状态有两部分构成，一，来自上一时刻旧的细胞状态信息 $C_{t-1}$ ；二，当前输入新生成的信息 $bar C_t$ 。前面提到，旧信息有遗忘门 ( $f_t$ ) 控制，值为遗忘门的输出点乘旧细胞状态 ( $f_t * C_{t-1}$ )；新信息由输入门 ( $i_t$ ) 控制，值为输入门的输出点乘新信息 $i_t * bar C_t$ 。

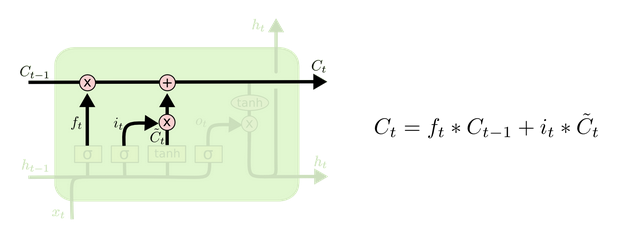
更新细胞状态 ( 图片来源)

输出门 (output gate)

最后，基于更新的细胞状态，输出隐藏状态 $h_t$ 。这里依然用 $sigmoid$ 层 (输出门， $o_t$ ) 来控制有多少细胞状态信息 ( $tanh(C_t)$ ，将细胞状态缩放至 $(-1, 1)$ ) 可以作为隐藏状态的输出 $h_t$ 。

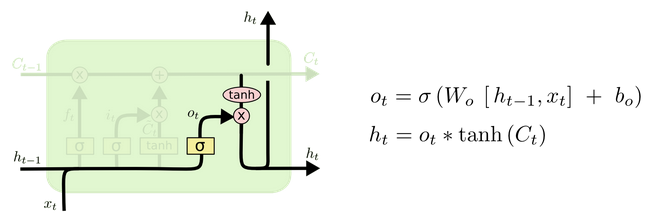
输出门 (隐藏状态的输出) ( 图片来源)

以上是LSTM的前向计算过程，下面介绍求解梯度的反向传播算法。

(2) 梯度求解：BPTT 随时间反向传播

(1) 前向计算各时刻遗忘门状态 $f_t$ 、输入门状态 $i_t$ 、当前输入新信息 $bar C_t$ 、细胞状态 $C_t$ 、输出门状态 $o_t$ 、隐藏层状态 $h_t$ 、模型输出 $y_t$ ；
(2) 反向传播计算误差 $delta$ ，即模型目标函数 $E$ 对加权输入 $net_t=(W_h*h_{t-1}+W_x*x_t+b)$ 的偏导；(注意， $delta$ 的传播沿两个方向，分别为从输出层传递至输入层，以及沿时间 $t$ 的反向传播)
(3) 求解模型目标函数 $E$ 对权重 $W_{hf}, W_{xf}, b_f; W_{hi}, W_{xi}, b_i; W_{hc}, W_{xc}, b_c; W_{ho}, W_{xo}, b_o; W_y, b_y$ 的偏导数。

$delta$ 沿时间 $t$ 的反向传播

定义 $delta_{h_t}= frac {partial E}{partial h_t}$

由于 $h_t = o_t * tanh(C_t)$
可得 $delta_{o_t}=frac {partial E}{partial o_t} = delta_{h_t} * tanh(C_t)$
$delta_{C_t}+= delta_{h_t} * o_t * (1-tanh^2(C_t))$
注意，由于 $C_t$ 记忆了所有时刻的细胞状态，故每个时间点迭代时， $delta_{C_t}$ 累加。

由于 $C_t = i_t * bar C_t + f_t * C_{t-1}$
则 $delta_{i_t} = delta_{C_t} * bar C_t$
$delta_{f_t} = delta_{C_t} * C_{t-1}$
$delta_bar {C_t} = delta_{C_t} * i_t$
$delta_ {C_{t-1}} = delta_{C_t} * f_t$

由于 $i_t = f(net_{it})=sigmoid(W_{hi}*h_{t-1}+W_{xi}*x_t+b_i)$
$f_t = f(net_{ft})=sigmoid(W_{hf}*h_{t-1}+W_{xf}*x_t+b_f)$
$bar C_t = f(net_{bar Ct})=tanh(W_{hbar C}*h_{t-1}+W_{xbar C}*x_t+b_bar C)$
$i_t = f(net_{ot})=sigmoid(W_{ho}*h_{t-1}+W_{xo}*x_t+b_o)$
故 $delta_{net_{it}} = delta_{it} * f'(net_{it})=delta_{it}*i_t*(1-i_t)$
$delta_{net_{ft}} = delta_{ft} * f'(net_{ft})=delta_{ft}*f_t*(1-f_t)$
$delta_{net_{bar Ct}} = delta_{bar Ct} * f'(net_{bar Ct})=delta_{bar Ct}*(1-bar C^2_t)$
$delta_{net_{ot}} = delta_{ot} * f'(net_{ot})=delta_{ot}*o_t*(1-o_t)$

最后，可求得各个权重矩阵的偏导数

$frac{partial E}{partial W_{hi}} += delta_{net_{it}}*h^T_{t-1}, frac{partial E}{partial W_{xi}} += delta_{net_{it}}*x^T_t, frac{partial E}{partial b_i} += delta_{net_{it}}$

$frac{partial E}{partial W_{hf}} += delta_{net_{ft}}*h^T_{t-1}, frac{partial E}{partial W_{xf}} += delta_{net_{ft}}*x^T_t, frac{partial E}{partial b_f} += delta_{net_{ft}}$

$frac{partial E}{partial W_{hbar C}} += delta_{net_{bar Ct}}*h^T_{t-1}, frac{partial E}{partial W_{xbar C}} += delta_{net_{bar Ct}}*x^T_t, frac{partial E}{partial b_bar C} += delta_{net_{bar Ct}}$

$frac{partial E}{partial W_{ho}} += delta_{net_{ot}}*h^T_{t-1}, frac{partial E}{partial W_{xo}} += delta_{net_{ot}}*x^T_t, frac{partial E}{partial b_o} += delta_{net_{ot}}$

注意以上权重参数在所有时刻共享，故每个时间点迭代时梯度累加。

某一时刻 $t, delta$ 从输出层传递至输入层

对于输出层 L ：
由于 $y_t=g(W_y*h_t+b_y)=g(net_t)$ ，则 $delta^L_{net_t}=frac{delta E}{delta y_t} *g' {(net_t)}$

可求得权重矩阵 $W_y, b_y$ 的偏导数
$frac{partial E}{partial W_Y} = delta^L_{net_t}*h^T_t$
$frac{partial E}{partial b_Y} = delta^L_{net_t}$

也可得 $delta^L_{h_t}=W_{y}^T*delta^L_{net_t}$

对于其它层 l ：
由 $net_t=(W_h*h_{t-1}+W_x*x_t+b)$
$delta^{l-1}_{h_t}=frac{delta E}{delta h_t^{l-1}}=delta^l_{h_t}*frac{delta h^l_t}{delta h_t^{l-1}}$
因为 $delta^l_{h_t}*frac{delta h^l_t}{delta h_t^{l-1}} = delta^l_{h_t}*frac{delta h^l_t}{delta o_t^l}*frac{delta o_t^l}{delta h_t^{l-1}} +delta^l_{h_t}*frac{delta h^l_t}{delta c_t^l}*frac{delta c_t^l}{delta i_t^l}frac{delta i_t^l}{delta h_t^{l-1}} +delta^l_{h_t}*frac{delta h^l_t}{delta c_t^l}*frac{delta c_t^l}{delta bar c_t^l}frac{delta bar c_t^l}{delta h_t^{l-1}} +delta^l_{h_t}*frac{delta h^l_t}{delta c_t^l}*frac{delta c_t^l}{delta f_t^l}frac{delta f_t^l}{delta h_t^{l-1}}$
故 $delta^{l-1}_{h_t}=delta^l_{h_t}*frac{delta h^l_t}{delta h_t^{l-1}} = {delta^{l}_{ot}}^T * W_{xo} * f'(net_{ot}^{l}) + {delta^{l}_{it}}^T * W_{xi} * f'(net_{it}^{l}) + {delta^{l}_{bar ct}}^T * W_{xbar c} * f'(net_{bar ct}^{l}) + {delta^{l}_{ft}}^T * W_{xf} * f'(net_{ft}^{l})$

以上是LSTM各参数的梯度求解过程，下面依照以上公式，实现一个简单的单层LSTM网络。

2. python实现LSTM

数据采用dataset available on Google’s BigQuery的前10000条评论文本，预处理描述和代码实现 tokenFile.py 同上篇博客。

单层LSTM实现代码如下：

import tokenFile import numpy as np # 输出单元激活函数 def softmax(x): x = np.array(x) max_x = np.max(x) return np.exp(x-max_x) / np.sum(np.exp(x-max_x)) def sigmoid(x): return 1.0/(1.0 + np.exp(-x)) def tanh(x): return (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x)) class myLSTM: def __init__(self, data_dim, hidden_dim=100): # data_dim: 词向量维度，即词典长度; hidden_dim: 隐单元维度 self.data_dim = data_dim self.hidden_dim = hidden_dim # 初始化权重向量 self.whi, self.wxi, self.bi = self._init_wh_wx() self.whf, self.wxf, self.bf = self._init_wh_wx() self.who, self.wxo, self.bo = self._init_wh_wx() self.wha, self.wxa, self.ba = self._init_wh_wx() self.wy, self.by = np.random.uniform(-np.sqrt(1.0/self.hidden_dim), np.sqrt(1.0/self.hidden_dim), (self.data_dim, self.hidden_dim)), np.random.uniform(-np.sqrt(1.0/self.hidden_dim), np.sqrt(1.0/self.hidden_dim), (self.data_dim, 1)) # 初始化 wh, wx, b def _init_wh_wx(self): wh = np.random.uniform(-np.sqrt(1.0/self.hidden_dim), np.sqrt(1.0/self.hidden_dim), (self.hidden_dim, self.hidden_dim)) wx = np.random.uniform(-np.sqrt(1.0/self.data_dim), np.sqrt(1.0/self.data_dim), (self.hidden_dim, self.data_dim)) b = np.random.uniform(-np.sqrt(1.0/self.data_dim), np.sqrt(1.0/self.data_dim), (self.hidden_dim, 1)) return wh, wx, b # 初始化各个状态向量 def _init_s(self, T): iss = np.array([np.zeros((self.hidden_dim, 1))] * (T + 1)) # input gate fss = np.array([np.zeros((self.hidden_dim, 1))] * (T + 1)) # forget gate oss = np.array([np.zeros((self.hidden_dim, 1))] * (T + 1)) # output gate ass = np.array([np.zeros((self.hidden_dim, 1))] * (T + 1)) # current inputstate hss = np.array([np.zeros((self.hidden_dim, 1))] * (T + 1)) # hidden state css = np.array([np.zeros((self.hidden_dim, 1))] * (T + 1)) # cell state ys = np.array([np.zeros((self.data_dim, 1))] * T) # output value return {'iss': iss, 'fss': fss, 'oss': oss, 'ass': ass, 'hss': hss, 'css': css, 'ys': ys} # 前向传播，单个x def forward(self, x): # 向量时间长度 T = len(x) # 初始化各个状态向量 stats = self._init_s(T) for t in range(T): # 前一时刻隐藏状态 ht_pre = np.array(stats['hss'][t-1]).reshape(-1, 1) # input gate stats['iss'][t] = self._cal_gate(self.whi, self.wxi, self.bi, ht_pre, x[t], sigmoid) # forget gate stats['fss'][t] = self._cal_gate(self.whf, self.wxf, self.bf, ht_pre, x[t], sigmoid) # output gate stats['oss'][t] = self._cal_gate(self.who, self.wxo, self.bo, ht_pre, x[t], sigmoid) # current inputstate stats['ass'][t] = self._cal_gate(self.wha, self.wxa, self.ba, ht_pre, x[t], tanh) # cell state, ct = ft * ct_pre + it * at stats['css'][t] = stats['fss'][t] * stats['css'][t-1] + stats['iss'][t] * stats['ass'][t] # hidden state, ht = ot * tanh(ct) stats['hss'][t] = stats['oss'][t] * tanh(stats['css'][t]) # output value, yt = softmax(self.wy.dot(ht) + self.by) stats['ys'][t] = softmax(self.wy.dot(stats['hss'][t]) + self.by) return stats # 计算各个门的输出 def _cal_gate(self, wh, wx, b, ht_pre, x, activation): return activation(wh.dot(ht_pre) + wx[:, x].reshape(-1,1) + b) # 预测输出，单个x def predict(self, x): stats = self.forward(x) pre_y = np.argmax(stats['ys'].reshape(len(x), -1), axis=1) return pre_y # 计算损失， softmax交叉熵损失函数， (x,y)为多个样本 def loss(self, x, y): cost = 0 for i in xrange(len(y)): stats = self.forward(x[i]) # 取出 y[i] 中每一时刻对应的预测值 pre_yi = stats['ys'][xrange(len(y[i])), y[i]] cost -= np.sum(np.log(pre_yi)) # 统计所有y中词的个数, 计算平均损失 N = np.sum([len(yi) for yi in y]) ave_loss = cost / N return ave_loss # 初始化偏导数 dwh, dwx, db def _init_wh_wx_grad(self): dwh = np.zeros(self.whi.shape) dwx = np.zeros(self.wxi.shape) db = np.zeros(self.bi.shape) return dwh, dwx, db # 求梯度, (x,y)为一个样本 def bptt(self, x, y): dwhi, dwxi, dbi = self._init_wh_wx_grad() dwhf, dwxf, dbf = self._init_wh_wx_grad() dwho, dwxo, dbo = self._init_wh_wx_grad() dwha, dwxa, dba = self._init_wh_wx_grad() dwy, dby = np.zeros(self.wy.shape), np.zeros(self.by.shape) # 初始化 delta_ct，因为后向传播过程中，此值需要累加 delta_ct = np.zeros((self.hidden_dim, 1)) # 前向计算 stats = self.forward(x) # 目标函数对输出 y 的偏导数 delta_o = stats['ys'] delta_o[np.arange(len(y)), y] -= 1 for t in np.arange(len(y))[::-1]: # 输出层wy, by的偏导数，由于所有时刻的输出共享输出权值矩阵，故所有时刻累加 dwy += delta_o[t].dot(stats['hss'][t].reshape(1, -1)) dby += delta_o[t] # 目标函数对隐藏状态的偏导数 delta_ht = self.wy.T.dot(delta_o[t]) # 各个门及状态单元的偏导数 delta_ot = delta_ht * tanh(stats['css'][t]) delta_ct += delta_ht * stats['oss'][t] * (1-tanh(stats['css'][t])**2) delta_it = delta_ct * stats['ass'][t] delta_ft = delta_ct * stats['css'][t-1] delta_at = delta_ct * stats['iss'][t] delta_at_net = delta_at * (1-stats['ass'][t]**2) delta_it_net = delta_it * stats['iss'][t] * (1-stats['iss'][t]) delta_ft_net = delta_ft * stats['fss'][t] * (1-stats['fss'][t]) delta_ot_net = delta_ot * stats['oss'][t] * (1-stats['oss'][t]) # 更新各权重矩阵的偏导数，由于所有时刻共享权值，故所有时刻累加 dwhf, dwxf, dbf = self._cal_grad_delta(dwhf, dwxf, dbf, delta_ft_net, stats['hss'][t-1], x[t]) dwhi, dwxi, dbi = self._cal_grad_delta(dwhi, dwxi, dbi, delta_it_net, stats['hss'][t-1], x[t]) dwha, dwxa, dba = self._cal_grad_delta(dwha, dwxa, dba, delta_at_net, stats['hss'][t-1], x[t]) dwho, dwxo, dbo = self._cal_grad_delta(dwho, dwxo, dbo, delta_ot_net, stats['hss'][t-1], x[t]) return [dwhf, dwxf, dbf, dwhi, dwxi, dbi, dwha, dwxa, dba, dwho, dwxo, dbo, dwy, dby] # 更新各权重矩阵的偏导数 def _cal_grad_delta(self, dwh, dwx, db, delta_net, ht_pre, x): dwh += delta_net * ht_pre dwx += delta_net * x db += delta_net return dwh, dwx, db # 计算梯度, (x,y)为一个样本 def sgd_step(self, x, y, learning_rate): dwhf, dwxf, dbf, dwhi, dwxi, dbi, dwha, dwxa, dba, dwho, dwxo, dbo, dwy, dby = self.bptt(x, y) # 更新权重矩阵 self.whf, self.wxf, self.bf = self._update_wh_wx(learning_rate, self.whf, self.wxf, self.bf, dwhf, dwxf, dbf) self.whi, self.wxi, self.bi = self._update_wh_wx(learning_rate, self.whi, self.wxi, self.bi, dwhi, dwxi, dbi) self.wha, self.wxa, self.ba = self._update_wh_wx(learning_rate, self.wha, self.wxa, self.ba, dwha, dwxa, dba) self.who, self.wxo, self.bo = self._update_wh_wx(learning_rate, self.who, self.wxo, self.bo, dwho, dwxo, dbo) self.wy, self.by = self.wy - learning_rate * dwy, self.by - learning_rate * dby # 更新权重矩阵 def _update_wh_wx(self, learning_rate, wh, wx, b, dwh, dwx, db): wh -= learning_rate * dwh wx -= learning_rate * dwx b -= learning_rate * db return wh, wx, b # 训练 LSTM def train(self, X_train, y_train, learning_rate=0.005, n_epoch=5): losses = [] num_examples = 0 for epoch in xrange(n_epoch): for i in xrange(len(y_train)): self.sgd_step(X_train[i], y_train[i], learning_rate) num_examples += 1 loss = self.loss(X_train, y_train) losses.append(loss) print 'epoch {0}: loss = {1}'.format(epoch+1, loss) if len(losses) > 1 and losses[-1] > losses[-2]: learning_rate *= 0.5 print 'decrease learning_rate to', learning_rate

代码执行示例：

# 获取数据 file_path = r'/home/display/pypys/practices/rnn/results-20170508-103637.csv' dict_size = 8000 myTokenFile = tokenFile.tokenFile2vector(file_path, dict_size) X_train, y_train, dict_words, index_of_words = myTokenFile.get_vector() # 训练LSTM lstm = myLSTM(dict_size, hidden_dim=100) lstm.train(X_train[:200], y_train[:200], learning_rate=0.005, n_epoch=3)

执行结果如下：

Get 24700 sentences. Get 30384 words. epoch 1: loss = 6.30601281865 epoch 2: loss = 6.05770746549 epoch 3: loss = 5.92739836912

3. 总结

本文对LSTM的结构和训练过程做了一个简要介绍，并实现了一个toy model，目的在于加深对LSTM工作原理的理解。