1. 首页
  2. 文章中心
  3. 笔记

小波变换（matlab）-常见脚本函数前言一、小波变换的介绍和理解二、常用函数三、wavelet toolbox的应用

146 阅读 0 评论
我是靠谱客的博主 狂野季节，这篇文章主要介绍小波变换（matlab）-常见脚本函数前言一、小波变换的介绍和理解二、常用函数三、wavelet toolbox的应用，现在分享给大家，希望可以做个参考。

小波变换

  • 前言
  • 一、小波变换的介绍和理解
  • 二、常用函数
    • 1.wden
    • 2.dwt和idwt
    • 3.wavedec和wrcoef
    • 4.upwlev
    • 5.wpdec和wprec
  • 三、wavelet toolbox的应用

前言

我们可以通过常见的函数和toolbox两个办法来制定我们需要的小波变换，因为它与傅里叶不同点在于小波变换不是唯一确定的，例如不同的尺度下做的小波变换会不一样。小波变换的函数有很多，本文给了最常见的几种。在toolbox使用中，也会对比函数，整理各个参数的涵义。下图是常见的小波基函数参数表示和名称，其中的N是可以调节的整数。
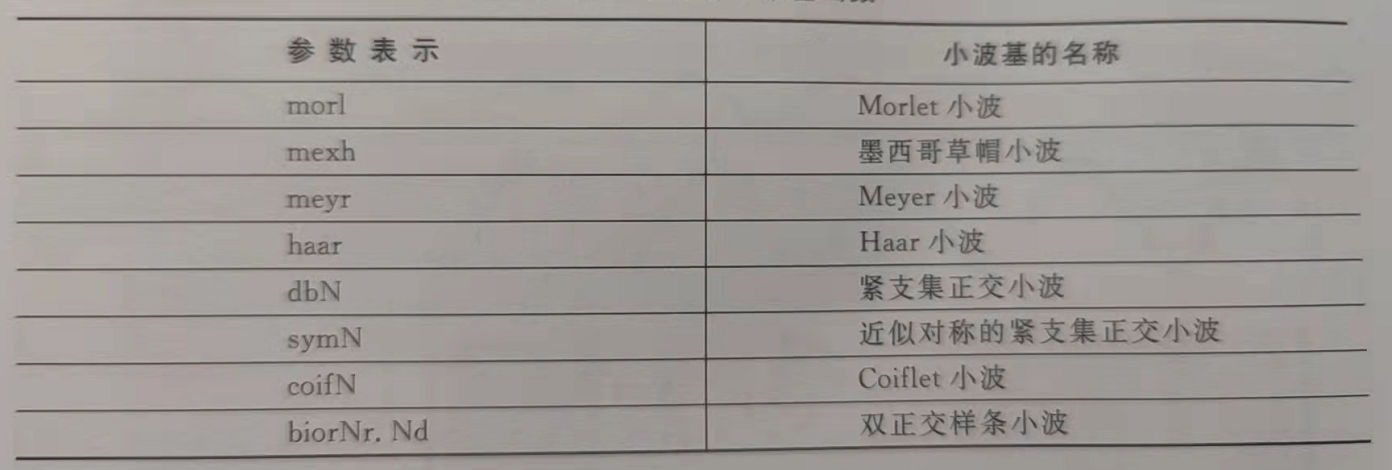
在这里插入图片描述

一、小波变换的介绍和理解

小波变换是一种时域变换，是傅里叶分析的发展和延拓。相对于傅里叶变换，它除了是不唯一确定以外，它还很适用于非平稳信号。因为对于傅里叶变换而言，不同的非平稳信号的时域对应的频域都是一样的，这就说明无法从频域角度重构时域信号。再者就是二者的基不一样，小波基是不一样的，可以理解成短时傅里叶变换的窗是会自适应变换的。

二、常用函数

1.wden

wden函数是一种用小波进行一维信号的消噪或压缩的函数。
实例函数和结果如下所示，其中为了防止随机数的种子被固定，需要使其rng重新配置。

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
%%% wden函数：用小波进行一维信号的消噪或压缩
%%%  XD = wden(X,TPTR,SORH,SCAL,N,'wname')
%1.输入参数SORH=s，软阈值;Sorh=h，硬阈值；
%2.输入参数scal规定了阈值处理随噪声水平的变化：
%SCAL=one，不随噪声水平变化。
%SCAL=mln，根据每一层小波分解的噪声水平估计进行调整。
%SCAL=sln，根据第一层小波分解的噪声水平估计进行调整。
%3.wname是小波函数类型的选用
clc;close all;clear all;
rng('default');                            %随机种子重新设置
seed=2055415866;
snr=3;                                     %设置信噪比;
[xref,x]=wnoise(1,11,snr,seed);            %产生非平稳含噪信号;
N=4;
SCAL='sln';
SORH='s';
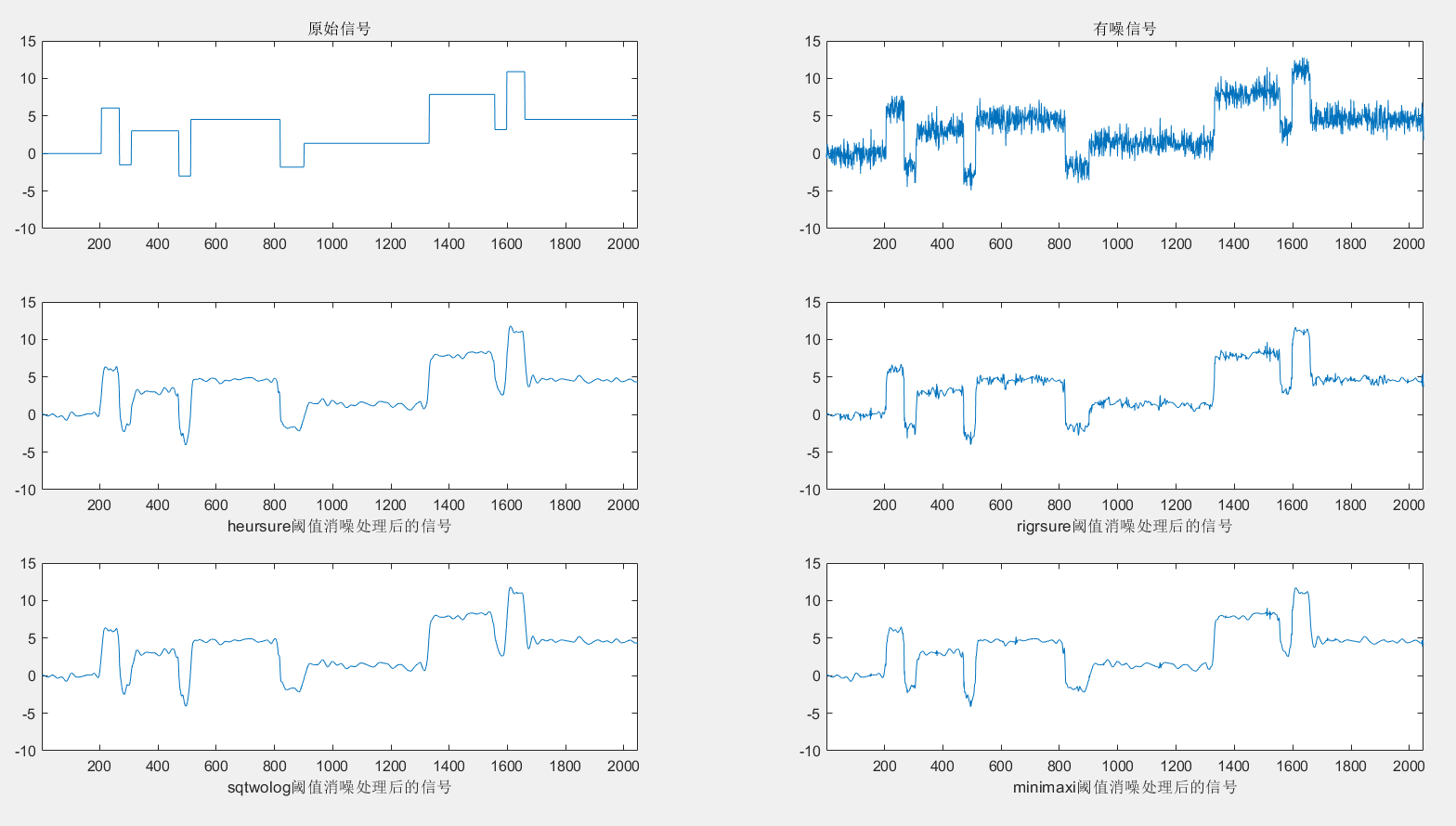
xdH=wden(x,'heursure',SORH,SCAL,N,'sym6');  %heursure阈值信号处理；
xdR=wden(x,'rigrsure',SORH,SCAL,N,'sym6');  %rigrsure阈值信号处理；
xdS=wden(x,'sqtwolog',SORH,SCAL,N,'sym6');  %sqtwolog阈值信号处理；
xdM=wden(x,'minimaxi',SORH,SCAL,N,'sym6');  %minimaxi阈值信号处理；
subplot(3,2,1);
plot(xref);title('原始信号');
axis([1,2048,-10,15]);
subplot(3,2,2);
plot(x);title('含噪信号');
axis([1,2048,-10,15]);
subplot(3,2,3);
plot(xdH);xlabel('heursure阈值消噪处理后的信号');
axis([1,2048,-10,15]);
subplot(3,2,4);
plot(xdR);xlabel('rigrsure阈值消噪处理后的信号');
axis([1,2048,-10,15]);
subplot(3,2,5);
plot(xdS);xlabel('sqtwolog阈值消噪处理后的信号');
axis([1,2048,-10,15]);
subplot(3,2,6);
plot(xdM);xlabel('minimaxi阈值消噪处理后的信号');
axis([1,2048,-10,15]);

在这里插入图片描述

2.dwt和idwt

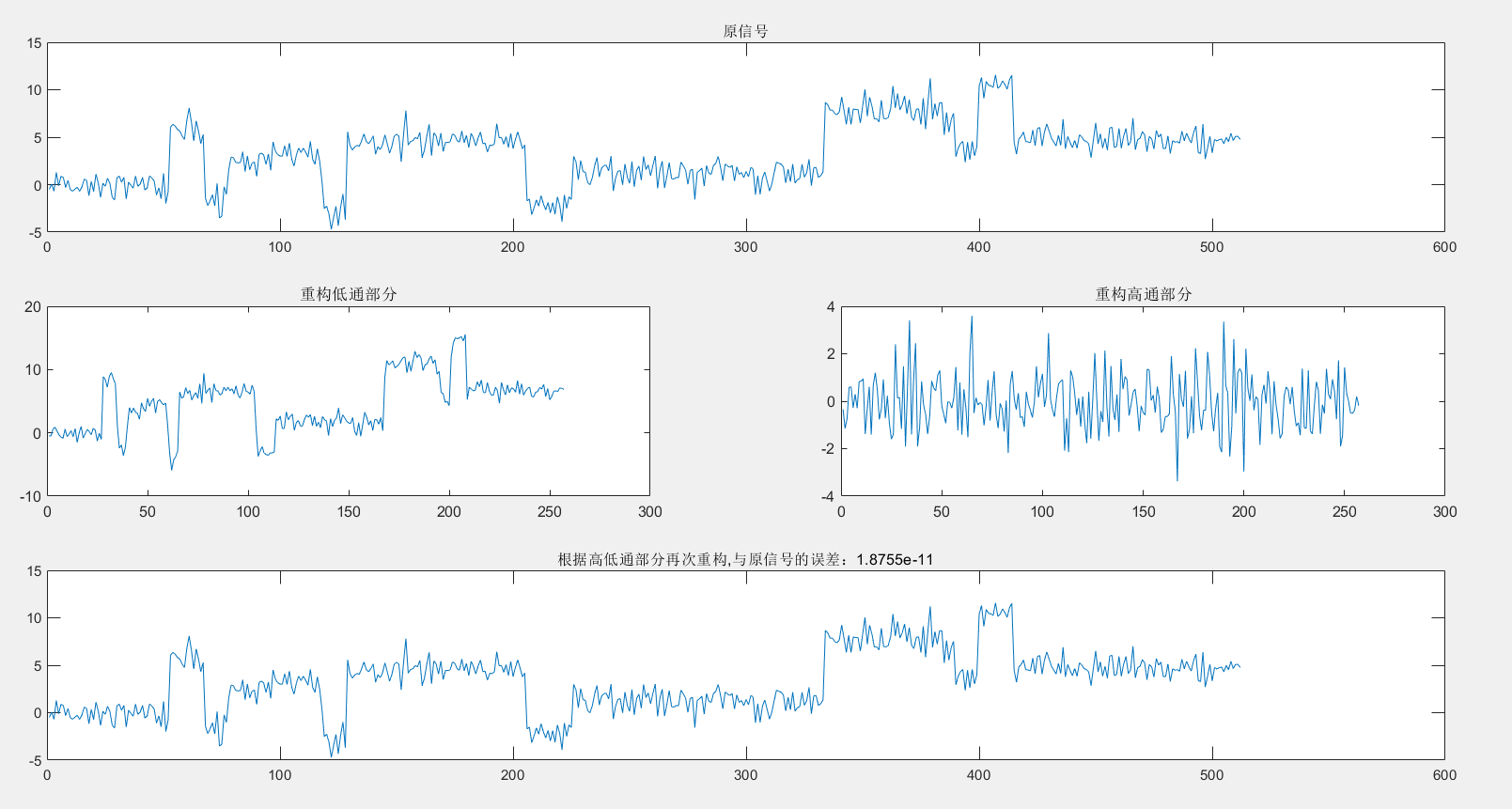
dwt和idwt是一维离散小波（反）变换。其实例和结果如下。其中，小波变换的参数ca1值得是”大概信号”，也就相对于低频，ad1值得是“细节信号”，也就相对于高频。

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
%%% dwt：单尺度一维离散小波变换
clear all;clc;close all;
% x=4+kron(ones(1,8),[1 -1])+((1:16).^2)/24+0.3*randn(1,16);
seed=2055415866;
snr=3;                                     %设置信噪比;
[xref,x]=wnoise(1,9,snr,seed);            %产生非平稳含噪信号;
[ca1,ad1]=dwt(x,'db2');
s=idwt(ca1,ad1,'db2');
err=norm(x-s);
figure;
subplot(3,2,[1 2]);
plot(x);title('原信号');
subplot(323);
plot(ca1);title('重构低通部分');
subplot(324);
plot(ad1);title('重构高通部分');
subplot(3,2,[5 6]);
plot(s);title(['根据高低通部分再次重构,与原信号的误差：',num2str(err)]);

在这里插入图片描述

3.wavedec和wrcoef

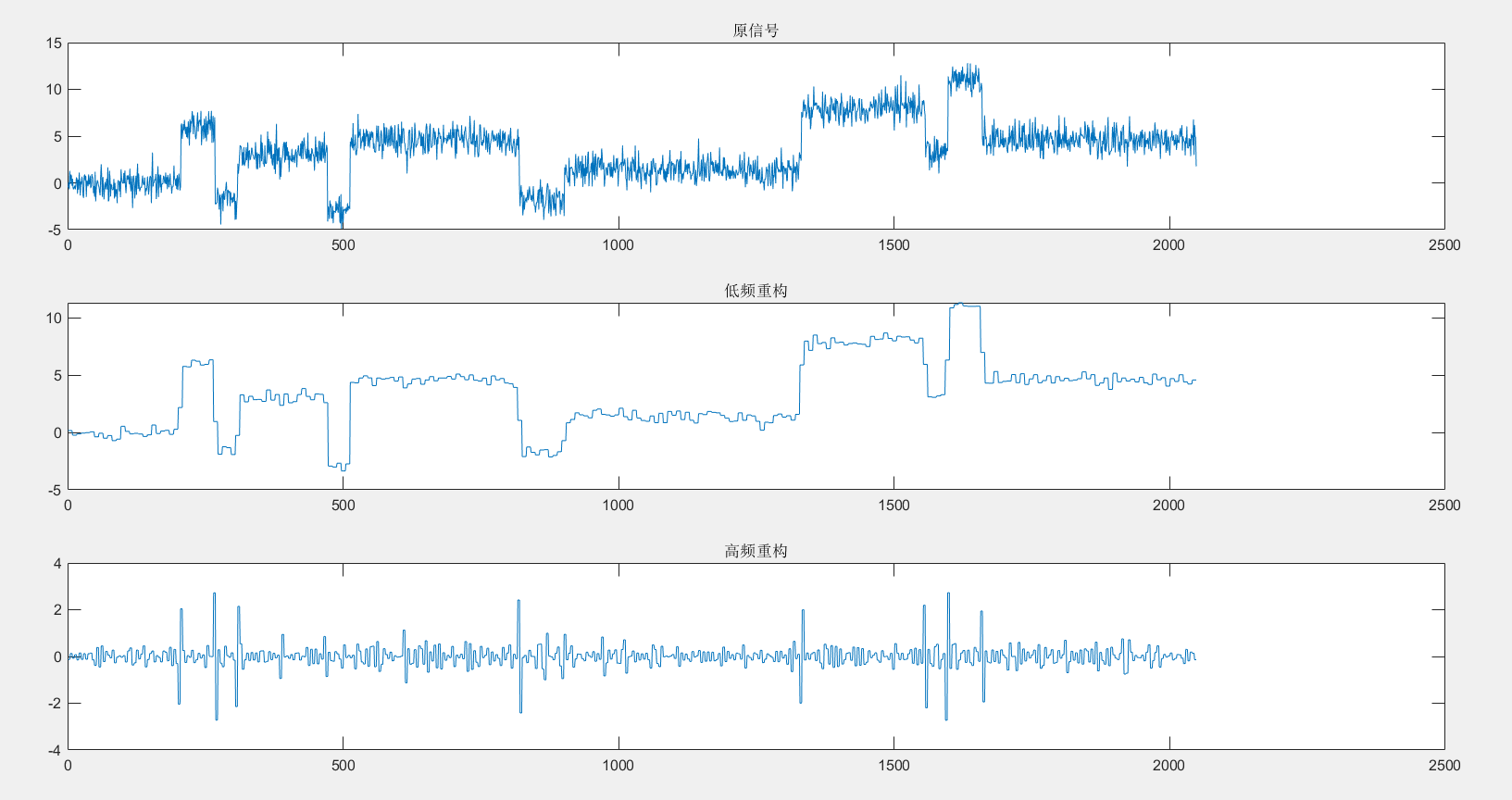
wavedec函数和wrcoef函数也比较常用，wavedec函数是用于小波变换的多层次重构。wrcoef函数是用于对小波系数进行重构。

复制代码
1
2
3
4
5
6
7
%%% wavedec函数：多层次单尺度一维小波分解
%%% [C,L]=wavedec(x,N,wname);
%%% [C,L]=wavedec(x,N,Lo_R,Hi_R);
%%% wrcoef函数：对一维小波系数进行单支重构
%%% s=wrcoef('type',C,L,'wname',N)   含N表示对N进行重构
%%% s=wrcoef('type',C,L,Lo_R,Hi_R,N)

它的实例和结果如下。

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
%%% wavedec函数：多层次单尺度一维小波分解
%%% [C,L]=wavedec(x,N,wname);
%%% [C,L]=wavedec(x,N,Lo_R,Hi_R);
clear all;clc;close all;
% rng('default');                          %随机种子重新设置
seed=2055415866;
snr=3;                                     %设置信噪比;
[xref,x]=wnoise(1,11,snr,seed);            %产生非平稳含噪信号;
wname='db1';
N=3;   %进行3尺度小波分解
%%% wrcoef函数：对一维小波系数进行单支重构
%%% s=wrcoef('type',C,L,'wname',N)   含N表示对N进行重构
%%% s=wrcoef('type',C,L,Lo_R,Hi_R,N)
type='a';   %a是大概approximation（低频）；d是细节detail（高频）                 %
[C,L]=wavedec(x,N,wname);
sa=wrcoef(type,C,L,wname,N);               %N不加，默认为3
sd=wrcoef('d',C,L,wname);
figure;
subplot(311);
plot(x);   title('原信号');
subplot(312);
plot(sa);  title('低频重构');
subplot(313);
plot(sd);  title('高频重构');

在这里插入图片描述

4.upwlev

其实upwlev就是将尺度往上返回了一级，其实与手动将wavedec中的N系数减一是等效的。
其实例和结果如下。其中为了体现这一点，程序也验证了这一点。除此之外，也给出了对不同尺度上的低频（高频）的信号重构进行了对比。

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
clear all;clc;close all;
% load sumsin;
% s=sumsin(1:500);
rng('default');                            %随机种子重新设置
seed=2055415866;
snr=3;                                     %设置信噪比;
[xref,x]=wnoise(1,11,snr,seed);            %产生非平稳含噪信号;
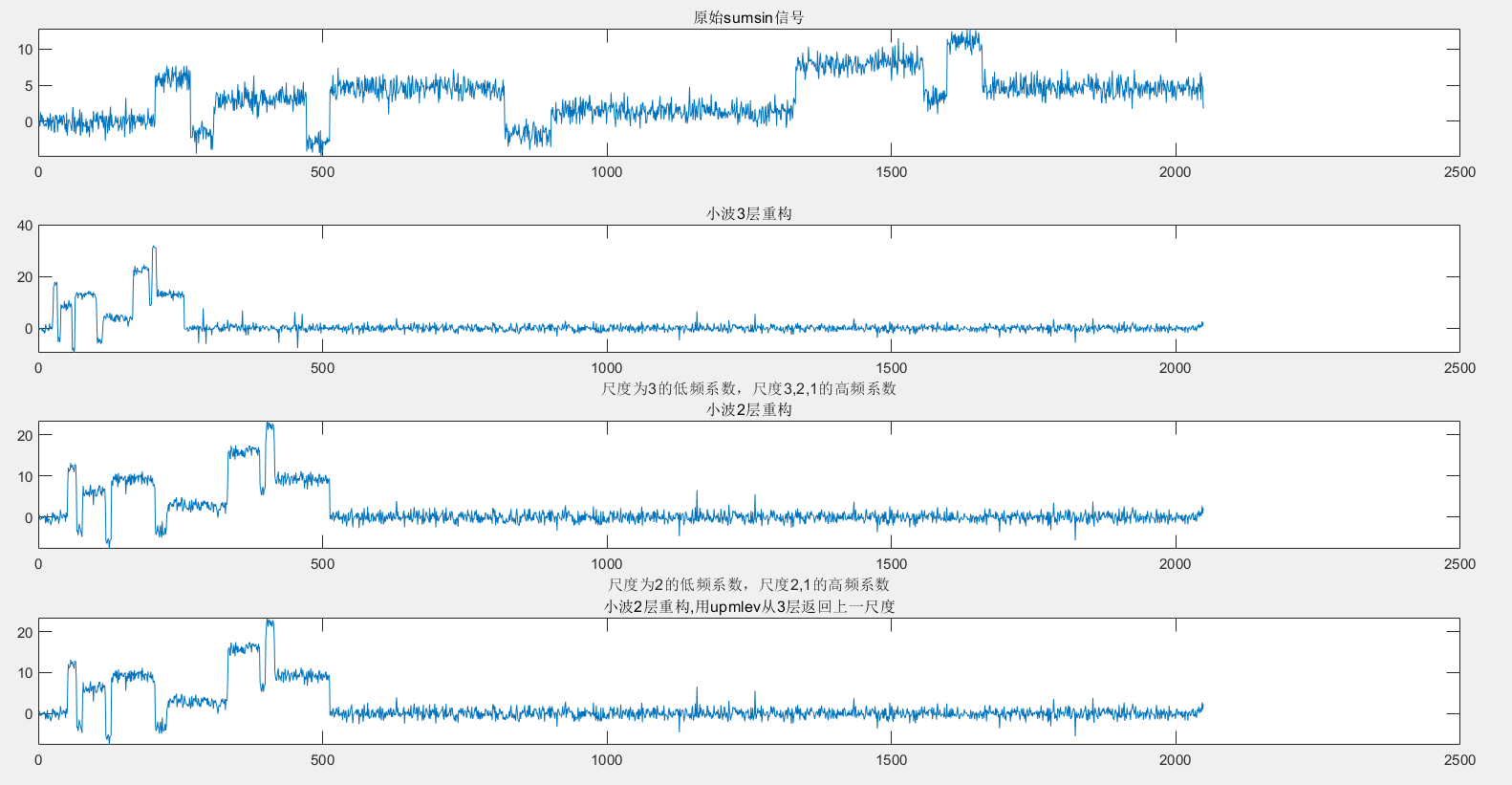
subplot(411);plot(x);
title('原始sumsin信号');
[c,l]=wavedec(x,3,'db1');
subplot(412);plot(c);
title('小波3层重构');
xlabel('尺度为3的低频系数，尺度3,2,1的高频系数');
[c1,l1]=wavedec(x,2,'db1');
subplot(413);plot(c1);
title('小波2层重构');
xlabel('尺度为2的低频系数，尺度2,1的高频系数');
[nc,nl]=upwlev(c,l,'db1');
subplot(414);plot(nc);
title('小波2层重构,用upmlev从3层返回上一尺度');
figure;
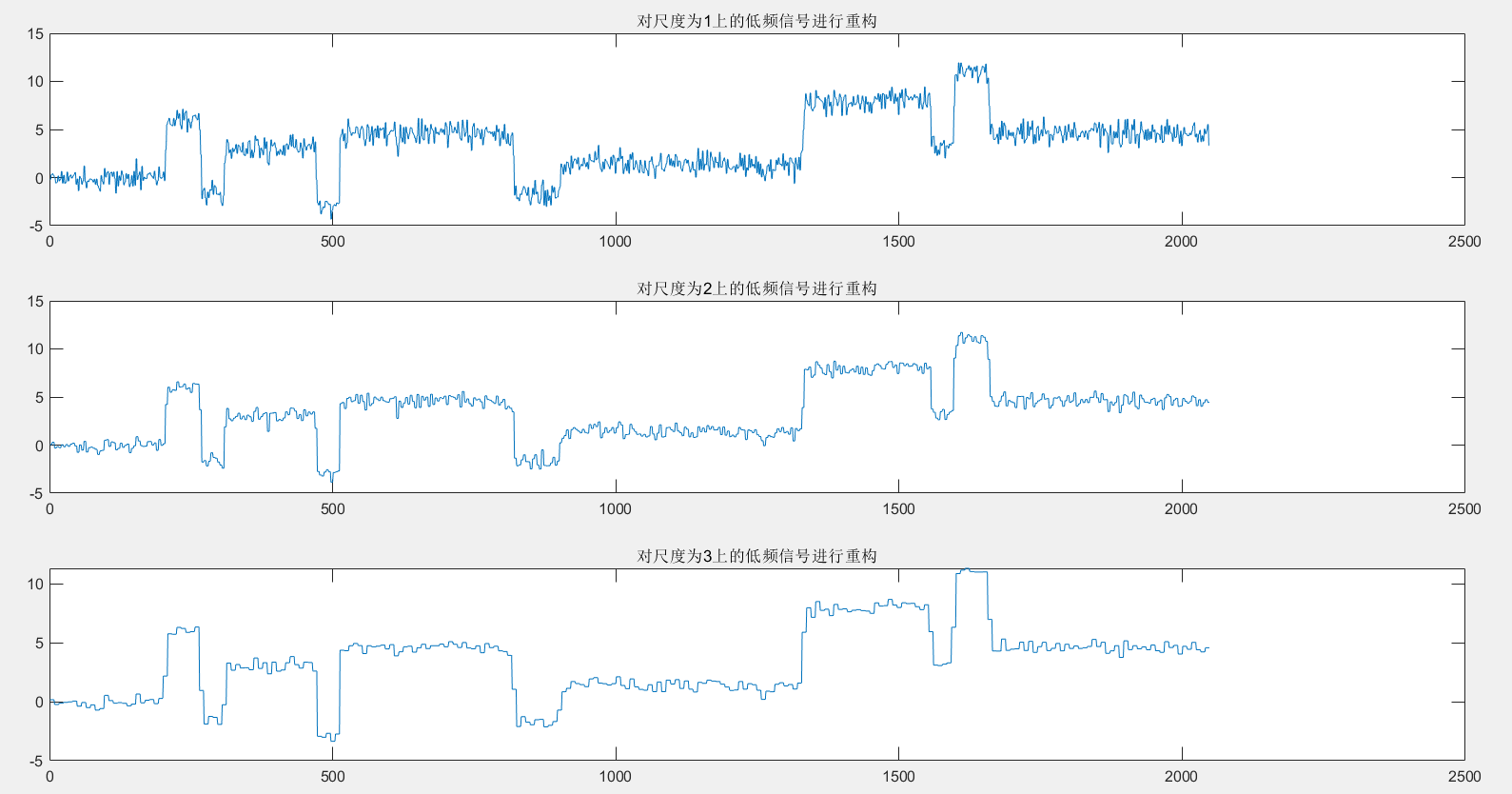
for i=1:3
    a(i,:)=wrcoef('a',c,l,'db1',i);
    subplot(3,1,i);plot(a(i,:));title(['对尺度为',num2str(i),'上的低频信号进行重构']);
end
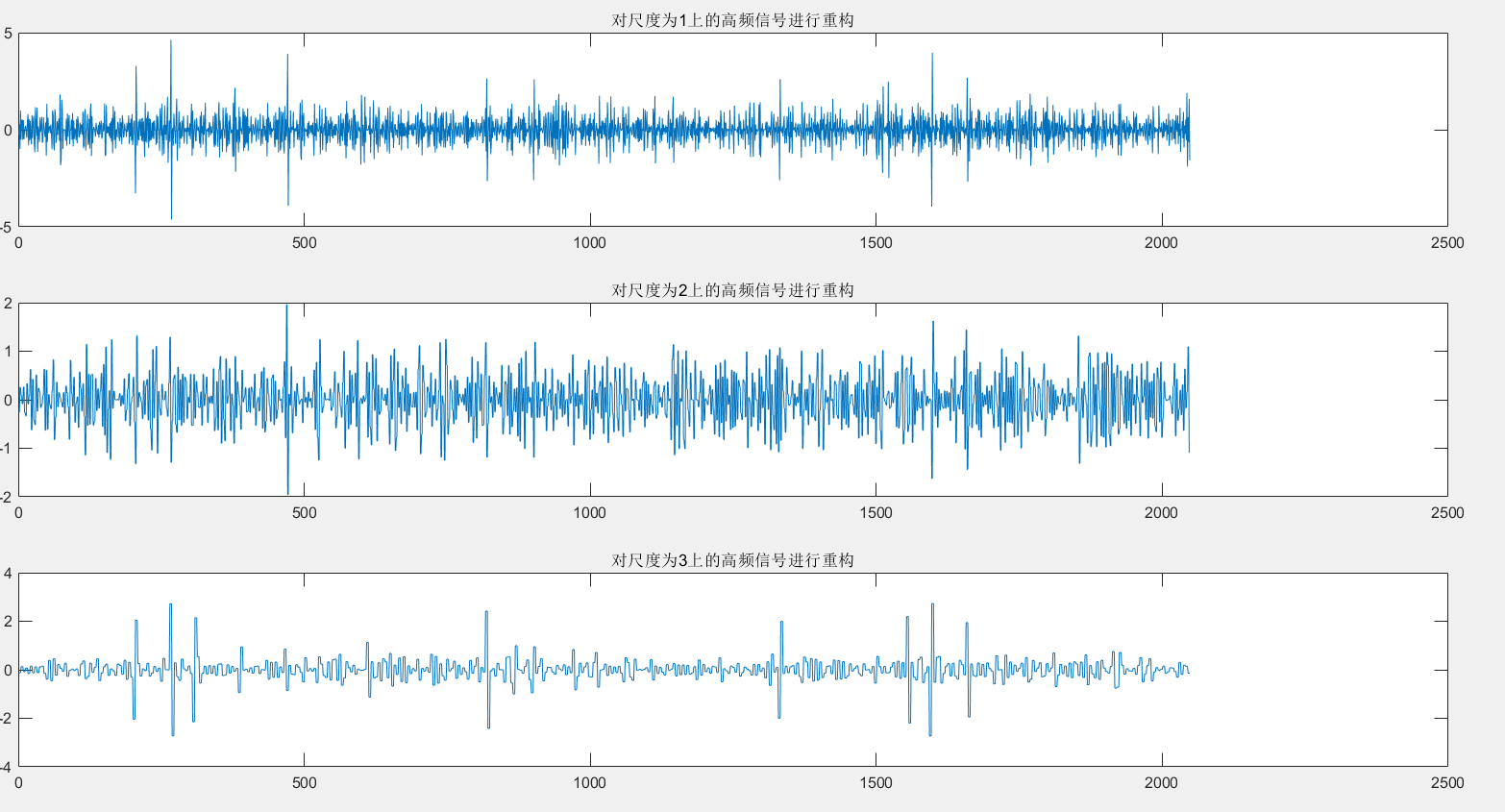
figure;
for i=1:3
    b(i,:)=wrcoef('d',c,l,'db1',i);
    subplot(3,1,i);plot(b(i,:));title(['对尺度为',num2str(i),'上的高频信号进行重构']);
end

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

5.wpdec和wprec

wpdec和wprec这两个函数是对一维小波包进行分解和重构。
wprcoef函数是对小波包分解系数的重构，这里没有举例，应用到了包结点。

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
clear all;clc;close all;
%%% wprec和wpdec函数
% load sumsin;
% x=sumsin(1:500);
rng('default');                            %随机种子重新设置
seed=2055415866;
snr=3;                                     %设置信噪比;
[xref,x]=wnoise(1,11,snr,seed);            %产生非平稳含噪信号;
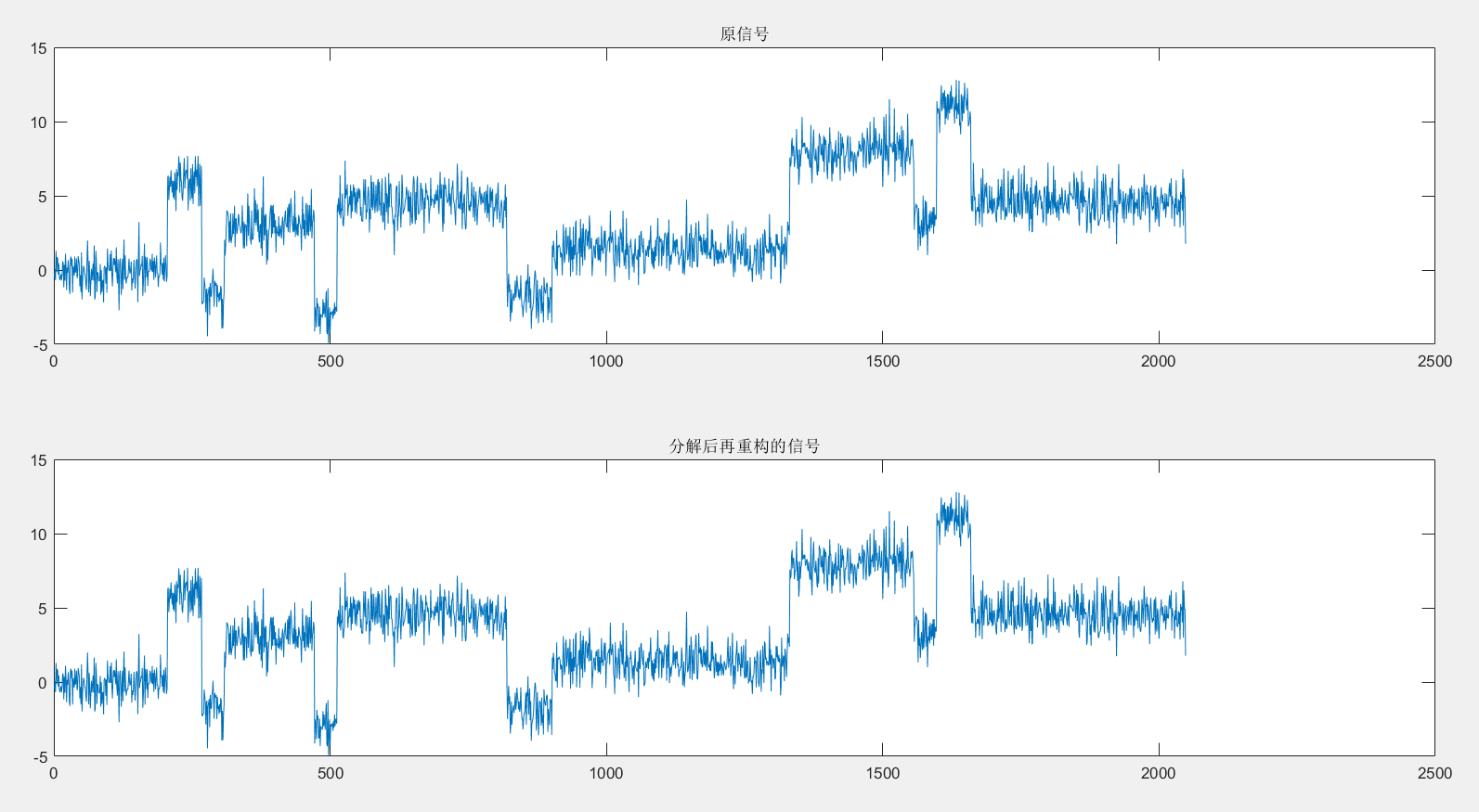
wpt=wpdec(x,3,'db2');
rex=wprec(wpt);
subplot(211);plot(x);title('原信号');
subplot(212);plot(rex);title('分解后再重构的信号');

在这里插入图片描述

三、wavelet toolbox的应用

下节介绍

最后

以上就是狂野季节最近收集整理的关于小波变换（matlab）-常见脚本函数前言一、小波变换的介绍和理解二、常用函数三、wavelet toolbox的应用的全部内容，更多相关小波变换（matlab）-常见脚本函数前言一、小波变换的介绍和理解二、常用函数三、wavelet内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(97)

相关文章

Matlab 仿真——单自由度倒立摆（2）系统分析
Matlab 仿真——单自由度倒立摆（2）系统分析
matlab中计数函数,科学网—matlab最基本的统计函数 - 管俊彪的博文
matlab中计数函数,科学网—matlab最基本的统计函数 - 管俊彪的博文
【工具】字节码指令表
【工具】字节码指令表
matlab文件路径操作 mfilename
matlab文件路径操作 mfilename
小波变换（matlab）-常见脚本函数前言一、小波变换的介绍和理解二、常用函数三、wavelet toolbox的应用
小波变换（matlab）-常见脚本函数前言一、小波变换的介绍和理解二、常用函数三、wavelet toolbox的应用
matlab附录
matlab附录
常用的matlab函数命令
常用的matlab函数命令
matlab怎么调用主函数,Matlab中一个函数调用另外一个函数的操作步骤
matlab怎么调用主函数,Matlab中一个函数调用另外一个函数的操作步骤

评论列表共有 0 条评论

立即
投稿
返回
顶部