初识MIMO（二）：MIMO的信道容量

一. SVD简介

• SVD可以将一个矩阵分解为$U\Sigma V^H$的形式，U是大小为$N_{RX}$的方阵，V是大小为$N_{TX}$的方阵，$\Sigma$的大小是$N_{RX}\ast N_{TX}$，对角矩阵的值为矩阵的奇异值，奇异值的个数是行列的较小值。
• 在RX和TX不相等的情况下，可以化简H
• $H{H}^H$是一个自共轭对称矩阵，9.4表示的是对称矩阵的特征值分解的形式
• 非对称矩阵也是可以特征值分解的！

SVD我没有系统 学习过，这里就不班门弄斧了

二.确定性MIMO的信道容量

1.已知CSI时

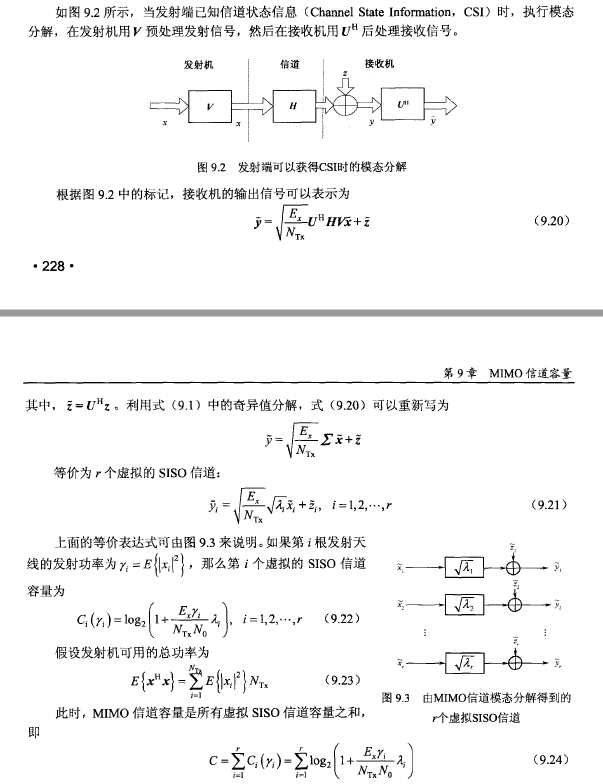
• 信道容量是互信息定义的，总的来说，记住9.19就可以了
• 发射机和接收机增加V和H可以巧妙地SVD，如何得到的呢？CSI估计出了H
• SVD分解后MIMO变为独立的SISO的和了，挨个计算
• 最后是在发射功率和限制的情况下，去求最大的容量
• 而解法是注水法

2.发射端未知CSI

• 发射端未知时，首先假设发射天线功率平均分配得到9.31
• 再当所有信道奇异值相同时H最大，这是均值不等式

3.SIMO和MISO

• SIMO不多提，使用的也不多，结论就是接受数目越多容量越大，CSI也不能起到作用
• MISO是要大书特书的
  • 如果不知道CSI，我们就平均发送，得到的结果是和SISO一样的，但可靠性提高了，这就是分集
  • 如果知道CSI，我们可以对x预编码一个$\frac{h^H}{||h||}$这样接受信号的功率就提高了，而总增益$\sum (\frac{h^H}{||h||})$^2是不变的！这就是波束赋形！

三. 随机MIMO信道容量

• 这里引入了一些随机过程，所谓遍历行说的是他在时空上任何位置都是相同的，然后我们可以计算容量的期望作为平均期望
• 中断容量是和CDF对应的 ，可以从书中图看到

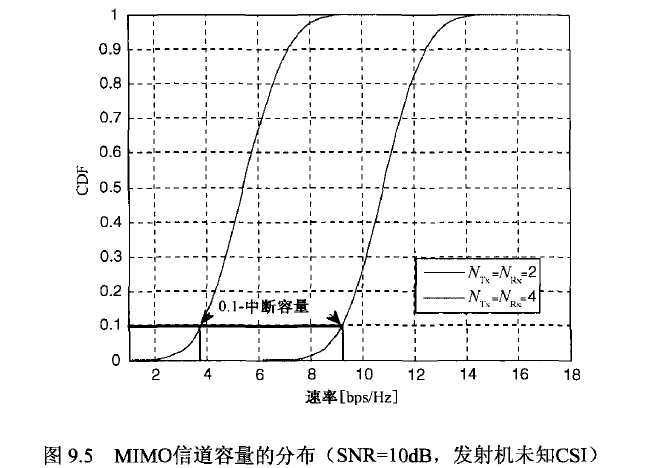
4. 信道容量和相关系数的简化运算

这一块对于信道的定义和后面相关系数为负的证明是很精彩的

四.MIMO信道仿真

1. 信道容量的CDF

代码展示

%-----------------------MIMO信道的CDF----------------%
%-----------------------author:lzx-------------------------%
%-----------------------date:09点34分-----------------%
% Ergodic_Capacity_CDF.m
%% 设置参数
clear;
figure
SNR_dB = 10; % 设定信噪比
SNR = 10.^(SNR_dB / 10.); % 转化信噪比
N_iter = 50000; % 迭代次数
grps = ['b:'; 'b-']; % 画图
C = zeros(1, N_iter); % 信道容量初始化
N_hist = 50; % 直方图分成多少份
CDFs = zeros(2, N_hist); % CDF 初始化
Rates = zeros(1, N_hist); %传输速率,这实际上就是容量
%% 主函数
for Icase = 1:2
% 测试2*2和4*4两种情况
if Icase == 1
nT = 2;
nR = 2; % 2x2
else
nT = 4;
nR = 4; % 4x4
end
rank = min(nT, nR); % 秩
I = eye(rank);
for iter = 1:N_iter
H = sqrt(1/2) * (randn(nR, nT) + 1j * randn(nR, nT)); % 先假设信道是完全独立的，信道就可以建模为瑞利信道
C(iter) = log2(real(det(I + SNR / nT * (H' * H))));% 信道容量计算，H'*H本身计算结果就是实数，这里只是做一个类型转换
% C(iter) = log2(det(I + SNR / nT * (H' * H)));% 信道容量计算
end
figure(1);
hist = histogram(C, N_hist);
PDF = hist.Values / N_iter;
for i = 1:N_hist
Rates(i) = (hist.BinEdges(i) + hist.BinEdges(i + 1)) / 2;
end
for i = 1:N_hist
CDFs(Icase, i) = sum(PDF([1:i]));
end
figure(2);
plot(Rates, CDFs(Icase, :), grps(Icase, :));
hold on
end
%% 画图
xlabel('Rate[bps/Hz]');
ylabel('CDF');
axis([1 18 0 1]);
grid on;
set(gca, 'fontsize', 10);
legend('{it N_T}={it N_R}=2', '{it N_T}={it N_R}=4');

一些值得讨论的点

1. 为什么信道被表示成了H = sqrt(1/2) * (randn(nR, nT) + 1j * randn(nR, nT));？

这是一个经典的瑞利信道，为什么可以表示为瑞利信道？

这里可以回看书中第三章的内容，如果H是一个单纯的瑞利信道，这表明信道是完全独立的，每一个MS之间都没有关系，每一个BS之间也没有关系。

而陈老湿的这篇博客中也给出了解释，为什么无关的MIMO信道是瑞利信道https://zhuanlan.zhihu.com/p/372500189

2. 为什么MIMO的公式是信道直接和信号相乘而不是卷积？

当寻找这个问题的时候，居然看见了上面提到的博客，陈老湿和我有一模一样的疑问！不过他能够自己搜索资料回答我还是很佩服的，比我更厉害！这种能找到有相同思考的人实在是太惊喜了

陈老湿给出的结论是MIMO是按照平坦信道建模的，因此可以直接相乘，目前我只能这样理解，不过第三章的IST-IMETRA模型明明是考虑了TDL的，不理解。。。

3. C(iter) = log2(real(det(I + SNR / nT * (H’ * H))));，这里为什么要取实部？

这是输出一下结果就知道，结果就是个实数，因为是埃尔米特积的结果嘛，这里只是做一个类型转换，不然后面是无法用histogram进行统计的

2. SNR对信道容量的影响

代码展示

%------------------MIMO信道容量和信噪比的影响---------------%
%-----------------------author:lzx-------------------------%
%-----------------------date:21点43分-----------------%
% Ergodic_Capacity_vs_SNR.m
%% 参数设置
clear;
SNRs_dB=[0:5:20];
% 信噪比
SNRs=10.^(SNRs_dB/10.);
N_SNR = length(SNRs);
N_iter=1000;
% 迭代次数
NTRs = [1 1; 1 2; 2 1; 4 2; 4 4];
% 天线个数，每一行是一种情况
Ncase = size(NTRs, 1);
% 测试不同情况的个数
C = zeros(Ncase, N_SNR);
%% 主函数
for iicase = 1:Ncase
% 初始化天线个数
NT = NTRs(iicase, 1);
NR = NTRs(iicase, 2);
rank = min(NT, NR);
I = eye(rank);
for iiiter = 1:N_iter
H = sqrt(0.5)*(randn(NR,NT)+1j*randn(NR,NT));
% 为了和单位矩阵保持一致
if NR>=NT
HH = H'*H;
else
HH = H*H';
end
for iiSNR = 1:N_SNR
C(iicase,iiSNR) = C(iicase,iiSNR)+log2(real(det(I+SNRs(iiSNR)/NT*HH)));
end
end
end
C = C/N_iter;
plot(SNRs_dB,C(1,:),'b-o', SNRs_dB,C(2,:),'b-<', SNRs_dB,C(3,:),'b-s',SNRs_dB,C(4,:),'b->', SNRs_dB,C(5,:),'b-^');
xlabel('SNR[dB]');
ylabel('bps/Hz');
set(gca,'fontsize',10);
grid on
s1='{it N_T}=1,{it N_R}=1';
s2='{it N_T}=1,{it N_R}=2';
s3='{it N_T}=2,{it N_R}=1';
s4='{it N_T}=2,{it N_R}=2';
s5='{it N_T}=4,{it N_R}=4';
legend(s1,s2,s3,s4,s5)

一些思考

1. 为什么要有代码

if NR>=NT
HH = H'*H;
else
HH = H*H';
end

要和单位矩阵保持一致啊！这样才是满秩的

2. 看看信噪比带来的影响吧

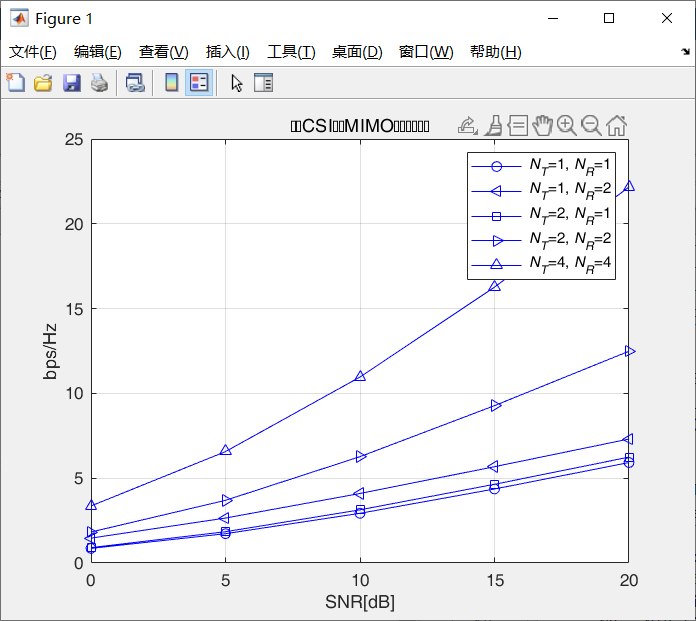
首先SNR越大容量越大，这从公式里很容易看出来，其次

对比1*1和2*1，可以看到，容量几乎一样，这符合前文所述

MISO信道容量几乎不变，但分集带来了可靠性

看1*2的SIMO信道，他是SISO的NT倍

看一下4*4的MIMO，他是未知CSI的情况，它相当于rank个SISO信道

3. 频率注水法

代码展示

%------------------已知和未知CSI的信道容量对比---------------%
%-----------------------author:lzx-------------------------%
%-----------------------date:22点07分-----------------%
%OL_CL_Comparison.m
%% 设置参数
clear;clc;
SNRs_dB=[0:5:20];
% 信噪比
SNRs=10.^(SNRs_dB/10.);
N_SNR = length(SNRs);
% 信噪比长度
N_iter=1000;
% 迭代次数
NT=4;
% 4*4矩阵
NR=4;
rank=min(NT,NR);
% MIMO的秩
I = eye(rank);
% 单位矩阵
rho=0.2;
% 相关系数
Rtx=[1
rho
rho^2
rho^3;
% 发射相关矩阵
rho
1
rho
rho^2;
rho^2
rho
1
rho;
rho^3
rho^2
rho
1];
Rrx=[1
rho
rho^2
rho^3;
% 接受相关矩阵
rho
1
rho
rho^2;
rho^2
rho
1
rho;
rho^3
rho^2
rho
1];
C_OL=zeros(1,length(SNRs_dB));
C_CL=zeros(1,length(SNRs_dB));
%% 主函数
for iiter=1:N_iter
Hiid = sqrt(1/2)*(randn(NT,NR) + 1j*randn(NT,NR));
% 生成一个独立同分布H
H = Rrx^(1/2)*Hiid*Rtx^(1/2);
% 窄带信道
sigma = svd(H'*H);
for i=1:N_SNR
%random channel generation
C_OL(i) = C_OL(i) + log2(det(I+SNRs(i)*(H'*H)/NT));
% Gamma = Water_Pouring(sigma,SNRs(i),NT);
Gamma = WaterFilling(H, rank, SNRs(i), NT);
C_CL(i) = C_CL(i)+log2(det(I+SNRs(i)/NT*diag(Gamma)*diag(sigma)));
end
end
C_OL = real(C_OL)/N_iter;
C_CL = real(C_CL)/N_iter;
figure, plot(SNRs_dB, C_OL,'-o', SNRs_dB, C_CL,'-<');
xlabel('SNR [dB]');
ylabel('bps/Hz');
set(gca,'fontsize',10);
legend('Channel Unknown','Channel Known');
title('开环和闭环MIMO信道容量')
grid on

%-----------------------频域注水法-------------------%
%-----------------------author:lzx-------------------------%
%-----------------------date:09点34分-----------------%
function [gamma] = WaterFilling(H, rank, SNR, nT)
% 输入
% H：MIMO信道
% rank: 信道秩的大小
% SNR：信噪比
% nT:发射天线个数
% 输出
% gamma，注水法生成的系数
sigma = svd(H'*H);
% H'*H的奇异值，因为是艾爾特弥矩阵，奇异值和特征值相等
gamma = zeros(1, rank); % 注水法生成的gamma
index = 1:rank;
% 使用的天线的编号,初始化为全都使用
p=1;
while
p < rank
index_used = [1:rank-p+1].';
% 被使用的天线的个数
temp= sum(1./sigma(index(index_used)));
mu = nT/(rank-p+1.)*(1+1/SNR*temp); % 计算mu
gamma(index(index_used)) = mu-nT./(SNR*sigma(index(index_used)));
% 计算gamma
if min(gamma(index))<0
%如果有＜0的结果，这个天线信道应该放弃使用，而把功率重新分配
i=find(gamma==min(gamma)); % 找到＜0的index
ii=find(index==i);
% 去除这个天线
index_new=[index([1:ii-1]) index([ii+1:end])];
clear index;
index=index_new;
p=p+1;
clear gamma;
gamma = zeros(1, rank);
else
p=rank;
% 没有的时候就结束
end
end

一些思考

这是我一直想做的一个仿真了首先要清楚

1. Hiid = sqrt(1/2)(randn(NT,NR) + 1jrandn(NT,NR)); % 生成一个独立同分布H
   H = Rrx(1/2)*Hiid*Rtx(1/2); % 窄带信道

这表明所有的MIMO信道都考虑窄带的，他和时延无关，这从第三章也可以看到，这把问题大大简化了

2. 注水法的代码实现

我自己进行了一些修改，在注释中也说的很清楚了，大致思路就是先按公式分配好，如果有小于0的去除该信道再按公式重新分配直到没有小于零的系数为止。

3. 为什么Rtx和Rrx是这样的矩阵，这是什么模型？

我没有弄清楚，希望有大佬能给我解答

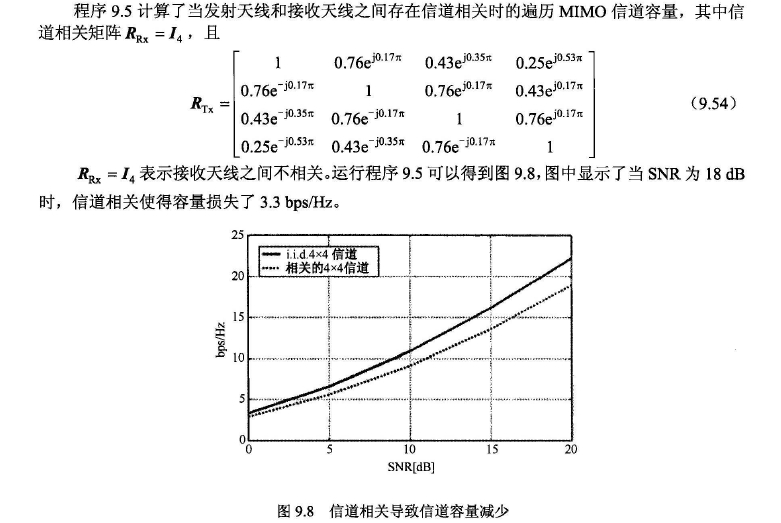
4. 相关系数对信道容量的影响

代码展示

%------------------相关性对信道容量的影响----------------%
%-----------------------author:lzx-------------------------%
%-----------------------date:22点07分-----------------%
clear;
close;
SNR_dB=[0:5:20];
SNR_linear=10.^(SNR_dB/10);
N_iter=1000;
N_SNR=length(SNR_dB);
%%----------------- 4x4 -----------------------------
nT=4;
nR=4;
n=min(nT,nR);
I = eye(n);
sq2=sqrt(0.5);
R=[1
0.76*exp(0.17j*pi)
0.43*exp(0.35j*pi)
0.25*exp(0.53j*pi);
0.76*exp(-0.17j*pi)
1
0.76*exp(0.17j*pi)
0.43*exp(0.35j*pi);
0.43*exp(-0.35j*pi)
0.76*exp(-0.17j*pi)
1
0.76*exp(0.17j*pi);
0.25*exp(-0.53j*pi)
0.43*exp(-0.35j*pi)
0.76*exp(-0.17j*pi)
1
];
C_44_iid=zeros(1,N_SNR);
C_44_corr=zeros(1,N_SNR);
for iter=1:N_iter
H_iid = sq2*(randn(nR,nT)+1j*randn(nR,nT));
H_corr = H_iid*R^(1/2);
tmp1 = H_iid'*H_iid/nT;
tmp2 = H_corr'*H_corr/nT;
for i=1:N_SNR
C_44_iid(i) = C_44_iid(i) + log2(det(I+SNR_linear(i)*tmp1));
%近似公式，见书（9.49）
C_44_corr(i) = C_44_corr(i) + log2(det(I+SNR_linear(i)*tmp2));
end
end
C_44_iid = real(C_44_iid)/N_iter;
C_44_corr = real(C_44_corr)/N_iter;
plot(SNR_dB,C_44_iid, SNR_dB,C_44_corr,':');
xlabel('SNR [dB]');
ylabel('bps/Hz');
set(gca,'fontsize',10)
legend('iid 4x4 channels','correlated 4x4 channels');
title('信道相关信道容量')
grid on;

一些思考

这个仿真弄清楚前面的介绍就非常简单了，所以我几乎没有做什么修改，可以看一下这个程序的前提假设

最后

以上就是辛勤夕阳为你收集整理的初识MIMO（二）：MIMO的信道容量及其仿真初识MIMO（二）：MIMO的信道容量一. SVD简介二.确定性MIMO的信道容量三. 随机MIMO信道容量四.MIMO信道仿真的全部内容，希望文章能够帮你解决初识MIMO（二）：MIMO的信道容量及其仿真初识MIMO（二）：MIMO的信道容量一. SVD简介二.确定性MIMO的信道容量三. 随机MIMO信道容量四.MIMO信道仿真所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。