前言

这一节是对上一篇文章的拓展，不必具体掌握，了解PCA还有这些用途即可。
使用PCA主成分分析不仅能够实现降维操作，还能够实现对数据的降噪操作。
这就使得，通过pca降噪之后，不仅运算速度提升了，对样本的识别率可能也会随之提升，同时pca在人脸识别领域也有相应的应用

一、PCA 降噪

如我们上一篇中的数据，我们自动添加了噪音，绘制出来的图像如图：

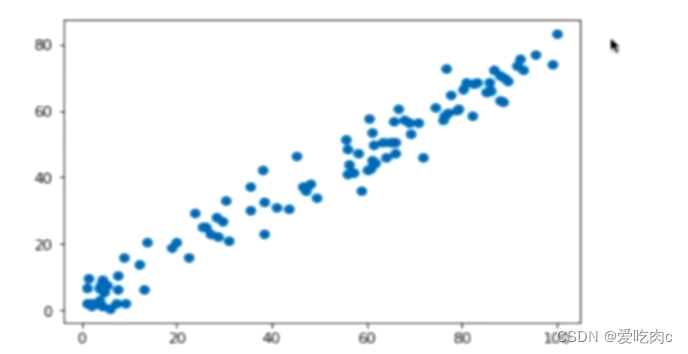
那么在求出第一主成分之后，绘制出来的图像为：

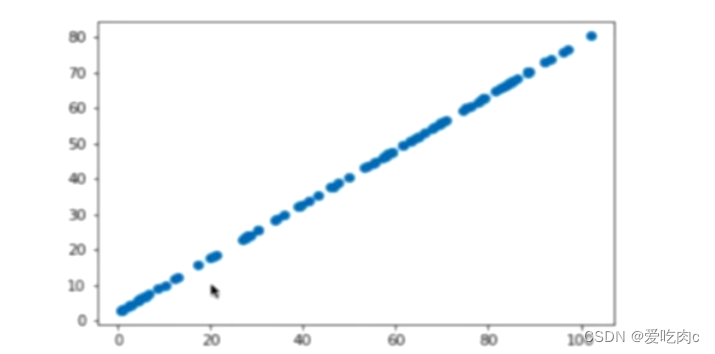
我们可以理解为求出主成分之后的图像进行了降维同时也丢失了成分
但是是否该降维后的图形才是真实的数据呢？
是否可以理解为降维之后的数据是进行了去噪处理呢？
因为现实世界中的数据可能测量方法或仪器有误差。这很难说。

所以PCA不仅可以降维同时也可以去噪。

二、特征脸

1、原理

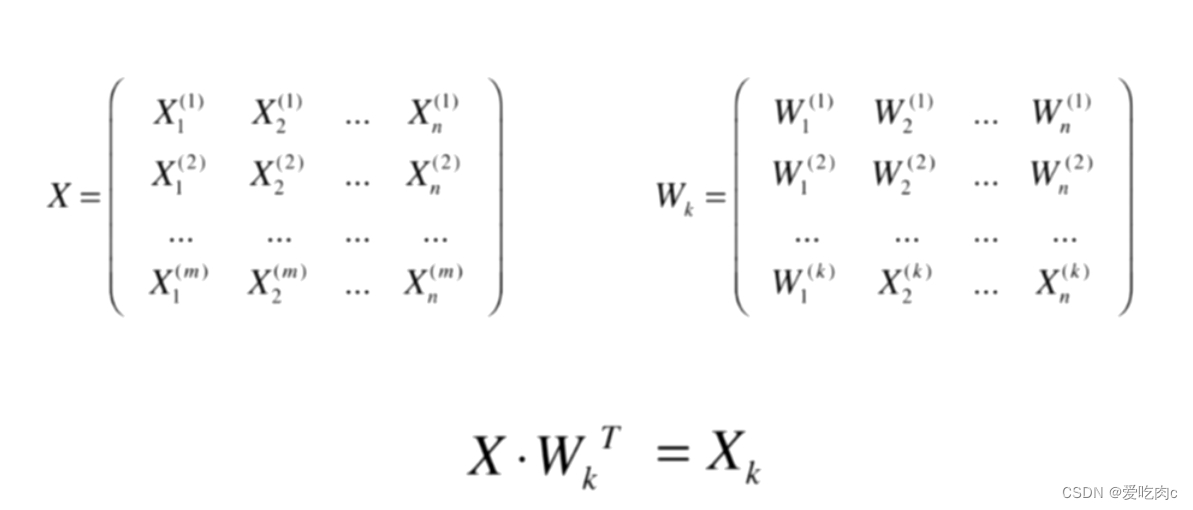
如X这个矩阵 是m行n列 即每个样本有n个特征
如让X与WK的转置 点乘 即得到X在前k个主成分上的映射
但我们也可以把求出的前k个主成分 也看成一个个样本 它也是n列的
那么此时 第一个主成分就是包含我们数据X信息最多的那个样本
也可以称为特征脸

2.下载数据

from sklearn.datasets import fetch_lfw_people

faces=fetch_lfw_people()

因为这个出现了很多错误
在这里分享一个解决方法

点击这里 我是看这篇文章解决的~

3、代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people

faces=fetch_lfw_people()
faces.keys()
random_indexs=np.random.permutation(len(faces.data))  #打乱顺序 随机取
x=faces.data[random_indexs]
example_faces=x[:36] #取前三十六张图片
#绘制脸的函数
def plot_faces(faces):
    fig,axes=plt.subplots(6,6,figsize=(10,10),
                         subplot_kw={'xticks':[],'yticks':[]},
    gridspec_kw=dict(hspace=0.1,wspace=0.1))
    for i,ax in enumerate(axes.flat):
        ax.imshow(faces[i].reshape(62,47),cmap='bone')
    plt.show()
plot_faces(example_faces)

结果：

求所有图片的主成分 因为共有2914的样本特征，所以主成分也有2914

from sklearn.decomposition import PCA
%%time 
pca=PCA(svd_solver='randomized')
pca.fit(x)
plot_faces(pca.components_[:36,]) #绘制前36个主成分 即特征脸

我们可以看到第一主成分即可表现人脸的大致轮廓

最后

以上就是妩媚大雁为你收集整理的PCA拓展---去噪，人脸识别（特征脸）前言一、PCA 降噪二、特征脸的全部内容，希望文章能够帮你解决PCA拓展---去噪，人脸识别（特征脸）前言一、PCA 降噪二、特征脸所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。