一、前言
前天看了一篇博客介绍A*算法，按照自己的理解记录一下A*算法。
二、应用场景
一副地图中有坐标A和B，需要找到一条路径（如果有的话）能从A到B，地图中可能有河流或墙壁不能直接穿过，我们需要怎样找到这条路径呢？
在我们以往学习到的路径寻找中，我们可以想到广度优先搜索（BFS：Breadth First Search）和深度优先搜索（DFS：Depth-First-Search） 进行路径寻找。先看一下广度优先搜索如下图（图片来源网上）。BFS以起点A为圆心，先搜索A周围的所有点，形成一个类似圆的搜索区域，再扩大搜索半径，进一步搜索其它没搜索到的区域，直到终点B进入搜索区域内被找到。
再看一下深度优先搜索，这里的深度优先搜索不是所有路径都搜索而是沿着B点方向搜索。（图片来源网上）。DFS则是让搜索的区域离A尽量远，离B尽量近，比如现在你在一个陌生的大学校园里，你知道校门口在你的北方，虽然你不知道你和校门口之间的路况如何，地形如何，但是你会尽可能的往北方走，总能找到校门口。
比起BFS，DFS因为尽量靠近终点的原则，其实是用终点相对与当前点的方向为导向，所以有一个大致的方向，就不用盲目地去找了，这样，就能比BFS能快地找出来最短路径，但是这种快速寻找默认起点A终点B之间没有任何障碍物，地形的权值也都差不多。如果起点终点之间有障碍物，那么DFS就会出现绕弯的情况。
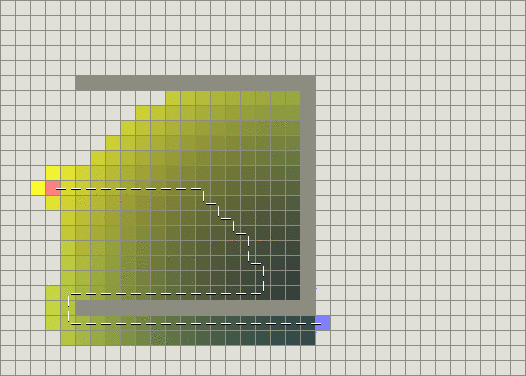
图中DFS算法使电脑一路往更右下方的区域探索，可以看出，在DFS遇到障碍物时，其实没有办法找到一条最优的路径，只能保证DFS会提供其中的一条路径（如果有的话）。
大概了解了BFS和DFS，对比这两者可以看出来，BFS保证的是从起点到达路线上的任意点花费的代价最小（但是不考虑这个过程是否要搜索很多格子）；DFS保证的是通过不断矫正行走方向和终点的方向的关系，使发现终点要搜索的格子更少（但是不考虑这个过程是否绕远）。
A*算法的设计同时融合了BFS和DFS的优势，既考虑到了从起点通过当前路线的代价（保证了不会绕路），又不断的计算当前路线方向是否更趋近终点的方向（保证了不会搜索很多图块），是一种静态路网中最有效的直接搜索算法。
闲谈：我们知道BFS和DFS，但将这两种思想融会贯通，创造一种新的解决问题方法（A*算法），这在思路太棒了。膜拜学习。
三、A*算法
3.1 思想
A*算法运用的是估价思想。查找过程：
- 在待遍历列表中（刚开始只有点A），我们在列表中查找一个估价（当前点到终点距离估价，后续会讲）最小的点（k），
- 对点k进行一次广度优先查找，也就是它移动一次到底的下一个坐标（右，右上，上，左上，左，左下，下，右下）不包含已经遍历过的点和不能到达的点，将能查找的点添加到队列中，并将点K从队列中移除。
- 重复1、2步骤直到到底B点，或者队列已经为空说明没有路径可以到达点B。
运用的思想：先进行一次DFS搜索再进行一次BFS搜索，循环这个过程直到找到目标点B。
过程1：运用DFS思想，尽量找离B近的点（也就是估值最小的点）。
过程2：运用BFS思想，以点K为圆心，搜索A周围的所有还未搜索的点。
3.2 怎样估价
3.2.1 公式：F = G + H。
G = 从起点 A 移动到指定方格的移动代价，沿着到达该方格而生成的路径。我们约定直行移动一次代价是10，对角线的移动代价为 14。（实际对角移动距离是 2 的平方根，或者是近似的 1.414 倍的横向或纵向移动代价）。
H = 从指定的方格移动到终点 B 的估算成本。计算从当前方格横向或纵向移动到达目标所经过的方格数，忽略对角移动，然后把总数乘以 10 。
3.2.2 计算
我们设当前点为K
H 值很容易计算，H = （两个点横坐标距离 + 两个点纵坐标距离） X 10
G 值计算，计算K到A的最小估价我们只需要计算K点的周围八个点（可以被访问且已经被访问点）的g值+到K点的移动代价，其中最小估价即为K点的g值，这个点我们称为K点的父节点。k点正在访问，那么它周围至少有一个点已经被访问了。
3.2.2 约定
在一个方格中我们将FGH标记在它的左上，左下和右下三个位置，以便我们观察每次估价的结果。
箭头指向的是它父节点的坐标，后续找路线需要用到。
3.3 实例演示一 无障碍物 （对应编码实现中测试用例9）
说明：坐标访问和父节点查找约定顺序：右，右上，上，左上，左，左下，下，右下，沿X轴增加的方向为右，沿Y轴增加的方向为上，父节点可能会有多个，这里选择代价最小最后搜索的为父节点。
坐标A(2，2)，目标坐标B(6，3)，已经对坐标A进行了估值。
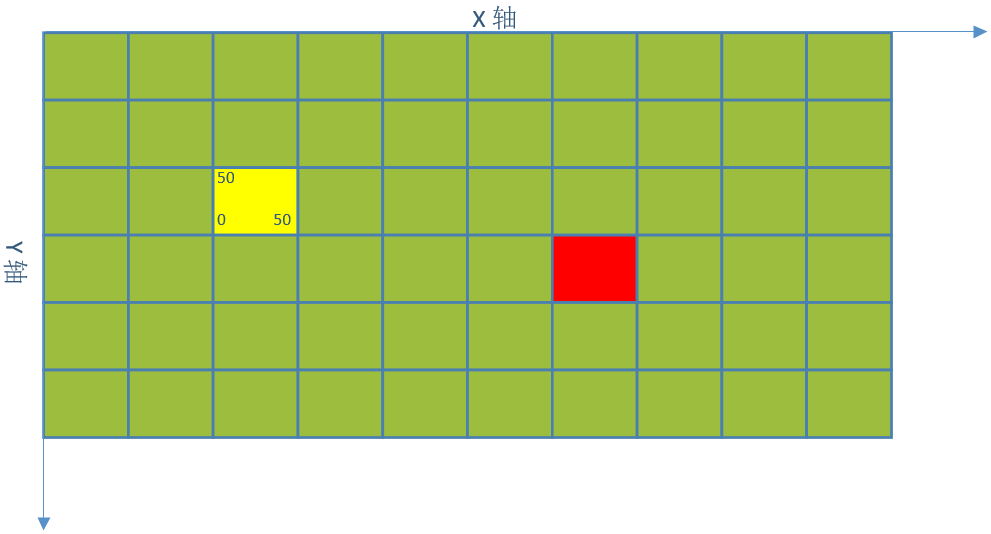
1. 对点（2，2）八个方向的坐标进行估值，它们的父节点都是（2，2），最小估值坐标紫色（3，3），标记紫色只是为了方便下一次寻找。估值顺序我们约定（右，右上，上，左上，左，左下，下，右下），此后我们都按照这个顺序进行。
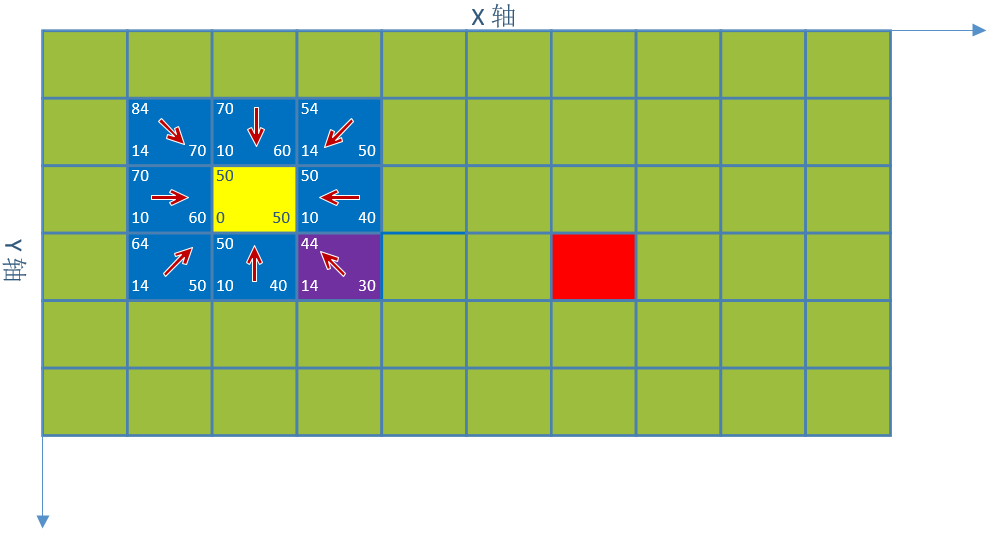
2. 对点（3，3）八个方向的坐标进行估值（已经估值的不用再计算），我们称已经估值的点为已经被访问，最小估值坐标紫色（4，3）。父节点搜索顺序约定（右，右上，上，左上，左，左下，下，右下），g值最小最后访问的点为父节点。如下图。这个图我们需要理解箭头是怎样确定的。例如点（4，3）它的父节点既可以是点（3，3）也可以是点（3，2），访问顺序是先访问点（3，3）后访问点（3，2）所以我们把点（3，2）作为点（4，3）的父节点。
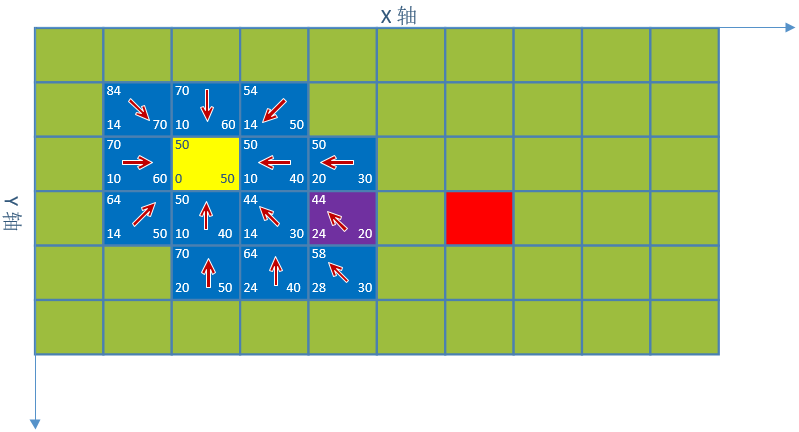
3. 对点（4，3）继续寻找，最小估值坐标紫色（5，3）
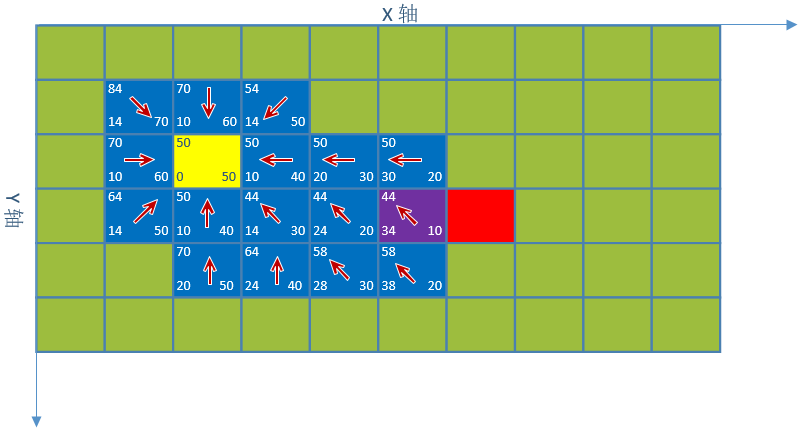
4. 对点（5，3）继续寻找，搜索到了终点，停止搜索
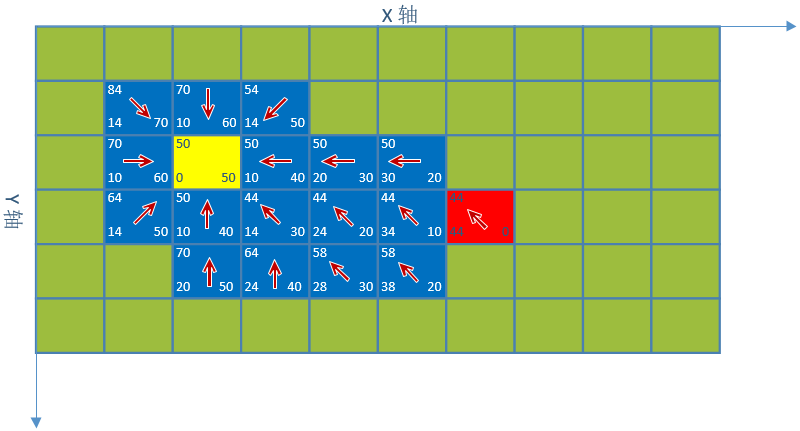
5. 通过终点依次查找它们的父节点直到起点，然后将坐标点逆序，就是我们要的路线了。
路线：（2，2）、（3，2）、（4，2）、（5，2）、（6，3）
3.4 实例演示二 有障碍物 （对应编码实现中测试用例10）
有无障碍物处理是一样的。
坐标A(2，2)，目标坐标B(6，3)，已经对坐标A进行了估值。其中坐标（4，1）、（4，2）、（4，3）无障碍物不能访问
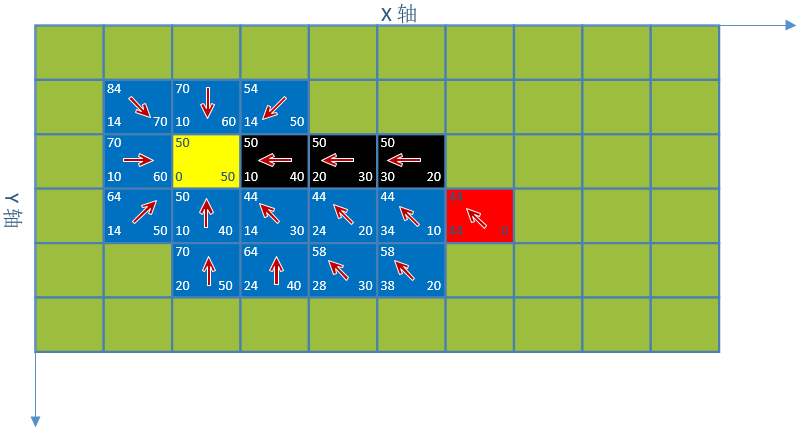
1. 对点（2，2）八个方向的坐标进行估值，它们的父节点都是（2，2），最小估值坐标紫色（3，3）
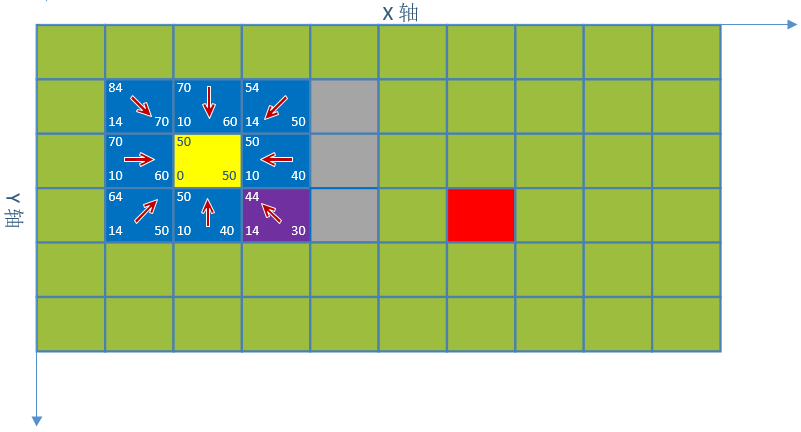
2. 对点（3，3）继续寻找，最小估值坐标紫色（2，3）
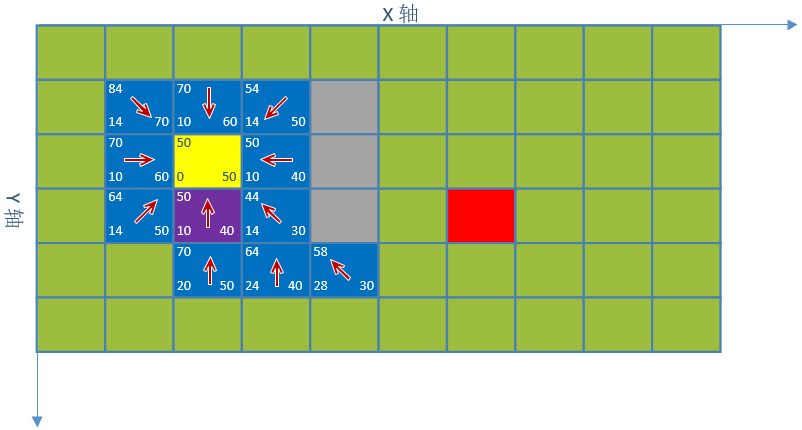
3. 对点（3，2）继续寻找，最小估值坐标紫色（4，4）
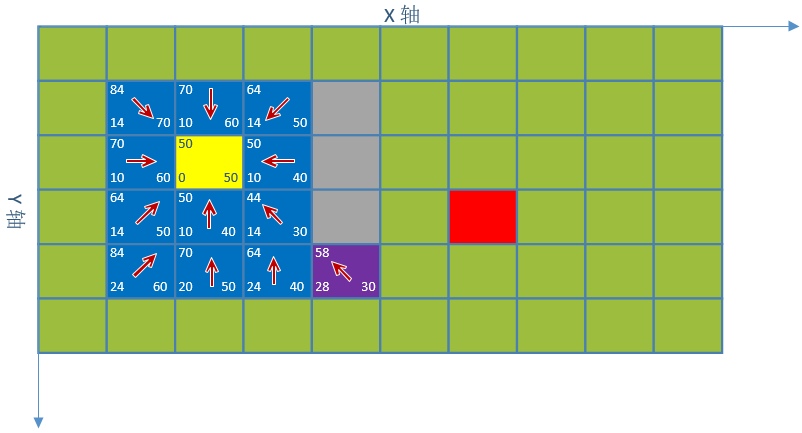
4. 对点（4，4）继续寻找，最小估值坐标紫色（5，3）
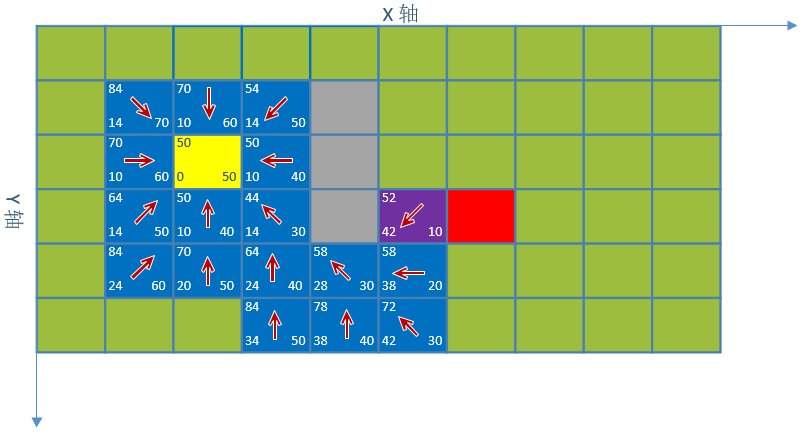
5. 对点（5，3）继续寻找，搜索到了终点，停止搜索
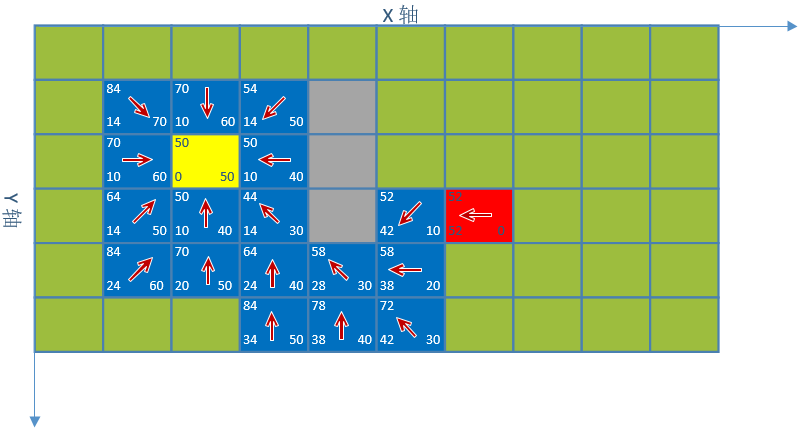
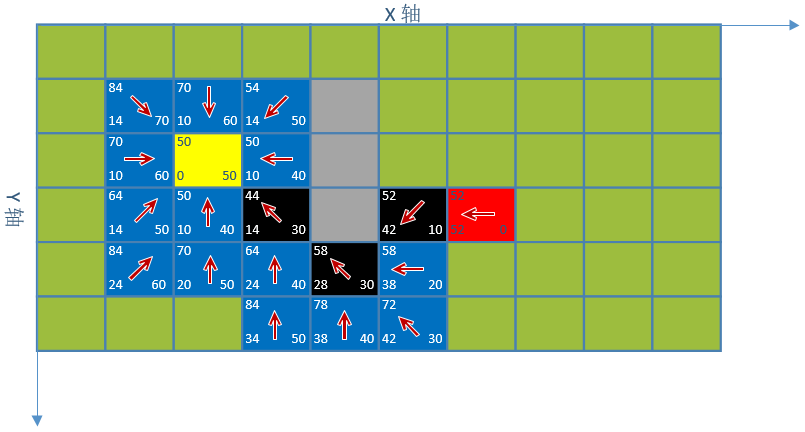
6. 通过终点依次查找它们的父节点直到起点，然后将坐标点逆序，就是我们要的路线了。
路线：（2，2）、（3，3）、（4，4）、（5，3）、（6，3）
四、编码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421//========================================================================== /** * @file : Astar.h * @author : niebingyu * @title : A*算法 * @purpose : A*算法实现 * * 博客：https://blog.csdn.net/nie2314550441/article/details/106733189 */ //========================================================================== #pragma once #include <assert.h> #include <vector> #include <list> #include <iostream> #include <queue> using namespace std; #define NAMESPACE_ASTAR namespace NAME_ASTAR { #define NAMESPACE_ASTAREND } NAMESPACE_ASTAR #define GET_ARRAY_LEN(array) (sizeof(array)/sizeof(array[0])) struct Point { int x; // 宽 int y; // 高 Point(int tx = 0, int ty = 0) : x(tx), y(ty) {} // 两个坐标距离：横坐标距离 + 纵坐标距离 int operator - (const Point& p) { return abs(x - p.x) + abs(y - p.y); } bool operator == (const Point& p) { return x == p.x && y == p.y; } }; struct PointV : public Point { int value; // 0 :无障碍; 1:有障碍 PointV(int nx = 0, int ny = 0, int v = 0) : Point(nx, ny), value(v) {} }; struct PointAStart : public Point { int f, g, h; bool visited; // 是否被访问过，0：未被访问，1已经被访问 Point parentNode; PointAStart(int tf = 0, int tg = 0, int th = 0, int tx = 0, int ny = 0) : Point(tx, ny), f(tf), g(tg), h(th), visited(false), parentNode() {}; bool operator < (const PointAStart& t) { return f < t.f; } void SetFGH(int tf, int tg, int th) { f = tf; g = tg, h = th; } }; // 重写仿函数, 优先队列元素大小比较 struct comp //重写仿函数 { bool operator() (PointAStart* a, PointAStart* b) { return a->f > b->f; //小顶堆 } }; // A* 算法 class AStar { public: // arr 是一个二维数组 // s 起点; e 终点 vector<Point> operator()(const vector<vector<int>>& arr, Point s, Point e) { if (arr.empty() || s == e) return {}; int lenY = (int)arr.size() - 1; // 高 int lenX = (int)arr[0].size() - 1; // 宽 if (s.x > lenX || s.y > lenY || e.x > lenX || e.y > lenY) return {}; if (arr[s.y][s.x] != 0 || arr[e.y][e.x] != 0) return {}; for (int i = 0; i < lenY; ++i) assert(lenX == (int)arr[i].size() - 1); vector<vector<PointAStart>> pArr(lenY + 1, vector<PointAStart>(lenX + 1)); // 父结点 priority_queue<PointAStart*, vector<PointAStart*>, comp> openList; // by 2020/07/30 改用优先队列 int g = 0, h = (s - e) * 10, f = g + h; PointAStart pt(f, g, h, s.x, s.y); pt.visited = true; pArr[s.y][s.x] = pt; openList.push(&pArr[s.y][s.x]); bool seek = true; const int dirs[8][3] = { {0,1,10},{1,1,14},{1,0,10},{1,-1,14},{0,-1,10},{-1,-1,14},{-1,0,10},{-1,1,14} };//8个移动方向（右，右上，上，左上，左，左下，下，右下） while (seek && !openList.empty()) { PointAStart& p = *openList.top(); openList.pop(); p.visited = true; for (int i = 0; i < GET_ARRAY_LEN(dirs) && seek; ++i) { Point t(p.x + dirs[i][1], p.y + dirs[i][0]); // t 需要未被访问 if (t.x < 0 || t.x > lenX || t.y < 0 || t.y > lenY || arr[t.y][t.x] == 1 || pArr[t.y][t.x].visited) continue; // 找父节点 g = p.g + dirs[i][2]; h = (t - e) * 10; f = g + h; int minf = f; PointAStart newPoint(f, g, h, t.x, t.y); newPoint.visited = 1; newPoint.parentNode.x = p.x; newPoint.parentNode.y = p.y; for (int j = 0; j < GET_ARRAY_LEN(dirs); ++j) { Point pp(t.x + dirs[j][1], t.y + dirs[j][0]); //父节点Parent Point // 父节点pp, 在需要已经被访问 if (pp.x < 0 || pp.x > lenX || pp.y < 0 || pp.y > lenY || arr[pp.y][pp.x] == 1 || !pArr[pp.y][pp.x].visited) continue; g = pArr[pp.y][pp.x].g + dirs[j][2]; f = g + h; if (f <= minf) { minf = f; f = g + h; newPoint.SetFGH(f, g, h); newPoint.parentNode = pp; } } pArr[t.y][t.x] = newPoint; openList.push(&pArr[t.y][t.x]); if (t == e) seek = false; } } if (!pArr[e.y][e.x].visited) { cout << "无法到达" << endl; return {}; } else { vector<Point> path; path.push_back(e); Point p = pArr[e.y][e.x].parentNode; while (true) { if (!pArr[p.y][p.x].visited) { cout << "无法到达" << endl; return {}; } path.push_back(p); if (p == s) break; p = pArr[p.y][p.x].parentNode; } reverse(path.begin(), path.end()); SetVisitedCount(pArr); // 辅助测试，记录访问的结点数 return path; } } // 辅助测试，用于获取访问的结点数 void SetVisitedCount(const vector<vector<PointAStart>>& pArr) { visitCount = 0; for (int i = 0; i < pArr.size(); ++i) { for (int j = 0; j < pArr[i].size(); ++j) { if (pArr[i][j].visited) ++visitCount; } } } int visitCount; }; // // 测试 用例 START void test(const char* testName, const vector<vector<int>>& arr, Point s, Point e) { AStar as; vector<Point> result = as(arr, s, e); cout << testName << "[" << as.visitCount << ", " << result.size() << "]"; for (int i = 0; i < result.size(); ++i) { cout << ", (" << result[i].x << "," << result[i].y << ")"; } cout << endl; } // 测试用例 void Test1() { vector<vector<int>> arr = { {0,0}, }; Point s(0, 0); Point e(1, 0); test("Test1()", arr, s, e); } void Test2() { vector<vector<int>> arr = { {0}, {0} }; Point s(0, 0); Point e(0, 1); test("Test2()", arr, s, e); } void Test3() { vector<vector<int>> arr = { {0,0,}, {0,0,}, }; Point s(0, 0); Point e(1, 1); test("Test3()", arr, s, e); } void Test4() { vector<vector<int>> arr = { {0,0,0,}, {0,0,0,}, }; Point s(0, 0); Point e(2, 1); test("Test4()", arr, s, e); } void Test5() { vector<vector<int>> arr = { {0,1,0,}, {0,1,0,}, {0,0,0,}, }; Point s(0, 0); Point e(2, 0); test("Test5()", arr, s, e); } void Test6() { vector<vector<int>> arr = { {0,0,0,0,0,0,0,0}, {0,0,0,0,1,0,0,0}, {0,0,0,0,1,0,0,0}, {0,0,0,0,1,0,0,0}, {0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0}, }; Point s(2, 2); Point e(6, 2); test("Test6()", arr, s, e); } void Test7() { vector<vector<int>> arr = { {0,0,0,0,0,0,0,0}, {0,0,0,0,1,0,0,0}, {0,0,0,0,1,0,0,0}, {0,0,0,0,1,0,0,0}, {0,0,0,0,1,0,0,0}, {0,0,0,0,1,0,0,0}, }; Point s(2, 2); Point e(6, 2); test("Test7()", arr, s, e); } void Test8() { vector<vector<int>> arr = { {0,0,0,0,0,0,0,0,0}, {0,0,0,0,1,1,1,1,0}, {0,0,0,0,1,0,0,1,0}, {0,0,0,0,1,0,0,1,0}, {0,0,0,0,1,0,1,1,0}, {0,0,0,0,1,0,0,0,0}, }; Point s(2, 2); Point e(6, 2); test("Test8()", arr, s, e); } void Test9() { vector<vector<int>> arr = { {0,0,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,0,0}, }; Point s(2, 2); Point e(6, 3); test("Test9()", arr, s, e); } void Test10() { vector<vector<int>> arr = { {0,0,0,0,0,0,0,0,0,0}, {0,0,0,0,1,0,0,0,0,0}, {0,0,0,0,1,0,0,0,0,0}, {0,0,0,0,1,0,0,0,0,0}, {0,0,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,0,0}, }; Point s(2, 2); Point e(6, 3); test("Test10()", arr, s, e); } void Test11() { vector<vector<int>> arr = { {0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}, {0,1,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}, {0,1,0,0,1,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0}, {0,1,0,0,1,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0}, {0,1,0,0,1,0,0,0,1,0,0,0,0,1,0,0,1,1,1,0,0,0,0,0,0,0,0}, {0,1,0,0,1,0,0,0,1,0,0,0,0,1,0,0,1,0,1,0,0,0,0,0,0,0,0}, {0,1,0,0,1,0,0,0,1,0,0,0,0,1,0,0,1,0,1,0,0,0,0,0,0,0,0}, {0,1,0,0,1,0,0,0,1,0,0,0,0,1,0,1,1,0,1,0,0,0,0,0,0,0,0}, {0,1,1,1,1,0,0,0,1,0,0,0,0,1,0,1,0,0,1,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,1,0,0,0,0,1,0,1,0,0,1,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,1,0,0,0,0,1,0,1,0,0,1,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,1,0,0,0,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0}, {0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0}, }; Point s(2, 7); Point e(17, 5); test("Test11()", arr, s, e); } NAMESPACE_ASTAREND // 测试 用例 END // void AStar_Test() { #if 1 NAME_ASTAR::Test1(); NAME_ASTAR::Test2(); NAME_ASTAR::Test3(); NAME_ASTAR::Test4(); NAME_ASTAR::Test5(); NAME_ASTAR::Test6(); NAME_ASTAR::Test7(); NAME_ASTAR::Test8(); NAME_ASTAR::Test9(); NAME_ASTAR::Test10(); NAME_ASTAR::Test11(); #endif //NAME_ASTAR::Test9(); }
执行结果：
五、拓展
5.1 如果现在需求有变，不能沿对角线移动，也就是只能上下左右移动，需要怎样实现呢？
修改第82行代码 const int dirs[8][3] = { {0,1,10},{1,1,14},{1,0,10},{1,-1,14},{0,-1,10},{-1,-1,14},{-1,0,10},{-1,1,14} };//8个移动方向（右，右上，上，左上，左，左下，下，右下）
改为 const int dirs[4][3] = { {0,1,10},{1,0,10},{0,-1,10},{-1,0,10} };//8个移动方向（右，上，左，下）
5.2 需求再变动一下，只能沿着上下左右移动，但向右可以一次移动1格或者2格，需要怎样实现呢？
同理修改第82行代码 const int dirs[8][3] = { {0,1,10},{1,1,14},{1,0,10},{1,-1,14},{0,-1,10},{-1,-1,14},{-1,0,10},{-1,1,14} };//8个移动方向（右，右上，上，左上，左，左下，下，右下）
改为 const int dirs[5][3] = { {0,1,10}, {0,2,20},{1,0,10},{0,-1,10},{-1,0,10} };//8个移动方向（右1格，右2格，上，左，下）
六、闲谈
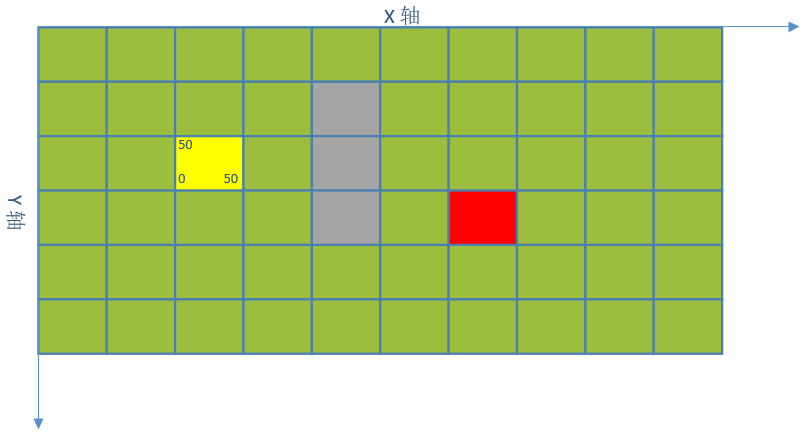
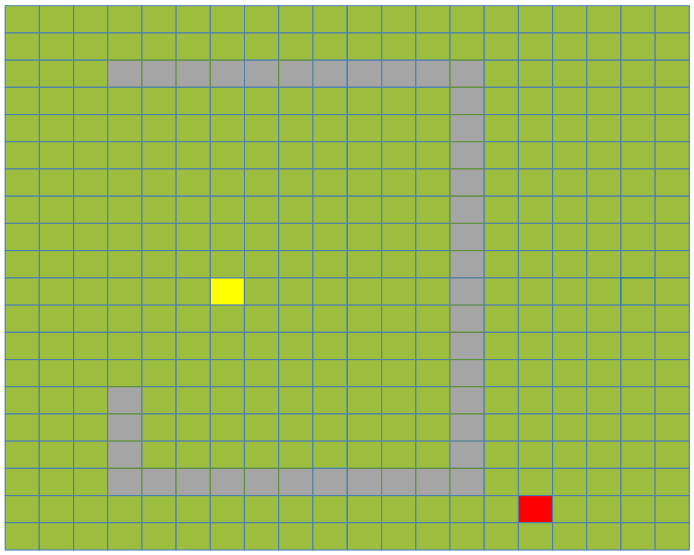
前面我们介绍的都是起点去找终点，观察一下下面这种情况，黄色是起点，红色是终点。起点找终点会搜索大量无用的坐标点，而如果是终点去寻找起点搜索需要坐标点会少很多。那我们可不可以起点和终点一起去寻找对方呢？
参考：A*算法详解_聂炳玉的博客-CSDN博客_a*算法
A*寻路算法的探寻与改良（一） - 知乎
2020/6/14 补充说明
六、延伸扩展
已经知道A*算法过程，再逆序思索一下这个算法。起点A，终点B，假设存在一条最优的路线能从A到B。
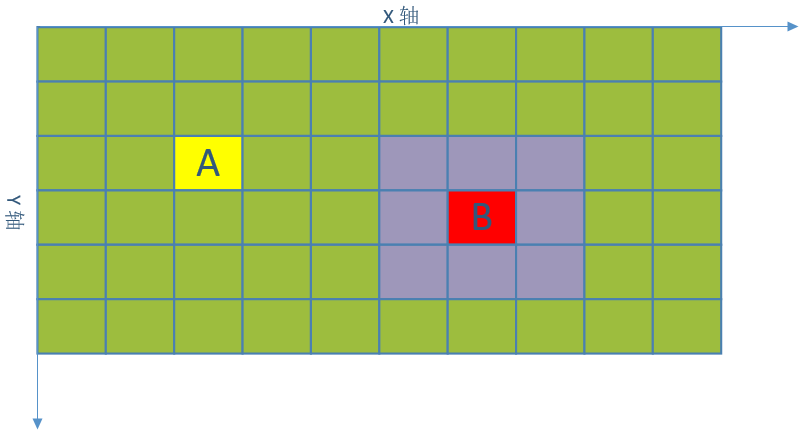
我们继续观察这个图，如果存在最优路线。到达B的上一个坐标点一定是B点周围的一个坐标称之为父节点。也就是我们只需要找到这个点父节点。这种思路不就是动态规划中的自顶向下。自顶向下效率不佳，我们将其转换成自底向上求解就可以了。我们在求解动态规划问题往往都是计算最终结果，如果需要求解这个过程是怎样的呢？
A*算法就是这个问题的自底向上求解的过程。A*算法给我们提供了一个很好的思路，我们只需要记录当前结果产生的父节点，通过父节点倒推这个过程。例如《算法导论——钢条切割》需要求解的是最大价值，那最多价值切割的方法是怎样呢？可以通过上面说的方法求解。
可以理解A*算法 是结合了 深度优先、广度优先、以及动态规划的思想。个人理解。
最后
以上就是风趣香烟最近收集整理的关于寻路算法——A*算法详解并附带实现代码的全部内容，更多相关寻路算法——A*算法详解并附带实现代码内容请搜索靠谱客的其他文章。
发表评论 取消回复