目录
- 前言
- 一、数据类型
- 1. 矩阵
- 2. 单元数组
- 3. 结构体
- 4. 数值取整
- 二、数据显示格式
- 三、运算方法和求积分
- 四、求解微分方程和函数最小值及零点
- 1. 求通解
- 2. 求特解
- 3. 求微分方程组
- 4. 求函数最小值和零点
- 4. 求函数零点
- 五、矩阵升级操作
- 六、逻辑及流程控制
- 1.if...else...end
- 2. for...end
- 3. while...end
- 3. switch...case...end
- 八、文件导入
- 1. mat格式
- 2. txt格式
- 3. xls格式
- 4. csv格式
- 九、随机数的产生
- 1. 二项分布随机数
- 2. 泊松分布随机数
- 3. 均匀分布随机数
- 4. 正态分布
- 十、MATLAB绘图
前言
MATLAB有一些语法和我们常用的python、C++、C等编译语言的语法有所不同，比如MATLAB中的注释使用%而不是/*，但就我个人的使用来说，我认为MATLAB的语法还是更简洁方便的，像python一样，一行语句结束后不需要加分号。
它的功能十分强大，包含很多很多库函数，也可以轻松地实现图形化和可视化，最重要的是使用MATLAB画出的图非常的好看，我们也可以对图像进行处理分析，对用户非常友好。
编者是要参加数学建模比赛，所以想要学一学MATLAB，但对于我这个专业，学习MATLAB也有很大帮助，MATLAB可以与Simulink结合使用，对机器人的控制系统、电气系统以及机器人的运动方式进行仿真，我先学着MATLAB的基本知识，以后或许也会学习使用MATLAB进行仿真。
一、数据类型
MATLAB的数据类型主要有五种：
- 数字类型
- 字符与字符串
- 矩阵
- 单元数组
- 结构体
其中一些数据结构我们已经习以为常了，我就不再介绍了，主要介绍一下一些专有的数据结构。
1. 矩阵
创建矩阵的方式有两种：直接赋值创建和使用函数创建。
示例如下：
1
2
3
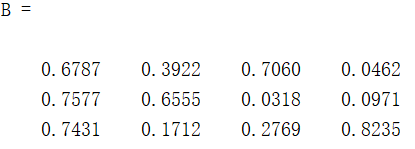
4% 矩阵 A = [1,2,3;4,5,6;7,8,9] %直接赋值创建 B = rand(3,4) %创建一个3行4列的随机矩阵，每个位置都是0到1之间的数
结果如下：
矩阵的操作也很丰富，MATLAB可以轻易地实现矩阵的转置、矩阵的逆、将矩阵排成一列、矩阵相乘等操作。
实例如下：
1
2
3
4
5C = A' %矩阵的转置 D = inv(A) %矩阵的逆 E = A(:) %将矩阵元素排成一列 A * D %矩阵相乘
结果如下：
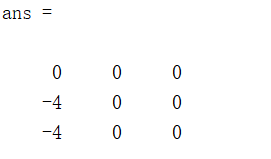
如果矩阵是复数，在转置操作时略有不同，这一部分在电路中可能会用到，比如PID
示例如下：
1
2
3
4
5
6
7%% 复数矩阵的转置 clear all A = [4+3i 5+6i 7+i] B = A' %共轭转置 B2 = A.' %位置转置
结果如下：
同时，如果我们的矩阵的行和列很多，在命令行中无法完全查看到，我们也可以对矩阵进行一些查看的操作。
示例如下：
1
2
3rows = size(A,1) %查看矩阵行数 cols = size(A,2) %查看矩阵列数
结果如下：
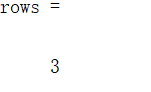
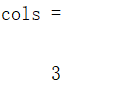
矩阵块操作：
1
2
3
4
5
6
7%% 矩阵的块操作 clc clear all A = magic(2) B = repmat(A,2,3)
结果如下：
将多个矩阵作为对角块产生新矩阵
示例如下：
1
2
3
4
5
6
7%% 将多个矩阵作为对角块产生新的矩阵 clear all A = magic(3) B = [1:2;3:4] C = blkdiag(A,B)
结果如下：
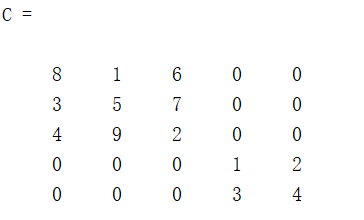
矩阵的旋转也是很重要的一部分，在机器人的位姿变换中用处很大。
示例如下：
1
2
3
4
5
6
7%% 逆时针旋转90度的K倍，默认为1倍 clear all A = rand(2,3) B = rot90(A) %逆时针旋转90度的1倍 C = rot90(A,2) %逆时针旋转90度的2倍
结果如下：
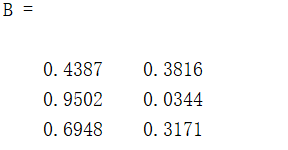
矩阵翻转
1
2
3
4
5
6
7
8%% 矩阵翻转 clear all A = rand(2,2) B = fliplr(A) %左右翻转 C = flipud(A) %上下翻转 D = flipdim(A,1) %指定方向翻转，1为左右，2为上下 E = flipdim(A,2)
结果如下：
2. 单元数组
创建单元数组的方法也是有两种：直接创建和使用cell函数创建
示例如下：
1
2
3
4
5% 单元数组 clear all %清空所有变量 A = cell(1,6) %创建一个1行6列的单元数组 B = {'haha','哈哈';[7,5,6],88} %直接创建一个单元数组
结果如下：
对于单元数组，我们也可以对其元素进行一些操作，比如单独显示单元数组的元素、对数组进行扩充和删除、图形化显示单元数组元素、赋值等。
示例如下：
1
2
3
4
5
6
7
8
9
10
11clear all; c = {'hhh','shabby';[5,4,6,8,7],7} %创建数组 c{1,1} %查看单元数组元素 c{2,2}=[] %删除操作 % 单独显示单元数组元素 celldisp(c) % 图形化显示单元数组元素 figure out = cellplot(c,'legend')
结果如下：
也可以进行将矩阵转换成单元数组的操作，并判断是否转换成功
示例如下：
1
2
3
4
5
6
7%% 将矩阵转换成单元数组 clear all a = [4 5 2; 4 2 1] c = num2cell(a) %将矩阵转换成单元数组 iscell(c) %判断是否为单元数组
结果如下：
3. 结构体
MATLAB中的结构体和以前编译语言中的定义有所不同，感觉有点抽象…
创建结构体：
1
2
3
4
5
6
7% 结构体 clear all s = struct('figure',{'big','little'},'yanse',{'blue'}) diyi = s(1) %查看所有成员的第一个内容 dier = s(2)
结果如下：
删除成员变量：
1
2
3shan1 = rmfield(s,'figure') %删除figure这个成员变量 shan1and2 = rmfield(s,{'figure','yanse'}) %删除1和2两个成员变量
结果如下：
判断：
1
2
3f1 = isstruct(s) %判断是否为结构体 f2 = isfield(s,'figure') %判断是否为结构体成员
结果如下：
获取成员变量的值：
1
2
3% 获取某个实际成员变量的值 s(1).figure
结果如下：
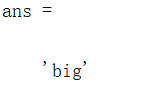
使用函数获取：
1
2
3%使用函数获取成员变量的值 f = getfield(s,'figure')
结果如下：
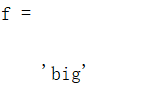
4. 数值取整
整数是一个我们非常常用，也很喜欢的数据类型，MATLAB中数值取整主要有以下几种方法。
示例如下：
1
2
3
4
5r = round(8.5) %四舍五入取整 a = fix(9.9) %向0取整 f = floor(6.8) %向小于等于该数的最近接的整数取整 c = ceil(2.2) %向大于等于该数的最接近整数取整
结果如下：
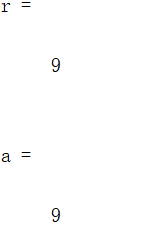
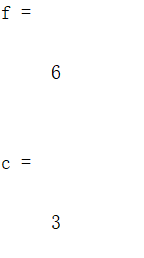
二、数据显示格式
数据显示格式的意思是：改变数据显示格式，但不改变数值，默认保留小数点后四位
示例如下：
1
2
3
4
5
6
7
8
9
10a = 6.32254188 format long a format short a format long e a format short e a
结果如下：
我们也可以将数值转换成逻辑值0或1，转换规则就是只有出现0才会为假，其他数值均为真。
转换时，需要使用函数logical
示例如下：
1
2
3
4
5a = 6.32254188 logical(a) %真值转换 b = 0 logical(b) %假值转换
结果如下：
最后，说一下函数句柄，函数句柄是用来间接调用函数的工具，非常好用！
示例如下：
1
2
3
4f = @cos %创建函数句柄 t = 0:pi/4:pi %t的范围是0到π，以π/4为一个单位 f(t)
结果如下：
对函数句柄也可以进行一些操作，这里只介绍判断函数句柄和检测是否为同一个。
示例如下：
1
2
3isa(f,'function_handle') %判断f是否为函数句柄 isequal(f1,f2) %判断两个函数句柄是否为同一个
结果如下：
三、运算方法和求积分
运算方法和我们以前熟知的编译器相同，我就懒得再整理一遍了，直接讲一些MATLAB使用起来比较方便或者说比较特殊的吧。
积分求解：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31%% 求积分 %% 使用quad函数求积分 单变量数值积分求解 clear all syms x; %设置自变量 f = inline('1./(sin(x)+exp(-x.^2))') %内联函数 y = quad(f,0,1) %积分求解 %% 使用quadl函数求解积分，速度更快，精度更高 clear all syms x f = inline('1./(sin(x)+exp(-x.^2))') y = quadl(f,0,1) %% 双重积分求解 clear all syms x f = inline('x*cos(y)+y*sin(x)','x','y') y = dblquad(f,pi,2*pi,0,pi) %% 三重积分求解 clear all syms x f = inline('x*sin(y)+z','x','y','z') y = triplequad(f,0,1,2,4,5,7)
结果如下：
四、求解微分方程和函数最小值及零点
1. 求通解
示例如下：
1
2
3
4
5%% 求通解 clear all f1 = dsolve('Dy-y=sin(x)') %默认情况下以t为自变量求解 f2 = dsolve('Dy-y=sin(x)') %以x为自变量求解
结果如下：
2. 求特解
示例如下：
1
2
3
4%% 求特解 clear all dsolve('Dy=a*y','y(0)=b')
结果如下：
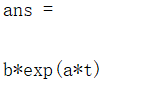
3. 求微分方程组
示例如下：
1
2
3
4
5
6%% 求微分方程组 clear all z = dsolve('Dx = y','Dy = x') z.x %查看x与t的函数 z.y %查看y与t的函数
结果如下：
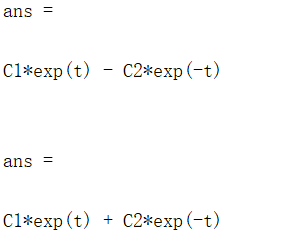
4. 求函数最小值和零点
示例如下：
1
2
3
4
5
6
7%% 求解一元函数的最小值和零点 format short clear all close all [x,fval]=fminbnd(@cos,1,5) y = cos(x)
结果如下：
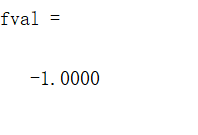  **限定自变量范围：**
1
2
3
4
5
6
7
8%% 限定自变量范围 clear all close all f = @(x)x.^2 - 6*x -9 [x,fval] = fminbnd(f,0,6,optimset('Display','iter')) %自变量在0到6之间的最小值，显示计算过程 y = f(x)
结果如下：
求多元函数最小值：
1
2
3
4
5
6
7%% 求多元函数最小值 clear all close all f = @(x) 2*(x(2)-x(1)^2)^2+(2-x(1))^2 [x,fval] = fminsearch(f,[-6.7 8]) %指定一个起始点 在-6.7和8附近开始查找最小值 y = f(x)
结果如下：
4. 求函数零点
示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
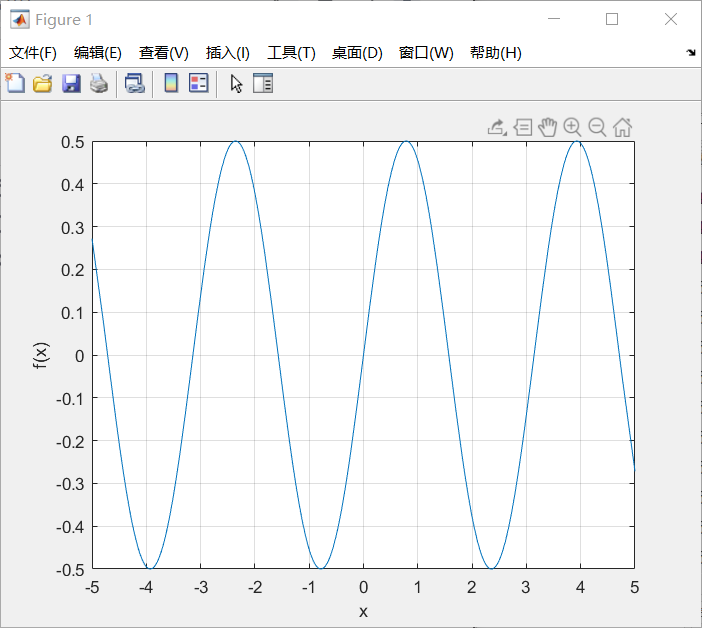
13%% 求一元函数的零点 clear all close all f = @(x)sin(x)*cos(x) figure fplot(f,[-5,5]) xlabel('x') ylabel('f(x)') grid on; x1 = fzero(f,[-4,-2]) x3 = fzero(f,-2) [x4,fval] = fzero(f,[-3,1])
结果如下：
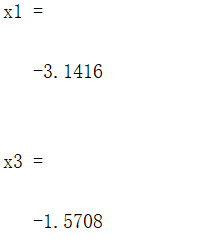
五、矩阵升级操作
矩阵排序：
1
2
3
4
5
6
7
8
9%% 矩阵排序 clear all clc A = [3 4 0; 6 85 9;4 5 10] B = sort(A) %每一列从小到大排序 C = sort(A,'descend') %降序 D = sort(A,2,'descend') %按照行排序
结果如下：
矩阵差分：
1
2
3
4
5
6
7
8
9%% 矩阵差分 clear all clc A = [3 4 0; 6 85 9;4 5 10] diff(A) diff(A,2) %在列上进行二阶差分 diff(A,1,1) %在列上进行一阶差分 diff(A,1,2) %在行上进行一阶差分
结果如下：
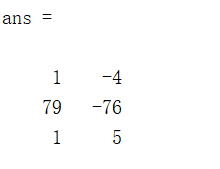
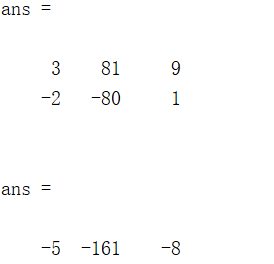
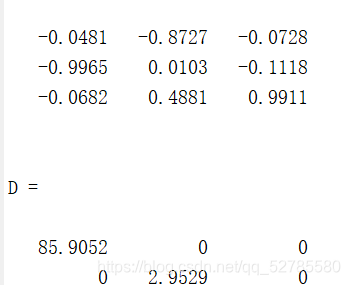
求特征值：
1
2
3
4
5
6
7%% 求矩阵的特征值 clear all clc A = [3 4 0; 6 85 9;4 5 10] E = eig(A) %求矩阵的全部特征值，是一个向量 [V,D] = eig(A) %V的每列是一个特征向量，D的对角线上的元素时特征值
结果如下：
 **求方程的根：**
1
2
3
4
5
6
7
8%% 求方程的根 clear all clc A = [3 4 0] Aa = compan(A) %求A的伴随矩阵 x1 = eig(Aa) %求特征值就是根 x2 = roots(A) %另一种方法
结果如下：
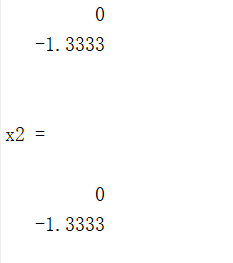
矩阵求秩：
1
2
3
4
5
6%% 求方程的秩 clear all clc A = [3 4 0] r = rank(A)
结果如下：
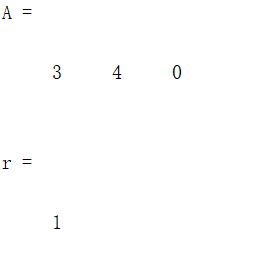
矩阵求范数：
1
2
3
4
5
6
7
8%% 求方程的范数 默认求2范数 clear all clc A = [3 4 0;2 56 34;1 2 2] n1 = norm(A,1) %求1范数 n2 = norm(A) %求2范数 n3 = norm(A,inf) %求无穷范数
结果如下：
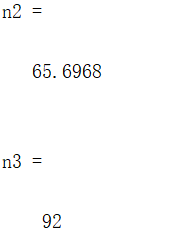
六、逻辑及流程控制
这一部分和以前的编译语言类似，但是MATLAB中所有流程执行完毕后需要在结尾加上end，不然程序无法判断结束。
1.if…else…end
示例如下：
1
2
3
4
5
6
7
8
9
10% if...else...end A = rand(1,10) B = A>0.5 if any(B) fprintf('Indices of values > %4.2f:n'); disp(find(B)) else disp('所有值都小于0.5') end
结果如下：
2. for…end
示例如下：
1
2
3
4
5
6
7
8
9
10%% for...end k = 5 hilbert = zeros(k,k) for m = 1:k for n = 1:k hilbert(m,n) = 1/(m+n - 1); end end
结果如下：
3. while…end
示例如下：
1
2
3
4
5
6
7
8
9%% while...end n = 1; nFactorial = 1; while nFactorial < 1e50 n = n+1; nFactorial = nFactorial * n; end n
结果如下：
3. switch…case…end
示例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14% switch...case...end m = input('请输入一个数字:') switch m case -1 disp('负一') case 0 disp('零') case 1 disp('正一') otherwise disp('其他') end
结果如下：
八、文件导入
1. mat格式
1
2
3
4
5%% mat格式 save data.mat x y1 y2 clear all load data.mat %加载文件
2. txt格式
1
2
3
4
5
6
7
8
9%% txt格式 M = importdata('myfile.txt'); S = M.data; %将文本中的数据单独拿出来 save 'data.txt' S -ascii T = load('data.txt'); isequal(S,T)
3. xls格式
1
2
3
4
5
6
7
8
9%% xls格式 xlswrite('data.xls',S) W = xlsread('data.xls'); isequal(S,W) xlswrite('data.xlsx',S) U = xlsread('data.xlsx'); isequal(S,T)
4. csv格式
1
2
3
4
5%% csv格式 csvwrite('data.csv',S) V = csvread('data.csv') isequal(S,V)
九、随机数的产生
1. 二项分布随机数
示例如下：
1
2
3
4
5
6
7%% 随机数的产生 %% 二项分布随机数 clear all r = binornd(6,0.8) R = binornd(6,0.8,4,5) %产生一个4*5的矩阵
结果如下：
2. 泊松分布随机数
示例如下：
1
2
3
4
5%% 泊松分布随机数 clear all r = poissrnd(6) %泊松分布 R = poissrnd(6,3,3) %产生一个3*3的矩阵
结果如下：
3. 均匀分布随机数
均匀性：
1
2
3
4
5
6
7%% 均匀分布随机数 % 连续型 clear all r = unifrnd(1,5) %均匀分布 1到5之间 R = unifrnd(1,5,3,3) %产生一个3*3的矩阵
结果如下：
离散型：
1
2
3
4
5% 离散型 clear all r = unidrnd(6) R = unidrnd(6,3,3)
结果如下：
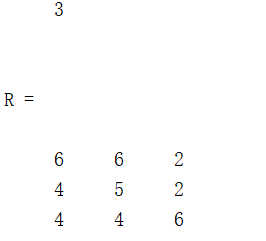
4. 正态分布
示例如下：
1
2
3
4
5
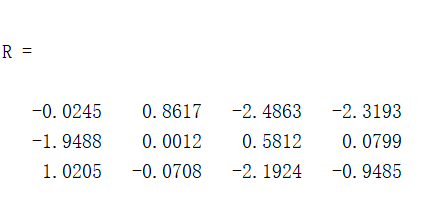
6%% 正态分布 clear all r = normrnd(0,1) R = normrnd(0,1,[3 4]) % 产生一个3*4的矩阵，均值为0，标准差为1
结果如下：
十、MATLAB绘图
MATLAB具有强大的绘图功能，可以绘制各种各样的图，这里为大家展示几种。
一元函数：
1
2
3
4
5
6
7
8
9
10
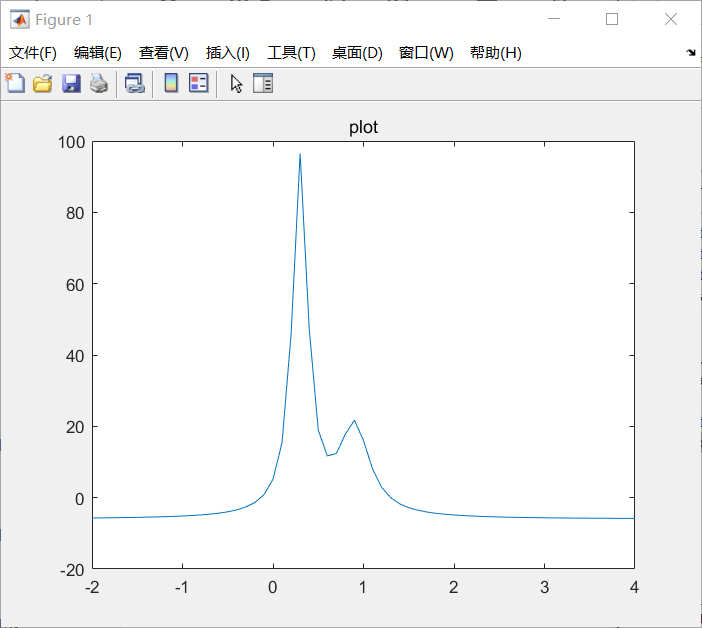
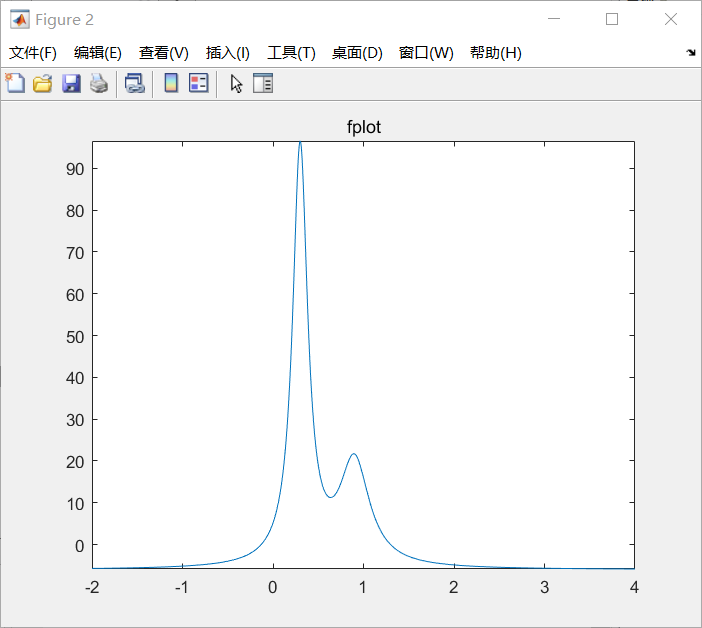
11%% MATLAB绘图 %% 一元函数 x = -2:0.1:4; figure; plot(x,humps(x)); title('plot'); figure; fplot(@humps,[-2,4]) %曲线更加光滑 title('fplot');
结果如下：
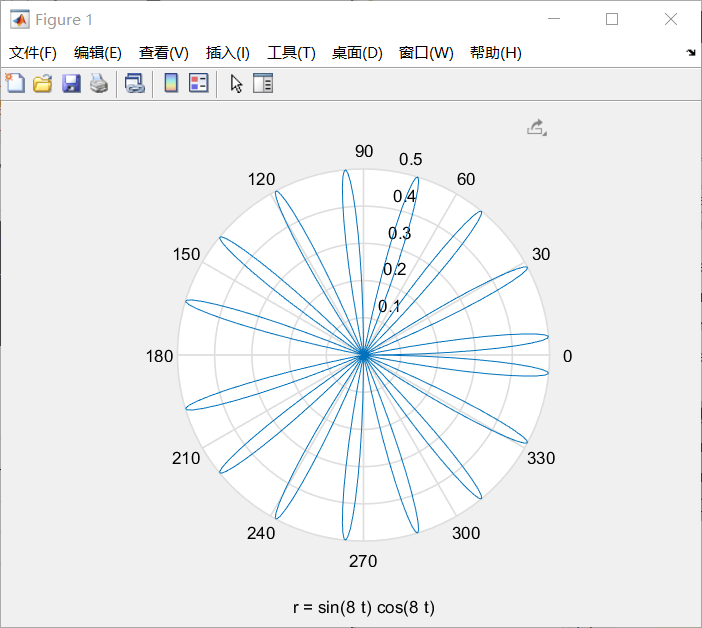
极坐标绘图：
1
2
3
4
5%% 极坐标绘图 clear all figure; ezpolar('sin(8*t).*cos(8*t)',[0,pi]);
结果如下：
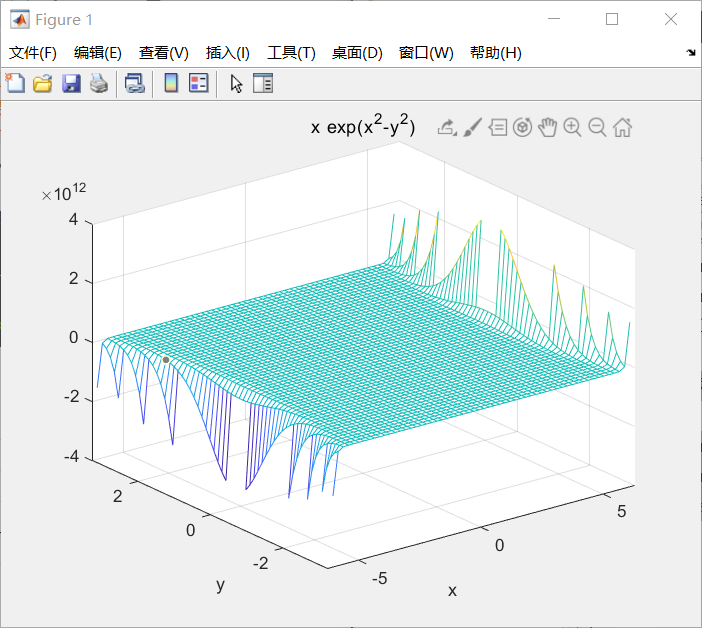
符号函数的三位网格图：
1
2
3
4
5
6%% 符号函数的三位网格图 clear all figure; ezmesh('x.*exp(x.^2-y.^2)');
结果如下：
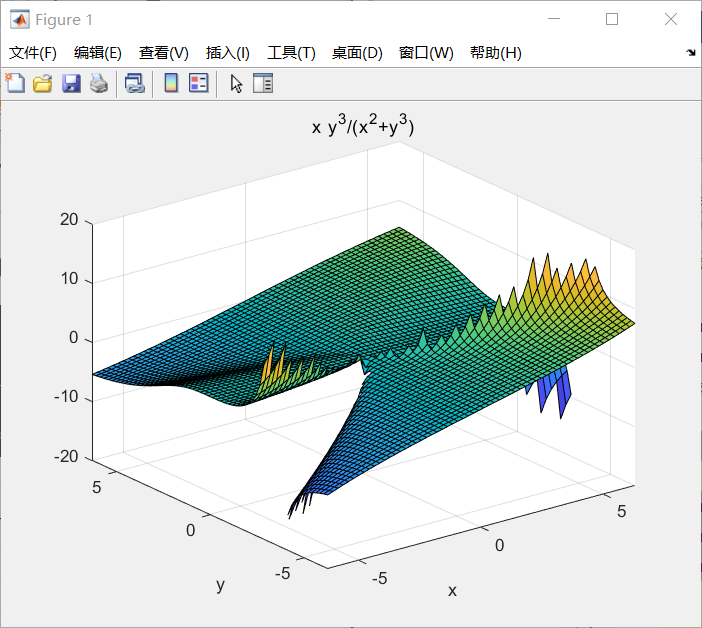
三维彩色曲面图：
1
2
3
4
5
6%% 三维彩色曲面图 clear all figure; ezsurf('x.*y.^3/(x.^2+y.^3)');
结果如下：
上述两种图形都可以加等值面或等值线，只需要在相应函数后加“c”即可。
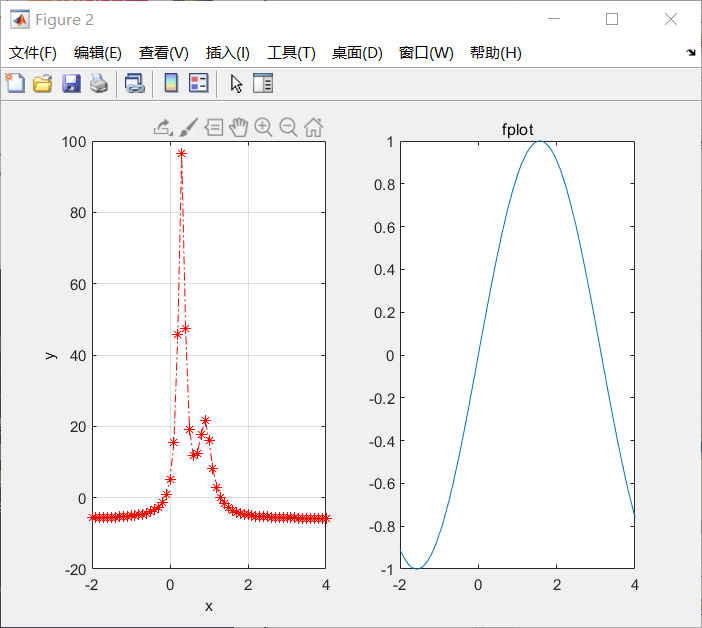
绘图更多操作：
1
2
3
4
5
6
7
8
9
10
11
12
13
14%% 一元函数 x = -2:0.1:4; figure; %显示绘图界面 subplot(1,2,1) %同时显示两个图 plot(x,humps(x),'r-.*'); %绘图 title('plot'); %题目 xlabel('x') %加横坐标标签x ylabel('y') %加纵坐标标签y grid on; %显示网格线 hold on; subplot(122) fplot(@sin,[-2,4]) %曲线更加光滑 title('fplot');
结果如下：
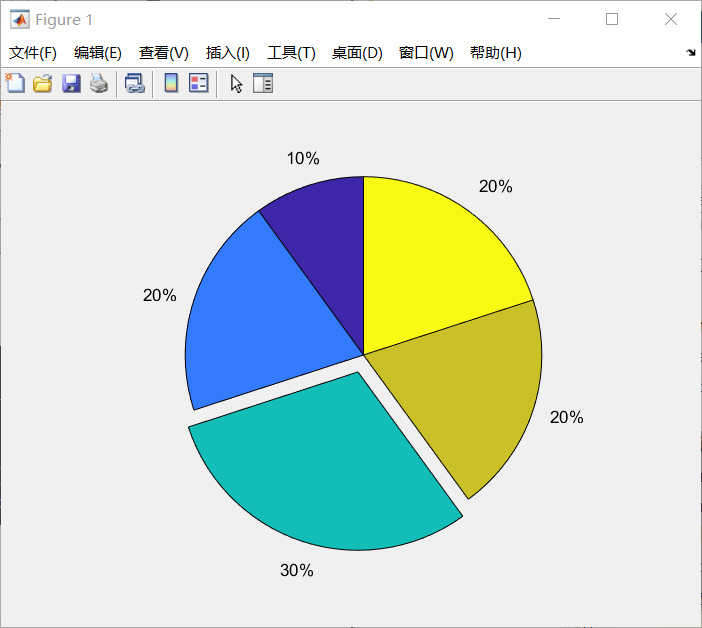
饼状图：
1
2
3
4
5
6
7%% 饼状图 clear all figure; y = [0.1 0.2 0.3 0.2 0.2]; explode=[0 0 1 0 0] %第三个突出 pie(y,explode);
结果如下：
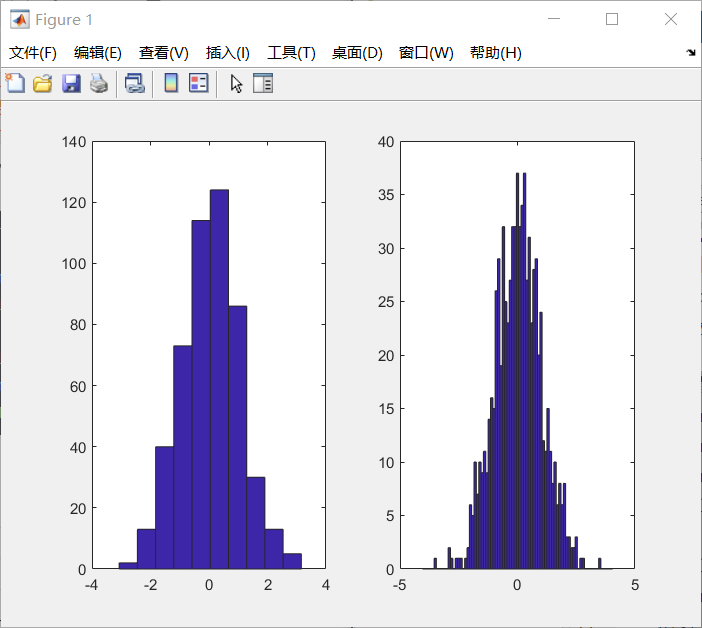
直方图：
1
2
3
4
5
6
7
8
9
10%% 直方图 clear all figure; x = randn(500,1) %标准正态分布 subplot(121) hist(x); %默认十个柱子 subplot(122); y = randn(800,1) hist(y,-4:0.1:4);
结果如下：
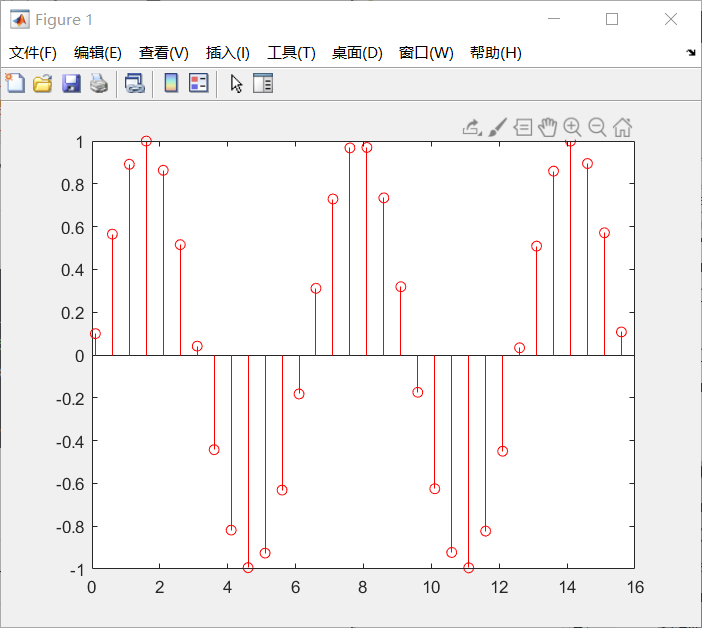
火柴杆图：
1
2
3
4
5
6
7%% 火柴杆图 clear all x = 0.1:0.5:5*pi y = sin(x) figure; stem(x,y,'r')
结果如下：
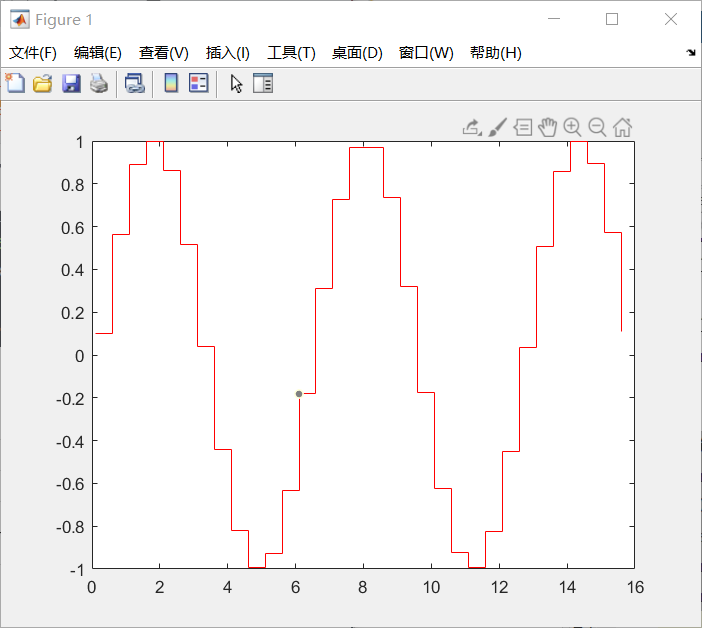
阶梯图：
1
2
3
4
5
6
7%% 阶梯图 clear all x = 0.1:0.5:5*pi y = sin(x) figure; stairs(x,y,'r')
结果如下：
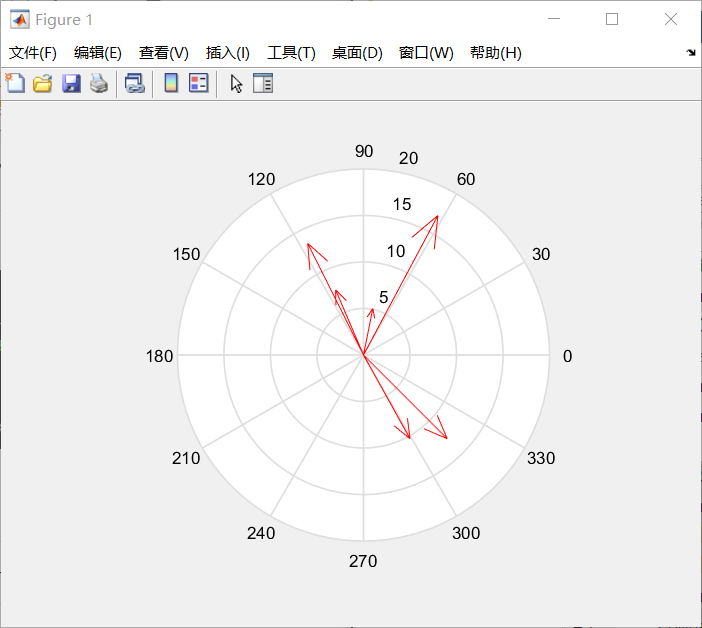
罗盘图：
1
2
3
4
5
6
7%% 罗盘图 clear all; x = [1 -3 5 -6 8 9]; y = [5 7 -9 12 15 -9]; figure; compass(x,y,'r')
结果如下：
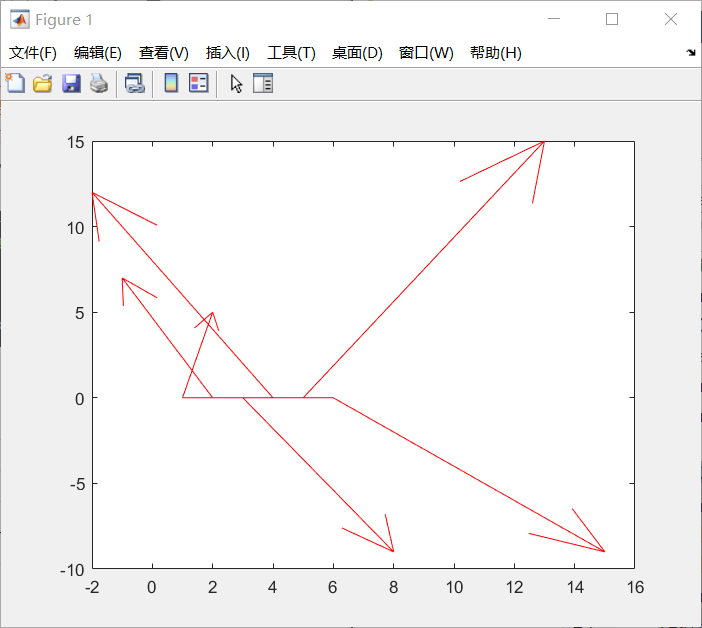
羽毛图：
1
2
3
4
5
6
7%% 羽毛图 clear all; x = [1 -3 5 -6 8 9]; y = [5 7 -9 12 15 -9]; figure; feather(x,y,'r')
结果如下：
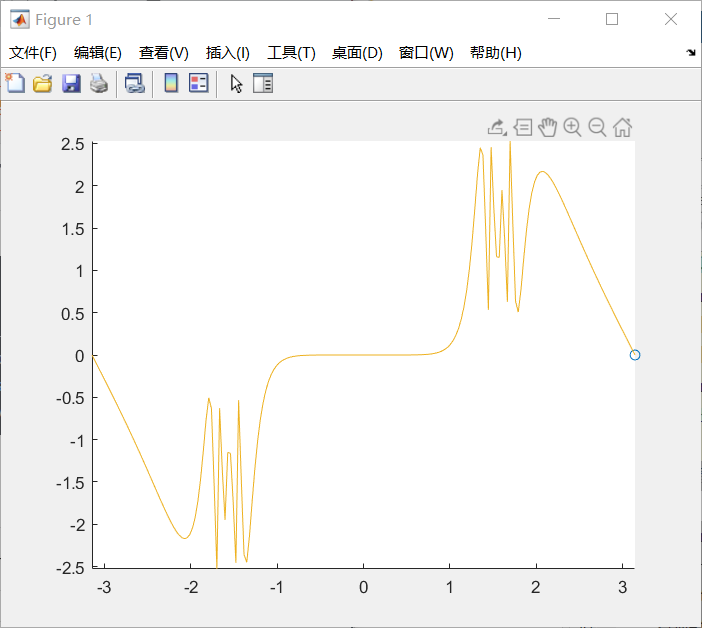
彗星图：
1
2
3
4
5
6
7%% 彗星图 clear all t = -pi:pi/100:pi; y = tan(sin(t))-sin(tan(t)); comet(t,y);
结果如下：
这篇MATLAB笔记写的太简陋了，美国也限制我们学校使用MATLAB，所以可能MATLAB也不会成为我日后使用的主力，还是好好学C++和python吧！
这篇文章就酱。
最后
以上就是疯狂夏天最近收集整理的关于MATLAB从入门到入土前言一、数据类型二、数据显示格式三、运算方法和求积分四、求解微分方程和函数最小值及零点五、矩阵升级操作六、逻辑及流程控制八、文件导入九、随机数的产生十、MATLAB绘图的全部内容，更多相关MATLAB从入门到入土前言一、数据类型二、数据显示格式三、运算方法和求积分四、求解微分方程和函数最小值及零点五、矩阵升级操作六、逻辑及流程控制八、文件导入九、随机数内容请搜索靠谱客的其他文章。
发表评论 取消回复