非相参累积和相参累积检测

在雷达回波检测中，在特殊情况下，才会根据单个脉冲来进行检测判决。通常，雷达会从每个目标接收几个到几百个成串脉冲，在做出判决之前，要先对脉冲串进行处理。对脉冲串进行处理的方法有5种：

1. 相参累积（Coherent Integration）；
2. 非相参累积（Nocoherent Integration）；
3. 二进制累积；
4. 累计检测；
5. 反馈累积器。

1 非相参累积

也叫“检波后累积”，或者“视频累积”（Video Integration），比检波前累积更容易完成，因为不需要保存回波的相位。只需要将脉冲的包络对准就可以相加。

非相参累积由于没有利用相位信息必然有损于信噪比。

设$X_{ij}$为输入脉冲矩阵的第$(i,j)$个元素，则这个输入脉冲矩阵的非相参累积为：

$$Y_i=\sqrt{\sum _{j=1}^N{\left|X_{ij}\right|}^2}$$

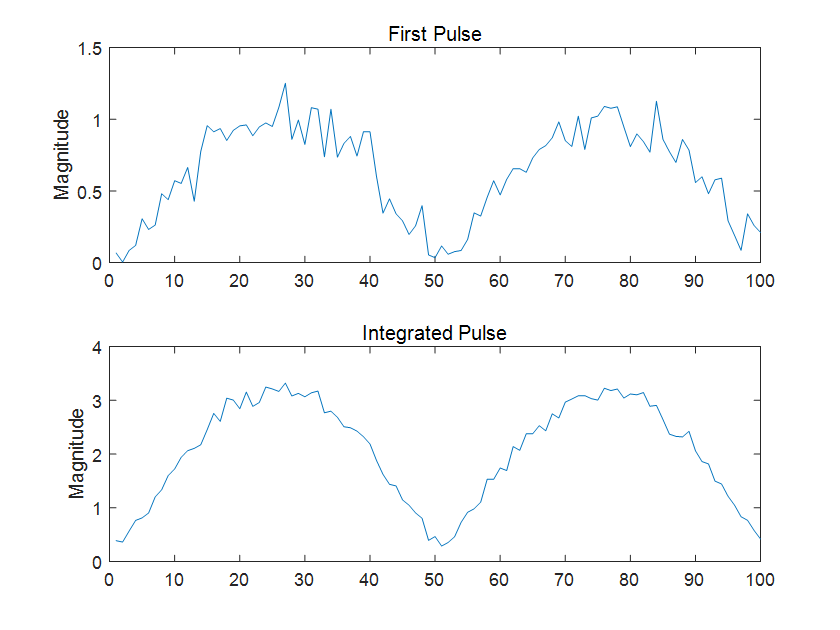
Matlab中的pulseint函数能够实现脉冲的非相参累积和相参累积，实现非相参累积的代码如下：

npulse = 10;
% 生成包含10个脉冲的脉冲矩阵，叠加噪声
x = repmat(sin(2*pi*(0:99)'/100),1,npulse) + 0.1*randn(100,npulse);
% 非相参累积
y = pulsint(x);

% 画图
subplot(2,1,1)
plot(abs(x(:,1)))
ylabel('Magnitude')
title('First Pulse')
subplot(2,1,2)
plot(abs(y))
ylabel('Magnitude')
title('Integrated Pulse')

2 相参累积

又叫“检波前累积”。

设$X_{ij}$为输入脉冲矩阵的第$(i,j)$个元素，则这个输入脉冲矩阵的相参累积为：

$$Y_i=\sum _{j=1}^N{X}_{ij}$$

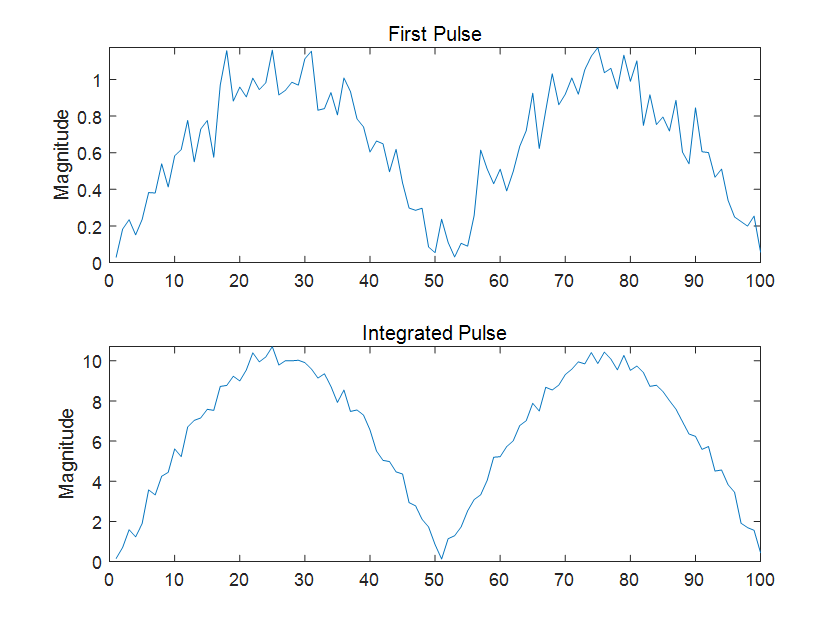
实现相参累积的代码如下：

npulse = 10;
% 生成包含10个脉冲的脉冲矩阵，叠加噪声
x = repmat(sin(2*pi*(0:99)'/100),1,npulse) + 0.1*randn(100,npulse);
% 相参累积，用'coherent'指定累积方式
y = pulsint(x,'coherent');

% 画图
subplot(2,1,1)
plot(abs(x(:,1)))
ylabel('Magnitude')
title('First Pulse')
subplot(2,1,2)
plot(abs(y))
ylabel('Magnitude')
title('Integrated Pulse')

最后

以上就是怕黑豌豆为你收集整理的雷达系统仿真——非相参累积和相参累积检测非相参累积和相参累积检测的全部内容，希望文章能够帮你解决雷达系统仿真——非相参累积和相参累积检测非相参累积和相参累积检测所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。