8.隐函数求导和相关变化率
8.1 隐函数求导
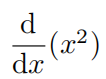
当对
x
x
x 稍作改变时,量
x
2
x^2
x2 会有多大变化
分母
d
x
dx
dx 告诉我们这是在关于
x
x
x 求导
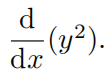
当对
x
x
x 稍作改变时,量
y
2
y^2
y2 会有多大变化
分母
d
x
dx
dx 告诉我们这是在关于
x
x
x 求导
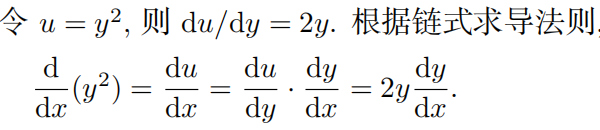
8.1.1 技巧和例子
例1:
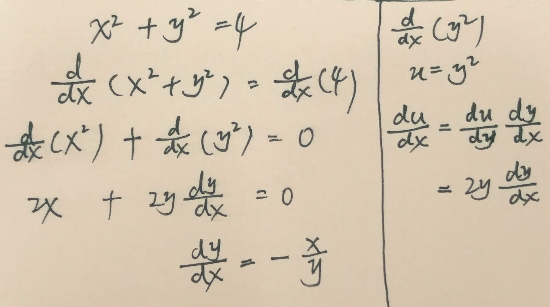
例2:
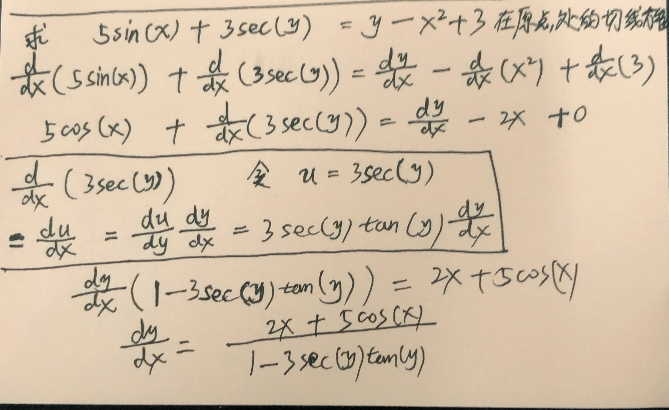
例3:

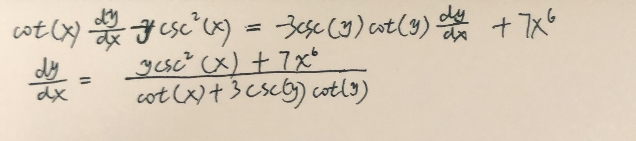
隐函数求导的技巧:


8.1.2 隐函数求二阶导
一阶导的平方: ( d y d x ) ( d y d x ) = ( d y d x ) 2 (frac{dy}{dx})(frac{dy}{dx})=(frac{dy}{dx})^2 (dxdy)(dxdy)=(dxdy)2
二阶导:
d
d
x
(
d
y
d
x
)
=
d
2
y
d
x
2
frac{d}{dx}(frac{dy}{dx})=frac{d^2y}{dx^2}
dxd(dxdy)=dx2d2y
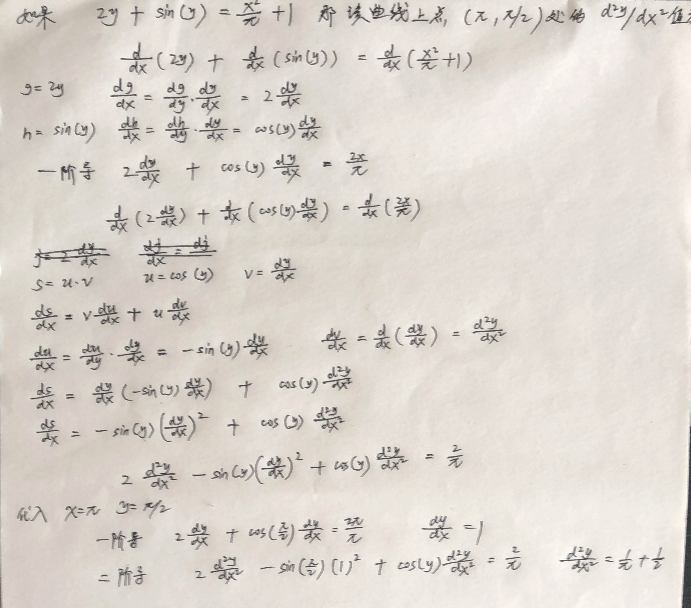
技巧:如果需要的只是特定点上的导数,可以在整理关于 d y d x = ( . . . ) frac{dy}{dx}=(...) dxdy=(...)的式子前,直接用数值替换(从而省去整理式子的时间)
8.2 相关变化率
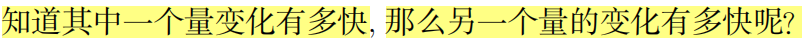


求解相关变化率问题的一般方法:

例子:

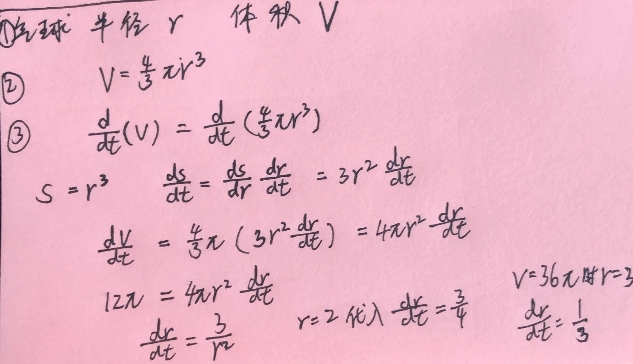
最后
以上就是曾经夕阳最近收集整理的关于隐函数求导和相关变化率8.隐函数求导和相关变化率的全部内容,更多相关隐函数求导和相关变化率8内容请搜索靠谱客的其他文章。








发表评论 取消回复