等距圆柱投影

1 理论部分

符号说明

1.1 Forward 投影

从球的表面投影到平面。

$$\begin{array}{rl}x& =R(\lambda -{\lambda }_0)cos{\varphi }_1\\ y& =R(\varphi -{\varphi }_0)\end{array}$$

1.2 Reverse 投影

从平面投影到球表面。
$$\begin{array}{rl}\lambda & =\frac{x}{Rcos{\varphi }_1}+{\lambda }_0\\ \varphi & =\frac{y}{R}+{\varphi }_0\end{array}$$

1.3 标准纬线

标准纬线是圆柱与球体相切或相割的纬线。

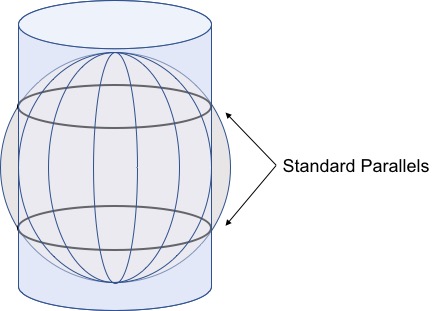
对于全景图片（视频）来说，标准纬线为赤道。此时$cos{\varphi }_1=1$。

1.4 极坐标转直角坐标

1.4.1 表示图

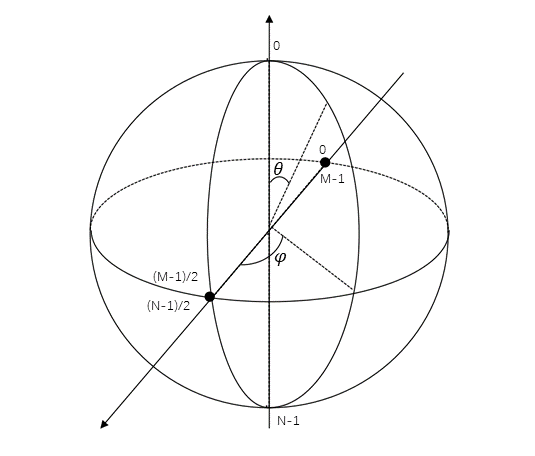
1.4.2 Python 代码

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d as p3d
import math
from PIL import Image

fig = plt.figure()
ax = p3d.Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(ax)

z = []
x = []
y = []
c = []
img = Image.open('000.png')
img_array = np.array(img, dtype=np.float) / 255.0
N, M, C = img_array.shape

r = (N / math.pi + M / (2 * math.pi)) / 2
for j in range(N):
    for i in range(M):
        theta = j / N * math.pi
        phi = (i - (M - 1) / 2) / M * 2 * math.pi
        x.append(r * math.sin(theta) * math.cos(phi))
        y.append(r * math.sin(theta) * math.sin(phi))
        z.append(r * math.cos(theta))
        c.append((img_array[j, i, 0], img_array[j, i, 1], img_array[j, i, 2]))

ax.scatter(x, y, z, c=c)
plt.show()

2 效果展示

2.1 原图

2.2 效果图

为展示方便，绘制在了球体外表面。

2.3 稀疏图

外表面。

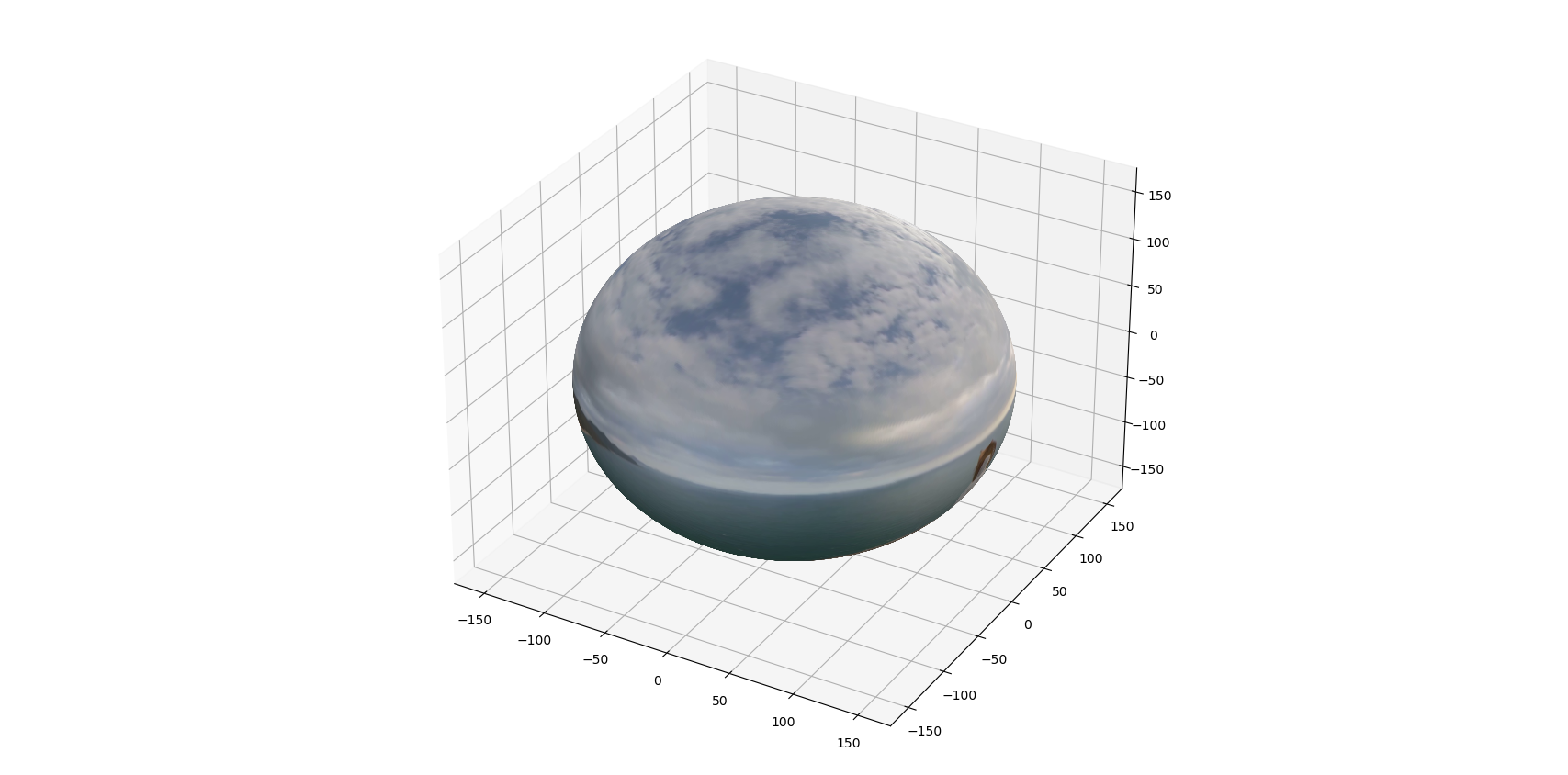
2.3 稀疏图

最后

以上就是心灵美哑铃为你收集整理的等距圆柱投影的全部内容，希望文章能够帮你解决等距圆柱投影所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。