【宇宙狗的危机】CSP模测T4

71 阅读 0 评论 47 点赞

我是靠谱客的博主现代戒指，最近开发中收集的这篇文章主要介绍【宇宙狗的危机】CSP模测T4，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目

题目描述
在瑞神大战宇宙射线中我们了解到了宇宙狗的厉害之处，虽然宇宙狗凶神恶煞，但是宇宙狗有一个很可爱的女朋友。
最近，他的女朋友得到了一些数，同时，她还很喜欢树，所以她打算把得到的数拼成一颗树。
这一天，她快拼完了，同时她和好友相约假期出去玩。贪吃的宇宙狗不小心把树的树枝都吃掉了。所以恐惧包围了宇宙狗，他现在要恢复整棵树，但是它只知道这棵树是一颗二叉搜索树，同时任意树边相连的两个节点的gcd(greatest common divisor)都超过1。
但是宇宙狗只会发射宇宙射线，他来请求你的帮助，问你能否帮他解决这个问题。
补充知识：
GCD：最大公约数，两个或多个整数共有约数中最大的一个，例如8和6的最大公约数是2。
一个简短的用辗转相除法求gcd的例子：
int gcd(int a,int b){return b == 0 ? a : gcd(b,a%b);}
输入描述
输入第一行一个t，表示数据组数。
对于每组数据，第一行输入一个n，表示数的个数
接下来一行有n个数 $a_i$ ，输入保证是升序的。
输出描述
每组数据输出一行，如果能够造出来满足题目描述的树，输出Yes，否则输出No。
无行末空格。
样例输入1
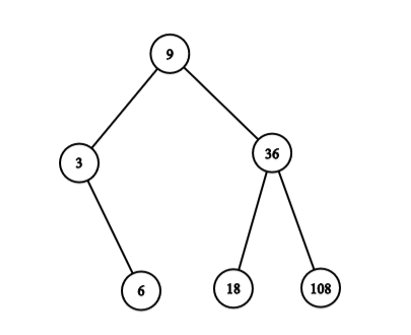
1 6 3 6 9 18 36 108
样例输出1
Yes
样例输入2
2 2 7 17 9 4 8 10 12 15 18 33 44 81
样例输出2
No Yes
样例解释
样例1可构造如下图

题目大意

本题给出若干组数据。对于每组数据，给出的数字升序排列，询问这些数字是否可以构成一棵二叉搜索树，并且任意一条数边相连的两个节点数字的最大公约数大于1。如果满足上述条件输出“Yes”，否则输出“No”。

解题思路

本题解决思路与动态规划的思想十分相似，总的来说就是用一个函数 sol (l, now, r) 来判断区间a[l+1]到a[r+1]这一区间内的以now做根节点now左侧为左子树，右侧为右子树是否可以满足要求。这里可以通过递归方法来实现，具体递归部分就是 sol (l, i, now) 和 sol (now, i, r) ,二者均返回true说明该区间满足条件。下面放出递归左子树的部分便于理解：

int flag = false;
if (l == now - 1) flag = true;
for (int i = l + 1; i < now; i++)
{
	if (getgcd[i][now] > 1)
	{
		if(sol(l, i, now)) flag = true;
	}
}
flag_l[l + 1][now + 1] = true;
ans_l[l + 1][now + 1] = flag;

本题中为了简化时间复杂度，可以提前记录下区间范围内是否满足条件，这里用两个数组 flag_l[705][705] 和 flag_r[705][705] 来表示区间 l+1~now+1 和区间 now+1~r+1 是否检查过，ans_l[705][705] 和 ans_r[705][705] 表示对应区间是否满足条件。递归过程中如果发现某段区间已经检查过，可以直接引用结果，免去重复计算过程。
本次题目的解答我也是参照了其他同学的博客，这里附上链接：解题思路参考

具体代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<iomanip>
#include <map>
#define ll long long
#define MAXN 105 
using namespace std;

int a[705];
int getgcd[705][705];
bool flag_l[705][705];
bool flag_r[705][705];
bool ans_l[705][705];
bool ans_r[705][705];
int t,n;

int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

bool sol(int l, int now, int r)
{
	if (flag_l[l + 1][now + 1] && flag_r[now + 1][r + 1])
	{
		return (ans_l[l + 1][now + 1] && ans_r[now+1][r + 1]);
	}
	if (l >= now - 1 && r <= now + 1)
	{
		return true;
	}
	if(!flag_l[l + 1][now + 1])
	{
		int flag = false;
		if (l == now - 1) flag = true;
		for (int i = l + 1; i < now; i++)
		{
			if (getgcd[i][now] > 1)
			{
				if(sol(l, i, now)) flag = true;
			}
		}
		flag_l[l + 1][now + 1] = true;
		ans_l[l + 1][now + 1] = flag;
	}
	if(!flag_r[now + 1][r + 1])
	{
		int flag = false;
		if (now == r - 1) flag = true;
		for (int i = now + 1; i < r; i++)
		{
			if (getgcd[now][i] > 1)
			{
				if(sol(now, i, r)) flag = true;
			}
		}
		flag_r[now + 1][r + 1] = true;
		ans_r[now + 1][r + 1] = flag;
	}
	return (ans_l[l + 1][now + 1] && ans_r[now + 1][r + 1]);
}

int main()
{
	cin >> t;
	while(t--)
	{
		memset(flag_l,0,sizeof(flag_l));
		memset(flag_r,0,sizeof(flag_r));
		memset(ans_l,0,sizeof(ans_l));
		memset(ans_r,0,sizeof(ans_r));
		cin >> n;
		for(int i = 0; i < n; i++) cin >> a[i];
		for(int i = 0; i < n; i++)
		{
			for(int j = i; j < n; j++)
			{
				getgcd[i][j] = gcd(a[i],a[j]);
				getgcd[j][i] = getgcd[i][j];
			}
		}
		int ans = 0;
		for(int i = 0; i < n; i++)
		{
			if(ans) break;
			if(sol(-1,i,n)) ans = 1;
		}
		if(ans) cout << "Yes" << endl;
		else cout << "No" << endl;
	}
    return 0;
}