一、PG回顾

1、对于离散动作，策略搜索使用神经网络来参数化随机策略中的动作概率，网络的输入是智能体的当前状态，网络输出为当前所有动作的概率，该网络是一种分类网络。网络训练使用数据为一个episode数据（s,a,r）. 参考https://blog.csdn.net/weixin_40493501/article/details/110384894

2、对于连续性动作来说，一般使用随机高斯策略，网络的输入是智能体当前状态，网络的输出的高斯策略的均值和标准差，网络是一个拟合网络。

无论是连续动作还是离散动作，在使用PG时，必须先弄清下面公式【主要推导上一个文章已给出】，离散动作和连续动作最大的不同就在于。

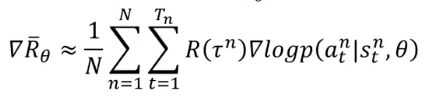
   在离散动作的网络设计中，输入是状态，输出可以看做是每个动作的概率，与动作标签进行对比，尽量使动作概率的输出接近标签。

   在连续动作中，将看成是动作的分布，例如高斯分布

二、连续动作PG算法网络

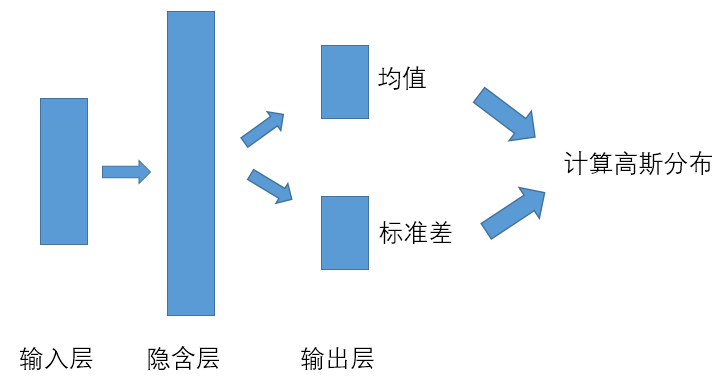
输入层为状态，连续动作空间的输出层不再是动作，二是动作描述的一种分布参数，利用输出的参数可以得到动作的分布，可以根据分布来选择动作。

【需要补充具体的计算过程】

三、代码实现

import tensorflow as tf
import numpy as np
import gym
import matplotlib.pyplot as plt
RENDER = False

'''
连续动作
使用的是高斯策略，用神经网络参数化高斯分布的均值和方差

状态空间为 2
动作空间为 1   其取值范围在[-2,2]之间
注意其误差的构建


'''

#利用当前策略进行采样，产生数据
class Sample():
    def __init__(self,env, policy_net):
        self.env = env
        self.policy_net=policy_net
        self.gamma = 0.95
    def sample_episodes(self, num_episodes):
        #产生num_episodes条轨迹
        batch_obs=[]
        batch_actions=[]
        batch_rs =[]
        for i in range(num_episodes):
            observation = self.env.reset()
            #将一个episode的回报存储起来
            reward_episode = []
            while True:
                # if RENDER:self.env.render()
                #根据策略网络产生一个动作
                state = np.reshape(observation,[1,3])
                action = self.policy_net.choose_action(state)
                observation_, reward, done, info = self.env.step(action)
                # print("observation",observation_)
                batch_obs.append(np.reshape(observation,[1,3])[0,:])
                # print('observation', np.reshape(observation,[1,3])[0,:])
                batch_actions.append(action)
                reward_episode.append((reward+8)/8)
                #一个episode结束
                if done:
                    #处理回报函数
                    reward_sum = 0
                    discouted_sum_reward = np.zeros_like(reward_episode)
                    for t in reversed(range(0, len(reward_episode))):
                        reward_sum = reward_sum*self.gamma + reward_episode[t]
                        discouted_sum_reward[t] = reward_sum
                    #归一化处理
                    discouted_sum_reward -= np.mean(discouted_sum_reward)
                    discouted_sum_reward/= np.std(discouted_sum_reward)
                    #将归一化的数据存储到批回报中
                    for t in range(len(reward_episode)):
                        batch_rs.append(discouted_sum_reward[t])
                        # print(discouted_sum_reward[t])
                    break
                #智能体往前推进一步
                observation = observation_
        #reshape 观测和回报
        batch_obs = np.reshape(batch_obs, [len(batch_obs), self.policy_net.n_features])
        batch_actions = np.reshape(batch_actions,[len(batch_actions),1])
        batch_rs = np.reshape(batch_rs,[len(batch_rs),1])
        return batch_obs, batch_actions,batch_rs
#定义策略网络
class Policy_Net():
    def __init__(self, env, action_bound, lr = 0.0001, model_file=None):
        self.learning_rate = lr
        #输入特征的维数
        self.n_features = env.observation_space.shape[0]
        #输出动作空间的维数
        self.n_actions = 1     # 注意动作维度只有一个
        #1.1 输入层
        self.obs = tf.placeholder(tf.float32, shape=[None, self.n_features])
        #1.2.第一层隐含层
        self.f1 = tf.layers.dense(inputs=self.obs, units=200, activation=tf.nn.relu, kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.1),
                             bias_initializer=tf.constant_initializer(0.1))
        #1.3 第二层，均值，需要注意的是激活函数为tanh，使得输出在-1~+1
        mu = tf.layers.dense(inputs=self.f1, units=self.n_actions, activation=tf.nn.tanh, kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.1),
                                       bias_initializer=tf.constant_initializer(0.1))
        #1.3 第二层，标准差
        sigma = tf.layers.dense(inputs=self.f1, units=self.n_actions, activation=tf.nn.softplus, kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.1),
                                       bias_initializer=tf.constant_initializer(0.1))
        #均值乘以2，使得均值取值范围在(-2,2)
        self.mu = 2*mu
        self.sigma =sigma
        # 定义带参数的正态分布
        self.normal_dist = tf.contrib.distributions.Normal(self.mu, self.sigma)
        #根据正态分布采样一个动作
        self.action = tf.clip_by_value(self.normal_dist.sample(1), action_bound[0],action_bound[1])
        #1.5 当前动作
        self.current_act = tf.placeholder(tf.float32, [None,1])
        self.current_reward = tf.placeholder(tf.float32, [None,1])
        #TODO 2. 构建损失函数
        log_prob = self.normal_dist.log_prob(self.current_act)
        self.loss = tf.reduce_mean(log_prob*self.current_reward+0.01*self.normal_dist.entropy())


        #3. 定义一个优化器
        self.train_op = tf.train.AdamOptimizer(self.learning_rate).minimize(-self.loss)
        #4. tf工程
        self.sess = tf.Session()
        #5. 初始化图中的变量
        self.sess.run(tf.global_variables_initializer())
        #6.定义保存和恢复模型
        self.saver = tf.train.Saver()
        if model_file is not None:
            self.restore_model(model_file)
    #依概率选择动作
    def choose_action(self, state):
        action = self.sess.run(self.action, {self.obs:state})
        return action[0]
    #定义训练
    def train_step(self, state_batch, label_batch, reward_batch):
        loss, _ =self.sess.run([self.loss, self.train_op], feed_dict={self.obs:state_batch, self.current_act:label_batch, self.current_reward:reward_batch})
        return loss
    #定义存储模型函数
    def save_model(self, model_path):
        self.saver.save(self.sess, model_path)
    #定义恢复模型函数
    def restore_model(self, model_path):
        self.saver.restore(self.sess, model_path)

def policy_train(env, brain, training_num):
    reward_sum = 0
    reward_sum_line = []
    training_time = []
    brain = brain
    env = env
    for i in range(training_num):
        temp = 0
        sampler = Sample(env, brain)
        # 采样1个episode
        train_obs, train_actions, train_rs = sampler.sample_episodes(1)
        brain.train_step(train_obs, train_actions, train_rs)
        if i == 0:
            reward_sum = policy_test(env, brain,RENDER,1)[0]
        else:
            reward_sum = 0.95 * reward_sum + 0.05 * policy_test(env, brain,RENDER,1)[0]
        # print(policy_test(env, brain))
        reward_sum_line.append(reward_sum)
        training_time.append(i)
        print("training episodes is %d,trained reward_sum is %f" % (i, reward_sum))
        if reward_sum > -200:
            break
    brain.save_model('./Pendulum_models/current_bset_pg_pendulum')
    plt.figure(1)
    plt.plot(training_time, reward_sum_line)
    plt.xlabel("training number")
    plt.ylabel("score")
    # plt.show()

def policy_test(env, policy,RENDER,test_number):
    test_reward = []
    for i in range(test_number):
        observation = env.reset()
        reward_sum = 0
        # 将一个episode的回报存储起来
        while True:
            if RENDER:
                env.render()
            # 根据策略网络产生一个动作
            state = np.reshape(observation, [1, 3])
            action = policy.choose_action(state)
            observation_, reward, done, info = env.step(action)
            reward_sum+=reward
            if done:
                break
            observation = observation_
        test_reward.append(reward_sum)

    return test_reward


    return reward_sum
if __name__=='__main__':
    #构建单摆类
    env_name = 'Pendulum-v0'
    env = gym.make(env_name)
    env.unwrapped
    env.seed(1)
    #定义力矩取值区间
    action_bound = [-env.action_space.high, env.action_space.high]
    #实例化一个策略网络
    brain = Policy_Net(env,action_bound)
    training_num = 200
    #训练策略网络
    policy_train(env, brain, training_num)
    #测试训练好的策略网络
    test_reward_sum = policy_test(env, brain, False, 20)

    plt.figure(2)
    plt.title("Test")
    plt.plot(test_reward_sum)
    plt.xlabel("Testing number")
    plt.ylabel("score")
    plt.show()

    plt.show()

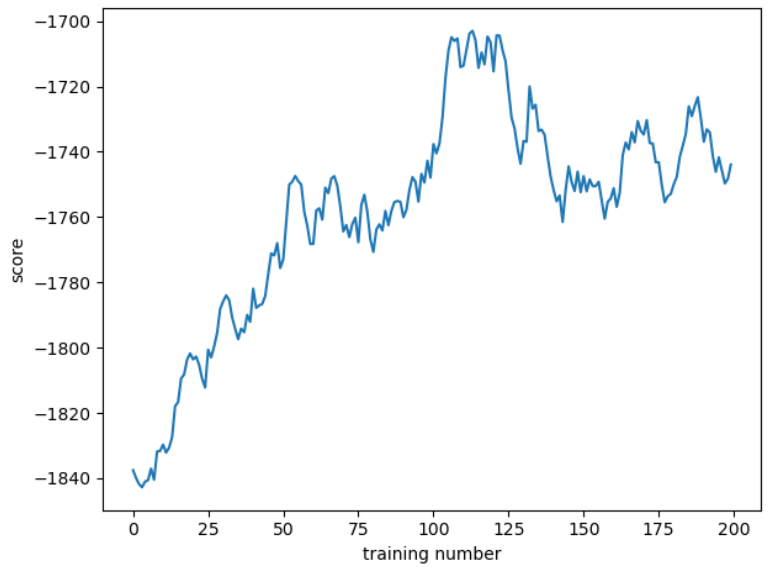
四、训练结果

一共训练200个episodes,训练完成后在进行测试20个episode（一个episode即为一条轨迹）

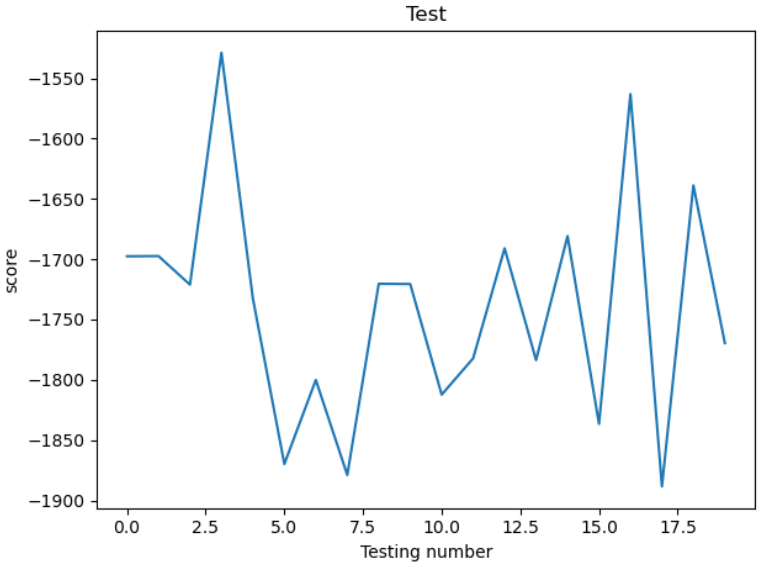
测试结果：

问题：

1、从训练的回报函数来看，网络并没有收敛，并且不是训练次数的问题，测试的结果波动较大，算法没有收敛是算法本身的缺陷还是实现过程出错？

2、从实验画面显示来看，倒立摆没有立起来，如何在不改变算法的前提下来改进训练效果，即如何调节PG算法收敛

继续学习中。。。。。。

最后

以上就是失眠绿草为你收集整理的02 强化学习——策略梯度法(PG)（连续动作）一、PG回顾二、连续动作PG算法网络三、代码实现四、训练结果的全部内容，希望文章能够帮你解决02 强化学习——策略梯度法(PG)（连续动作）一、PG回顾二、连续动作PG算法网络三、代码实现四、训练结果所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。