代码详见后面
实验三 树和二叉树
一、实验目的
1.使学生熟练掌握二叉树的逻辑结构和存储结构(重点)。
2.熟练掌握二叉树的各种遍历算法(难点)。
二、实验原理及说明
1. 前序遍历算法思想:
(1)访问根结点;
(2)前序遍历左子树;
(3)前序遍历右子树
2. 中序遍历算法思想:
(1)中序遍历左子树;
(2)访问根结点;
(3)中序遍历右子树。
3. 后序遍历算法思想:
(1)后序遍历左子树;
(2)后序遍历右子树;
(3)访问根结点。
4. 二叉树层次遍历算法思想:
本算法要采用一个队列q,先将二叉树根结点入队列,然后退队列,输出该结点;若它有左子树,便将左子树根结点入队列;若它有右子树,便将右子树根结点入队列,直到队列空为止。因为队列的特点是先进先出,从而达到按层次顺序遍历二叉树的目的。
三、实验内容
(一)问题描述
建立一棵二叉树,试编程实现二叉树的如下基本操作:
1. 按先序序列构造一棵二叉链表表示的二叉树T;
2. 对这棵二叉树进行遍历:先序、中序、后序以及层次遍历,分别输出结点的遍历序列;
3. 求二叉树的深度/结点数目/叶结点数目;
4. 将二叉树每个结点的左右子树交换位置。(选做)
(二)基本要求
从键盘接受输入(先序),以二叉链表作为存储结构,建立二叉树(以先序来建立),
四、实验安全事项
1.实验课中,保持实验室环境卫生。
2.实验完成后,应将仪器、工具及实验场地等进行清理、归还,经实验教师或实验技术人员同意后,方可离开实验室
3.实验室内禁止存放易燃易爆品及各类其它个人生活用品。禁止使用非实验用电器(如电加热器、电暖壶等)设备。
五、实验提交方式
□ 实验报告 □ 现场打分 √ 线上平台提交 □ 其它( )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126#include<iostream> using namespace std; //二叉树的二叉链表存储结构 typedef struct BiTNode{ char data; struct BiTNode* lchild, * rchild; }BiTNode, * BiTree; //先序建立二叉树 void CreateBiTree(BiTree& T){ char ch; cin>>ch; if (ch == '#') { T = NULL; } else { T = new BiTNode; T->data = ch; CreateBiTree(T->lchild); CreateBiTree(T->rchild); } } //先序遍历复制二叉树 void Copy(BiTree T, BiTree& NewT){ //空树 ,递归结束 if (T == NULL){ NewT = NULL; return ; } else{ NewT = new BiTNode; NewT->data = T->data; //复制 Copy(T->lchild, NewT->lchild); //递归复制左子树 Copy(T->rchild, NewT->rchild); //递归复制右子树 } } // 计算二叉树的深度 // 二叉树的深度为左右子树深度的较大者加1。 int Depth(BiTree T) { int m, n; if (T == NULL){ return 0; } else{ m = Depth(T->lchild); n = Depth(T->rchild); if (m > n) return (m + 1); else return (n + 1); } } //计算二叉树结点的个数 //二叉树的结点数为:左子树的结点数+右子树的结点数+1 int NodeCount(BiTree T){ if (T == NULL){ return 0; } else{ return NodeCount(T->lchild) + NodeCount(T->rchild) + 1; } } //先序遍历输出 void PreOrderTraverse(BiTree T) { if (T){ cout << T->data; PreOrderTraverse(T->lchild); PreOrderTraverse(T->rchild); } } //中序遍历输出 void InOrderTraverse(BiTree T) { if (T){ InOrderTraverse(T->lchild); cout << T->data; InOrderTraverse(T->rchild); } } //后序遍历输出 void PostOrderTraverse(BiTree T) { if (T){ PostOrderTraverse(T->lchild); PostOrderTraverse(T->rchild); cout << T->data; } } int main(){ BiTree T; int depth, node; cout<<"请输入要建立的二叉树(先序)用。#表示空树:"; CreateBiTree(T); depth = Depth(T); cout << "树的深度为:" << depth; cout << endl; node = NodeCount(T); cout << "树的节点个数为:" << node; cout << endl; //遍历a b c # # d e # # f # # g # # cout << "先序遍历:" ; PreOrderTraverse(T); cout << endl; cout << "中序遍历:"; InOrderTraverse(T); cout << endl; cout << "后序遍历:" ; PostOrderTraverse(T); cout << endl; }
运行代码:
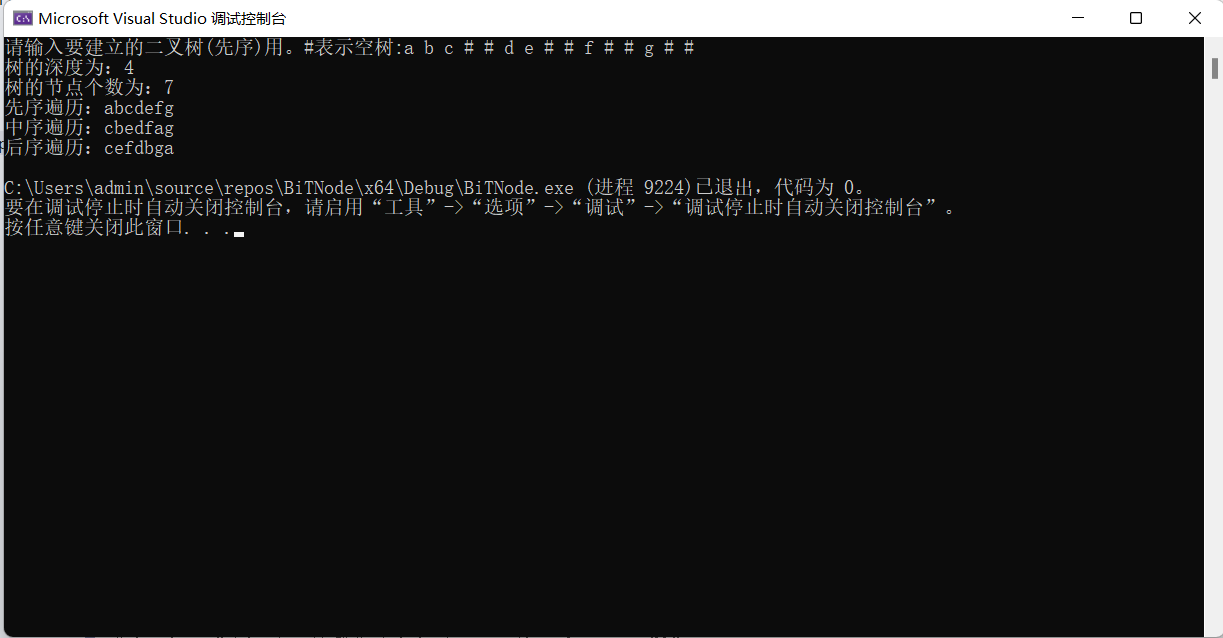
最后
以上就是感性歌曲最近收集整理的关于第五期 C/C++数据结构 二叉树的遍历以及结点数、深度的全部内容,更多相关第五期内容请搜索靠谱客的其他文章。








发表评论 取消回复