两点间距离、点到直线距离、点到线段距离、线段到线段距离

103 阅读 0 评论 68 点赞

我是靠谱客的博主欣喜面包，最近开发中收集的这篇文章主要介绍两点间距离、点到直线距离、点到线段距离、线段到线段距离，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

两点之间的距离

直接运用两点间距离公式 (x2-x1)^ 2+(y2-y1)^ 2开根号

//两点间距离
double getDistancePP(Point a,Point b)
{
//这个代码是部分代码,有些逻辑没有展现完全,大家往下看!
    Point c(b.x-a.x,b.y-a.y);//返回一个新的点
    return  c.abs();//取模
}

点到直线距离

通常给出3个点,其中两个点构成一条直线,求另外一个点到直线的距离,我们将点与点的关系转换为向量之间关系进而利用向量知识求出点到直线距离!

点到直线距离,我们可以利用外积的取模公式的几何意义,|axb|=|a|x|b|sinθ=所围成平行四边形面积,先求出向量a✖向量b的模,然后除以平行四边形底边边长|a|,最后用平行四边形面积除以底边边长就是高,也就是点到直线距离!

图解

在这里插入图片描述
不明白外积模的几何意义点击下方超链接
外积知识点大全

实现代码

//点到直线距离(利用外积平行四边形)
double getDistancePL(Point a,Point b,Point c)
{
    Vector ab(b.x-a.x,b.y-a.y);
    Vector ac(c.x-a.x,c.y-a.y);

    return cross(ab,ac)/ab.abs();//cross函数求两个向量的外积模,abs函数求向量模
}

点到线段距离

点到线段距离有一点复杂,因为线段不像直线那样可以无限延申,线段有端点,这就导致了点到线段距离可以分为3种情况!

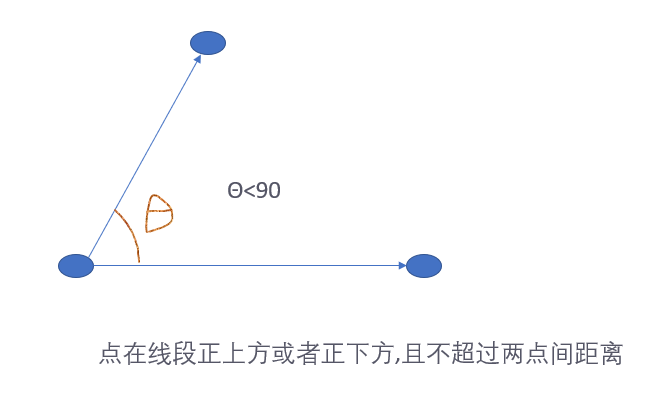
第一种:点到线段距离等于点到直线的距离
图示

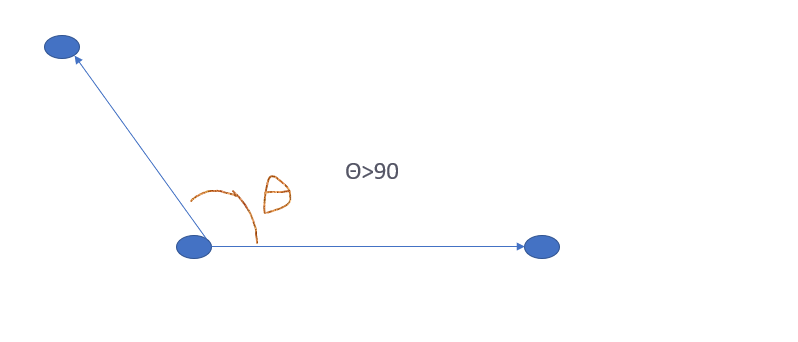
第二种:点到线段距离等于点到左端点的距离
图示

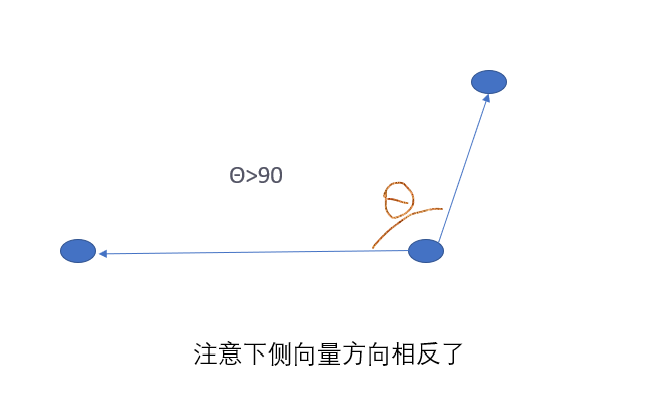
第三种:点到线段等于点到右端点的距离
图示

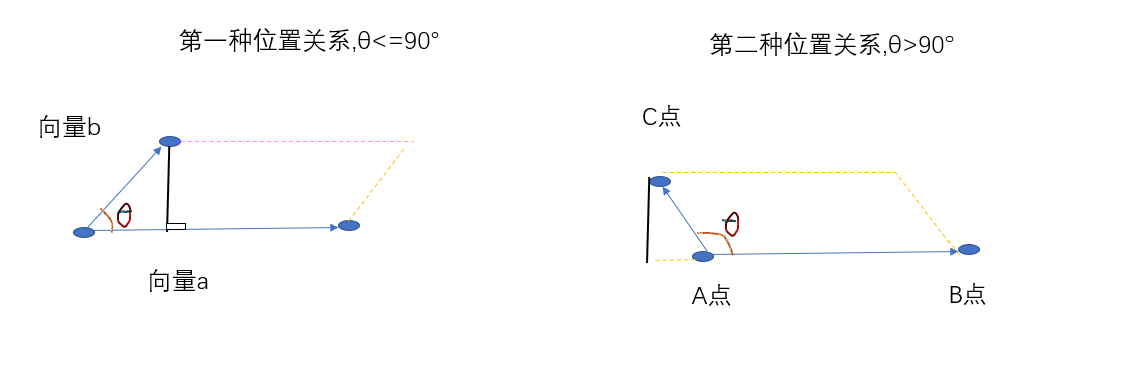
如何判断θ大小呢?

我们利用内积大小判断 a·b=|a|x|b|cosθ
如果a·b>0则θ在0~90°之间
如果a·b<0则θ在90°~180°之间

实现代码

//点到线段距离
double getDistancePS(Point a,Point b,Point c)
{
    //定义4个向量
    Vector ab(b.x-a.x,b.y-a.y);
    Vector ba(a.x-b.x,a.y-b.y);
    Vector ac(c.x-a.x,c.y-a.y);
    Vector bc(c.x-b.x,c.y-b.y);
    //dot函数用于求内积
    if(dot(ab,ac)<0.0) return getDistancePP(a,c);//到左端点距离
    if(dot(ba,bc)<0.0) return getDistancePP(b,c);//到右端点距离

    return getDistancePL(a,b,c);//点到直线距离
}

线段到线段距离

有了点到线段距离,求解线段到线段距离就容易多了!

首先、两个线段4个端点,我们分别用其中一个线段的一个端点,求出到另外一个线段的距离,在求出另一个端点到线段的距离,在更换线段,依次类推,我们求出4个不同的点到线段的距离,然后取最小值即可!

在代码中有一点我们暂时不考虑,就是两个线段相交的时候,那么他们的距离应该为0!

放在下一节学完两条线段相交的判定后直接添加一个if语句即可!

实现代码

//线段到线段的距离
double getDistanceSS(Point a,Point b,Point c,Point d)
{
    //从4个点到2线段距离中取最小
    return min(min(getDistancePS(c,d,a),getDistancePS(c,d,b)),min(getDistancePS(a,b,c),getDistancePS(a,b,d)));
}

完整代码

#include <bits/stdc++.h>

using namespace std;

class Point
{

public:
    double x,y;

    Point(double x=0,double y=0):x(x),y(y) {}

    //向量加法
    Point operator+(Point p)
    {
        return Point(x+p.x,y+p.y);
    }
    //向量减法
    Point operator-(Point p)
    {
        return Point(x-p.x,y+p.y);
    }
    //向量伸缩
    Point operator*(double a)
    {
        return Point(x*a,y*a);
    }
    Point operator/(double a)
    {
        return Point(x/a,y/a);
    }
    //向量大小
    double abs()
    {
        return sqrt(norm());
    }
    //向量范数
    double norm()
    {
        return x*x+y*y;
    }

    bool operator<(const Point &p) const
    {
        return x!=p.x?x<p.x:y<p.y;
    }

    bool operator==(const Point &p)const
    {
        return x-p.x<1e-10&&y-p.y<1e-10;
    }

};

typedef Point Vector;

//向量内积
double dot(Vector a,Vector b)
{
    return a.x*b.x+a.y*b.y;
}

//向量外积
double cross(Vector a,Vector b)
{
    return abs(a.x*b.y-a.y*b.x);
}

//正交
bool isOrthogonal(Vector a,Vector b)
{
    return a.x*b.x+a.y*b.y==0;
}
//平行
bool isParallel(Vector a,Vector b)
{
    return a.x*b.y-a.y*b.x==0;
}

//投影
Point project(Point a,Point b,Point c)
{
    Vector ab(b.x-a.x,b.y-a.y);
    Vector ac(c.x-a.x,c.y-a.y);
    double  r=dot(ab,ac)/ab.norm();//比例
    Vector h(ab*r);
    return Point(a.x+h.x,a.y+h.y);
}

//映象

Point reflect(Point a,Point b,Point c)
{
    //c到ab的投影点
    Point r=project(a,b,c);
    Vector cr(r.x-c.x,r.y-c.y);
    //cr扩大二倍
    Vector cr_2=cr*2;//上面重载过*
    //向量加法
    return Point(c.x+cr_2.x,c.y+cr_2.y);
}

//两点间距离
double getDistancePP(Point a,Point b)
{
    Point c(b.x-a.x,b.y-a.y);
    return  c.abs();
}

//点到直线距离(利用外积平行四边形)
double getDistancePL(Point a,Point b,Point c)
{
    Vector ab(b.x-a.x,b.y-a.y);
    Vector ac(c.x-a.x,c.y-a.y);

    return cross(ab,ac)/ab.abs();
}

//点到线段距离
double getDistancePS(Point a,Point b,Point c)
{
    //定义4个向量
    Vector ab(b.x-a.x,b.y-a.y);
    Vector ba(a.x-b.x,a.y-b.y);
    Vector ac(c.x-a.x,c.y-a.y);
    Vector bc(c.x-b.x,c.y-b.y);

    if(dot(ab,ac)<0.0) return getDistancePP(a,c);
    if(dot(ba,bc)<0.0) return getDistancePP(b,c);

    return getDistancePL(a,b,c);
}


//线段到线段的距离
double getDistanceSS(Point a,Point b,Point c,Point d)
{
    //从4个点到2线段距离中取最小
    return min(min(getDistancePS(c,d,a),getDistancePS(c,d,b)),min(getDistancePS(a,b,c),getDistancePS(a,b,d)));
}
int main()
{
    int x0,y0,x1,y1,x2,y2,x3,y3;
    cin>>x0>>y0>>x1>>y1>>x2>>y2;
    Point a(x0,y0);
    Point b(x1,y1);
    cout<<"a,b两点间距离"<<getDistancePP(a,b)<<endl;
    Point c(x2,y2);
    cout<<"c点到直线ab距离"<<getDistancePL(a,b,c)<<endl;
    
    cout<<"c点到线段ab的距离"<<getDistancePS(a,b,c)<<endl;
    cin>>x3>>y3;
    
    Point d(x3,y3);
    cout<<"线段ab到线段cd的距离"<<getDistanceSS(a,b,c,d)<<endl;

    return 0;
}