版权声明:转载请注明原作者及出处
1-明确各参数物理含义
m表示发射物质量(kg)
g表示重力加速度(m/s^2)
c表示阻力系数(无量纲),一般取决于炮弹几何外形和雷诺数,参考https://en.wikipedia.org/wiki/Drag_coefficient
a表示空气密度(1.29kg/m^3)
S表示炮弹迎风面积(m^2)
energy表示炮弹离开炮管时具备的动能(J)
theta表示炮弹发射角(rad)
vx0表示炮弹水平x方向初速度(m/s)
vy0表示炮弹竖直y方向初速度(m/s)
2-进行数值计算与作图的mathematica代码
m = 45; *各项数值初始化*
g = 9.8;
c = 0.04;
a = 1.29;
S = 0.02;
k = 0.5*c*a*S;
energy = 32 10^6;
theta = Pi/4;
vx0 = Sqrt[2*energy/m]*Cos[theta];
vy0 = Sqrt[2*energy/m]*Sin[theta];s1 = NDSolve[{ *NDSolve解微分方程组*
vx'[t] == ((-k (vx[t]^2 + vy[t]^2))/m )*Cos[ArcTan[vy[t]/vx[t]]],
vy'[t] == ((-k (vx[t]^2 + vy[t]^2))/m )*Sin[ArcTan[vy[t]/vx[t]]] - g,
x'[t] == vx[t],
y'[t] == vy[t],
vx[0] == vx0, vy[0] == vy0, x[0] == 0, y[0] == 0},
{vx, vy, x, y},
{t, 0, 300}];
ParametricPlot[Evaluate[{x[t], y[t]} /. s1], {t, 0, 150},PlotRange -> {Full, Full}] *将数值解做出参数图*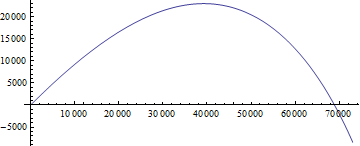
3-可变参数的数值计算与作图的mathematica代码
m = 45; *各项数值初始化*
g = 9.8;
c = 0.04;
a = 1.29;
S = 0.02;
k = 0.5*c*a*S;
energy = 32 10^6;
theta = Pi/4;
vx0 = Sqrt[2*energy/m] Cos[theta];
vy0 = Sqrt[2*energy/m] Sin[theta];
Manipulate[Module[{s1 = NDSolve[{
vx'[t] == ((-k (vx[t]^2 + vy[t]^2))/m)*Cos[ArcTan[vy[t]/vx[t]]],
vy'[t] == ((-k (vx[t]^2 + vy[t]^2))/m)*Sin[ArcTan[vy[t]/vx[t]]] - g,
x'[t] == vx[t],
y'[t] == vy[t],
vx[0] == vx0, vy[0] == vy0, x[0] == 0, y[0] == 0},
{vx, vy, x, y},
{t, 0, 300}]},
ParametricPlot[Evaluate[{x[t], y[t]} /. s1], {t, 0, time},
PlotRange -> {{0, 200000}, {0, 50000}}]],
{k, 0.004*0.5*0.02*1.29, 0.04*0.5*0.02*1.29}, {{time, 150}, 1, 300}]
*设置表示炮弹飞行时间的time参数可变*
*设置表示风阻的k参数可变*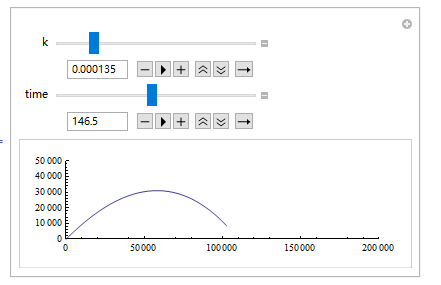
结果显示如上,由于博客内部无法展现mathematica的交互性,需要大家亲自实践才能体会其中的动态变化。
总结
此处考虑了与速度平方成正比的空气阻力,由于各项参数找不到准确值,设置一个可变参数范围,观察炮弹轨迹随着可变参数的变化规律才是最理想的。
最后
以上就是留胡子电话最近收集整理的关于利用mathematica模拟炮弹轨迹的全部内容,更多相关利用mathematica模拟炮弹轨迹内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。

![[HNOI2011]XOR和路径——高斯消元、随机游走模型[HNOI2011]XOR和路径思路代码](https://www.shuijiaxian.com/files_image/reation/bcimg13.png)






发表评论 取消回复