TensorFlow基础之线性回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#!/usr/bin/python
#encoding=utf-8

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

learn_rate = 0.01

#y=2x+4
#随机生成y=2x+4的一些坐标点
train_X = [np.random.randint(20, high=100) for x in range(30)]
train_Y = [2*x+4+np.random.randint(-10, high=10) for x in train_X]

#转成成numpy数组
train_X = np.array(train_X)
train_Y = np.array(train_Y)
n_samples = train_X.shape[0]

#用placeholder定义X和Y变量，具体值在训练的是用feed_dict填充
X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)

#定义初始化W和b，一般不建议置0，用随机值初始化
W = tf.Variable(np.random.random(), name="weigth")
b = tf.Variable(np.random.random(), name="bias")

#带预测的线性方程
prediction = tf.add(tf.multiply(X, W), b)

#用最小二乘定义损失函数
cost = tf.reduce_mean(tf.square(prediction - Y))

#这里优化器并没有用梯度下降，而用的是Adam优化器，后面说明，优化，使得cost最小
#optimizer = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost)
optimizer = tf.train.AdamOptimizer(learn_rate).minimize(cost)

init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    for i in range(1000):
        for (x, y) in zip(train_X, train_Y):
            #执行定义的优化器，填充placeholder定义的变量
            sess.run(optimizer, feed_dict={X:x, Y:y})

        if i % 50 == 0:
            #每隔50次打印一次cost，由于cost依赖X和Y，所以也需要用feed_dict填充
            c = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
            print("Epoch:", '%04d' % i, "cost=", "{:.9f}".format(c), "W=", sess.run(W), "b=", sess.run(b))

    print("Optimization Finished!")

    training_cost = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
    print("Training cost=", training_cost, "W=", sess.run(W), "b=", sess.run(b))

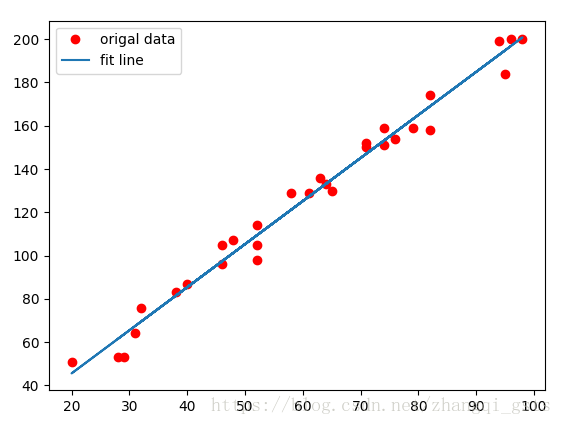
    plt.plot(train_X, train_Y, 'ro', label="origal data")
    plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label="fit line")
    plt.legend()
    plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Epoch: 0000 cost= 4224.109863281 W= 1.0521932 b= 1.1191503
Epoch: 0050 cost= 36.584716797 W= 2.037287 b= 2.5342977
Epoch: 0100 cost= 36.166492462 W= 2.029028 b= 3.1004112
Epoch: 0150 cost= 35.803798676 W= 2.0202172 b= 3.6987798
Epoch: 0200 cost= 35.565029144 W= 2.0129821 b= 4.196062
Epoch: 0250 cost= 35.420043945 W= 2.0074644 b= 4.5785236
Epoch: 0300 cost= 35.332836151 W= 2.0033123 b= 4.8672404
Epoch: 0350 cost= 35.279922485 W= 2.0001948 b= 5.0842767
Epoch: 0400 cost= 35.247253418 W= 1.9978536 b= 5.247259
Epoch: 0450 cost= 35.226734161 W= 1.9960959 b= 5.3696275
Epoch: 0500 cost= 35.213581085 W= 1.9947772 b= 5.4614873
Epoch: 0550 cost= 35.204982758 W= 1.9937861 b= 5.5304694
Epoch: 0600 cost= 35.199237823 W= 1.9930426 b= 5.5822573
Epoch: 0650 cost= 35.195346832 W= 1.9924846 b= 5.6211405
Epoch: 0700 cost= 35.192630768 W= 1.9920651 b= 5.650337
Epoch: 0750 cost= 35.190742493 W= 1.9917507 b= 5.672256
Epoch: 0800 cost= 35.189373016 W= 1.9915143 b= 5.688697
Epoch: 0850 cost= 35.188400269 W= 1.9913368 b= 5.7010508
Epoch: 0900 cost= 35.187698364 W= 1.9912037 b= 5.710329
Epoch: 0950 cost= 35.187175751 W= 1.9911035 b= 5.717318
Optimization Finished!
Training cost= 35.186806 W= 1.9910296 b= 5.7224526

1
2
3
Epoch: 0000 cost= inf W= -9.956399e+27 b= -1.1271411e+26
Epoch: 0001 cost= nan W= nan b= nan
Epoch: 0002 cost= nan W= nan b= nan