目录
回溯法基本步骤
问题描述
基本思路
具体实现代码
运行结果
回溯法基本步骤
(1)对所给的问题,定义问题的解空间。
(2)确定状态空间树的结构
(3) 用深度优先(DFS)的方法搜索解空间,用约束方程和目标函数的界对状态空间树进行修剪,生成搜索树,得到问题的解。
参考:《算法分析与设计(第三版)》(清华大学出版社,郑宗汉、郑晓明编著)
问题描述
0/1背包问题用通俗易懂的话来描述就是:给定一个背包可承受的最大重量、各个物品的重量和价值,求在不超重的情况背包内所装物品的最大总价值和达到该最大值物品的选择情况。
基本思路
根据问题要求,显然约束方程如下:
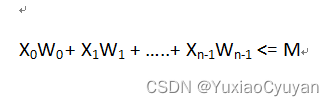
(博客水平有限,只能插入图片望谅解)
其中,X为货物的选择情况(0为不选,1为选),W为货物的重量,M为背包最大容量,n为货物的个数(由于存在数组中,则第n个货物下标为n-1),下标为货物在数组中的下标。
目标函数如下:
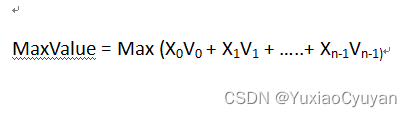
其中V为货物价值。
简单分析可知,n个货物的0/1背包问题的状态空间树是一课高度为n的完全二叉树,结点总数为2^n+1 - 1。可以假定第i层结点的左孩子(也就是左孩子在第i+1层)代表选第i个货物,右孩子代表不选第i个货物,结点的值为当前的货物重量。搜索过程中如果不能沿着左孩子前进,则回溯,把搜索转移到右孩子。
这里有两个学习过程的疑惑(如果能有大佬解答的话就太感谢了):
1.既然回溯法是蛮力法的改进,那么如果是蛮力法的话如果不能沿着左孩子结点继续前进时(不满足约束方程),还是沿着子树得一直走完(列出所有的解);回溯法则是不满足约束方程则回溯? 是这个区别吗?
2.虽然能根据问题需求列出二叉树,那么是用二叉树的数据结构吗?
具体实现代码
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<Windows.h>
#include<malloc.h>
#define N 100
//定义货物的结构体数组
typedef struct {
int weight;//重量
int value;//价值
int flag;//标记是否选择(0、1)
}Goods[N];
//定义全局变量
int n;//物品数量
int M;//背包容量
int MaxValue;//目标函数的值
int choose[N];//记录最大价值货物选择的解向量,0为不选,1为选
//初始化
void Init(Goods& goods) {
printf("物品数量和背包容量:");
scanf("%d %d", &n, &M);
for (int i = 0;i < n;i++) {
printf("第%d个物品的重量和价值:", i + 1);
scanf("%d %d", &goods[i].weight, &goods[i].value);
goods[i].flag = 0;
}
}
//判断是否满足约束方程
bool isOverweight(Goods& goods, int m) {
int sum_w = 0;
for (int i = 0;i <= m;i++) {
sum_w += goods[i].flag * goods[i].weight;
}
if (sum_w > M) {
return false;
}
return true;
}
void KnapSack(Goods& goods, int m, int n) {
//m代表货物的下标,调用函数时m一般为0(从第一个货物开始)
int i = 0;
int j = 0;
int sum_v = 0;//临时变量记录当前解下的总价值
//递归的终止条件
if (m == n) {
for (i = 0;i < m;i++) {
sum_v += goods[i].value * goods[i].flag;
}
if (sum_v > MaxValue) {
MaxValue = sum_v;//如果该解大于目标函数值,则将该解更新为最大值
for (int i = 0;i < n;i++) {
choose[i] = goods[i].flag;//记录当前解向量
}
}
}
else {
for (j = 0;j < 2;j++) {
goods[m].flag = j;//flag取值为0、1
if (isOverweight(goods, m)) {
//如果满足约束方程则递归至下一个货物
KnapSack(goods, m + 1, n);
}
}
}
}
int main() {
Goods goods;
Init(goods);
KnapSack(goods, 0, n);
printf("最大价值为:%dn", MaxValue);
printf("解向量为:");
for (int i = 0;i < n;i++) {
printf("%d ", choose[i]);
}
system("pause");
return 0;
}运行结果
输入例子:weight[ ] = { 2,3,6,5,4 } value[ ] = { 6,4,5,4,7 }
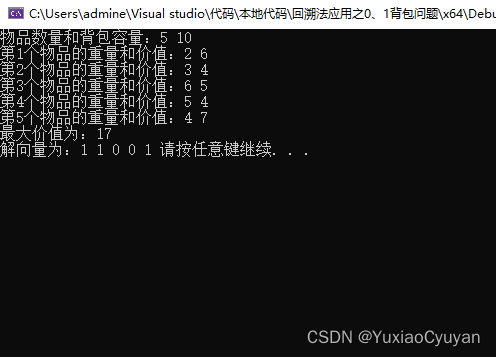
该思路及代码参考来源:https://blog.csdn.net/Blackoutdragon/article/details/116097743
(ps:笔者为初学者,如有错误,敬请指正,望谅解!谢谢各位)
最后
以上就是真实羽毛最近收集整理的关于回溯法解决0/1背包问题(C语言实现)的全部内容,更多相关回溯法解决0/1背包问题(C语言实现)内容请搜索靠谱客的其他文章。








发表评论 取消回复