熵值法是一种基于信息熵理论的客观赋值方法。即数据越离散,所含信息量越多,对综合评价影响越大。
目录
- 一、基于面板数据熵值法介绍
- 二、R语言实现
- 参考文献
一、基于面板数据熵值法介绍
传统的熵值法有个弊端,只能针对于截面数据,即根据某一年 k k k个地区 j j j项指标进行综合评价。而在实际处理经济型数据过程中,经常会遇到面板数据。即根据 m m m个年份, k k k个区县, j j j项指标对其进行综合评价。其具体过程如下(与传统的熵值法过程非常相似,主要是第二步和第三步有区别):
(1) 指标标准化处理
正向指标 Z α i j = x α i j − x m i n x m a x − x m i n text{正向指标}Z_{alpha ij}=frac{x_{alpha ij}-x_{min}}{x_{max}-x_{min}} 正向指标Zαij=xmax−xminxαij−xmin 负向指标 Z α i j = x m a x − x α i j x m a x − x m i n text{负向指标}Z_{alpha ij}=frac{x_{max}-x_{alpha ij}}{x_{max}-x_{min}} 负向指标Zαij=xmax−xminxmax−xαij 式中, x m a x mathit{x_{max}} xmax, x m i n mathit{x_{min}} xmin分别代表第 j mathit{j} j项指标的最大值和最小值; x α i j x_{alpha ij} xαij, z α i j z_{alpha ij} zαij分别代表第 j mathit{:j:} j项指标标准化处理前和处理后的值。
(2) 指标归一化
P
α
i
j
=
Z
α
i
j
∑
α
=
1
m
∑
i
=
1
k
Z
α
i
j
P_{alpha ij}=frac{Z_{alpha ij}}{sumlimits_{alpha=1}^{m}sumlimits_{i=1}^{k}Z_{alpha ij}}
Pαij=α=1∑mi=1∑kZαijZαij
(3) 计算熵值
E
j
=
−
k
1
∑
α
=
1
m
∑
i
=
1
k
P
α
i
j
l
n
P
α
i
j
E_{j}=-k_{1}sumlimits_{alpha=1}^{m}sumlimits_{i=1}^{k}P_{alpha ij}ln{P_{alpha ij}}
Ej=−k1α=1∑mi=1∑kPαijlnPαij
其中,
k
1
=
1
l
n
(
m
×
k
)
k_{1}=displaystylefrac{1}{ln(m times k)}
k1=ln(m×k)1
(4) 计算各项指标的冗余度
D
j
=
1
−
E
j
D_{mathit{j}}=1-E_{mathit{j}}
Dj=1−Ej
(5) 计算各项指标权重
W
j
=
D
j
∑
j
=
1
n
D
j
W_{mathit{j}}=frac{D_{mathit{j}}}{sumlimits_{mathit{j=1}}^{n}D_{mathit{j}}}
Wj=j=1∑nDjDj
(6) 得到各区县的综合经济指数
I
α
i
=
P
α
i
j
×
W
j
I_{alpha i}=P_{mathit{alpha ij}} times W_{mathit{j}}
Iαi=Pαij×Wj
二、R语言实现
以重庆市各区县为例,选取如下九项指标数据构建综合经济指数,数据来源《重庆统计年鉴》,时间范围为2009-2018年。
| 一级指标 | 二级指标 |
| 经济实力 | GDP(国民生产总值) |
| 全社会固定资产投资 | |
| 社会消费品总额 | |
| 经济质量 | 第三产业/GDP |
| 人均GDP | |
| 区县一般公共收入/GDP | |
| 社会生活 | 农村居民人均纯收入 |
| 人均一般公共服务支出 | |
| 城镇居民人均可支配收入 |
部分数据展示如下:
代码如下:
#根据数据实际情况,修改初始参数
setwd('C:/Users/dell/Desktop')
library(xlsx)
k=38 #区县个数
m=10 #年份
n=9 #指标个数
#读取数据
data.list=list()
for(i in seq(n))
data.list[[i]]=read.xlsx('df.xlsx',sheetIndex = i,encoding='UTF-8')
caculate_p<-function(x) {
z<-(x[,-1]-min(x[,-1]))/(max(x[,-1])-min(x[,-1]))
p<-z/(sum(z))
}
P<-lapply(data.list,caculate_p)
caculate_d<-function(x){
a<-x*log(x)
a[is.na(a)]<-0
d<-(1-(-sum(a)/log(k*m)))
}
d<-sapply(P,caculate_d)
#输出权重
w<-sapply(d,function(x) {x/sum(d)})
print(w)
#得到每年九个指标的Pij
rank=list()
data=data.frame(matrix(0,k,0))
for(j in seq(m))
{ for(i in seq(n))
{
data[paste0("指标",i)]=as.vector(P[[i]][,j])
rank[[j]]=data
}
}
#写出各年区县的综合经济指数
year=2018
for(i in seq(length(rank)))
{
score<-as.matrix(rank[[i]]) %*% w #计算各区县综合指数
county_score<-data.frame(cbind(as.character(data.list[[1]][,1]),score)) #添加区县名
colnames(county_score)<-c("区县",'综合经济指数')
write.xlsx(county_score,file='rank.xlsx',sheetName=paste0(year,'年'),append=TRUE,row.names=F)
cat(paste0(year,'年写入完毕n'))
year<-year-1
}
写出的文件则是2009-2018年各区县的综合经济指数。
各指标权重占比依次为(GDP、社会消费品总额、…)
生成各年份各区县的综合经济指数如下图所示:
注意:
1、代码中的k、m、n参数根据实际数据进行修改
2、需要将数据文件放置R的工作路径中
由于原指数太小,对其乘以
1
0
4
10^{4}
104,绘制2009年和2018年各区县的综合经济指数柱形图:
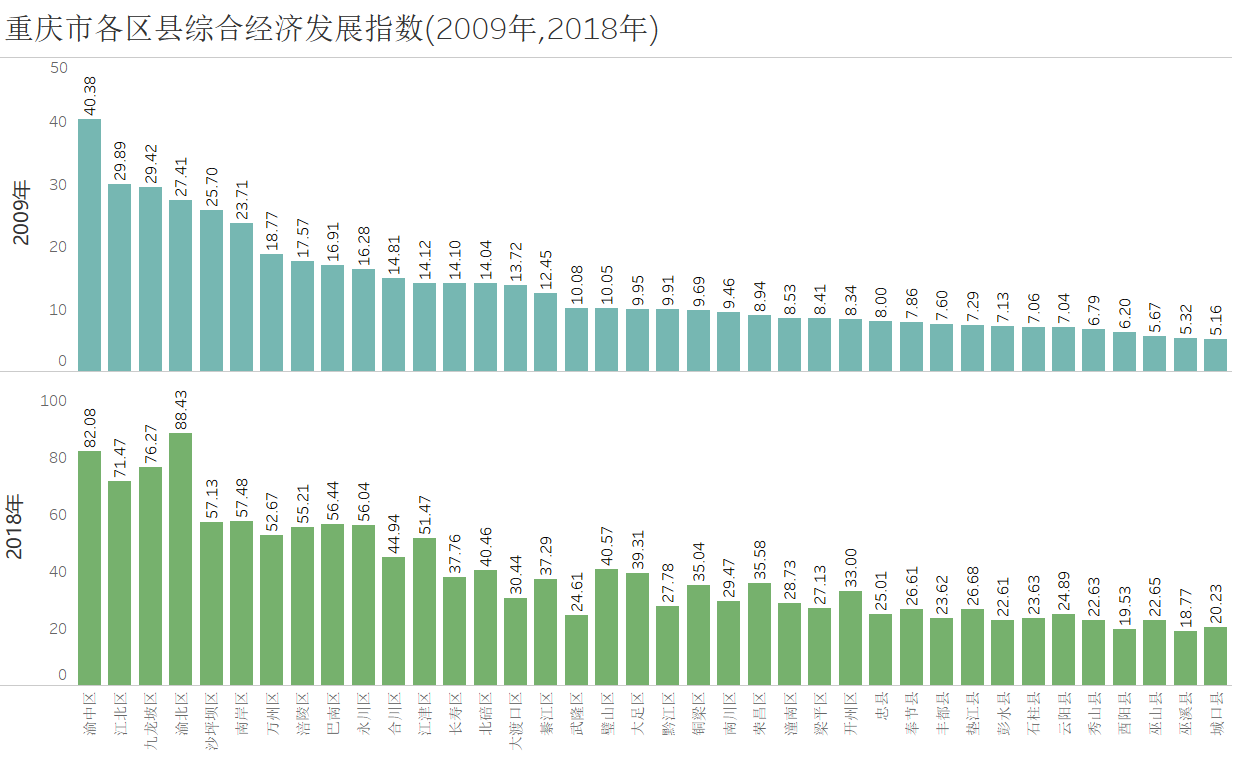
从上图不难看出:
1、2018年各区县的综合经济发展指数明显要大于2009年各区县的综合经济发展指数,说明10年来重庆市各区县经济得到了较大的发展。
2、渝中区、江北区、九龙波区、渝北区综合经济发展水平较高,而城口县、巫溪县、巫山县、酉阳县经济发展水平较低
参考文献
[1]冯兴华,钟业喜,李峥荣,傅钰.长江经济带城市体系空间格局演变[J].长江流域资源与环境,2017,26(11):1721-1733.
后续将会将熵值法应用到空间相关分析中,敬请期待~
最后
以上就是瘦瘦跳跳糖最近收集整理的关于基于面板数据的熵值法介绍与实现的全部内容,更多相关基于面板数据内容请搜索靠谱客的其他文章。








发表评论 取消回复