本篇讨论的主题是在平面坐标系中如何将一个坐标系(目标坐标系,以下简称目标系)中的所有点投射到另一个坐标系(基坐标系)中。平面坐标系之间的转化一般有三步操作:1、平移;2、旋转;3、拉伸。
在转化的过程中需要的几个已知条件分别是:1、目标系的一个已知点(特征点A)对应于基坐标系中的点(特征点A’)。2、目标系的原点(O)对应于基坐标系中的原点(O')。3、基座标系的原点(O‘’)。
一、坐标系拉伸
①、计算两坐标系X和Y轴分别对应的拉伸比例:
②、将A点按缩放比例映射到基坐标系中(A''):
二、坐标系旋转和平移
①:坐标系旋转
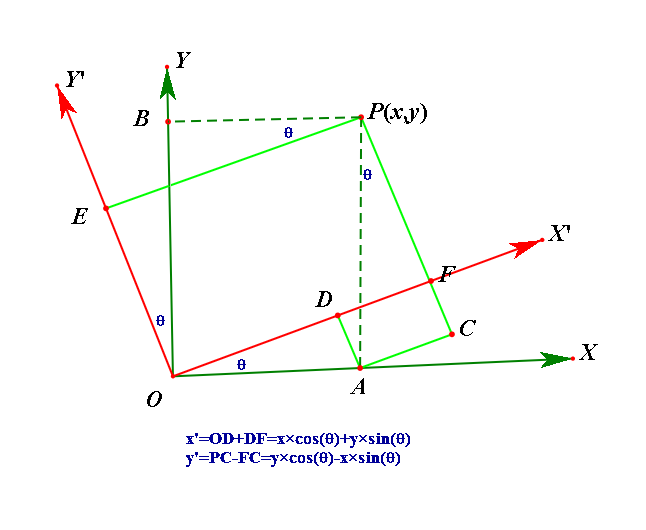
②坐标系平移加旋转
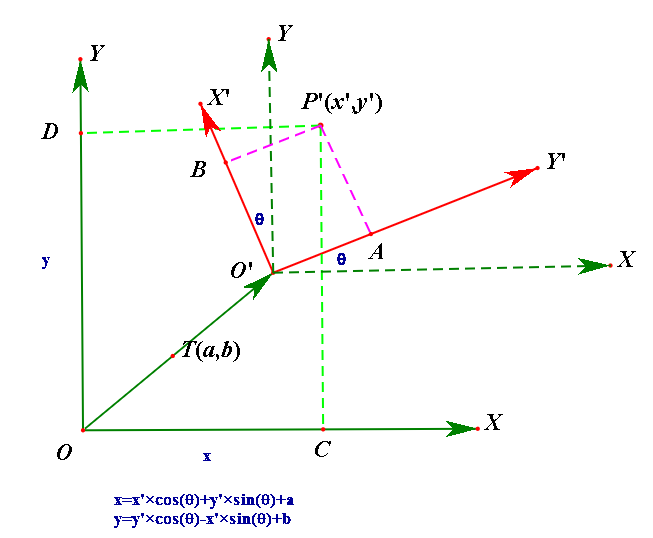
③得出公式
根据坐标系旋转和平移的规则,可以得出公式
我们的目标是求出θ。
设m = cos(θ),n=sin(θ),根据已知量可得出公式:
得出方程组的增广矩阵,根据高斯消除元法即可求得m,n:
再根据反三角函数求得θ,此时θ、a、b、T(坐标系倍数)的值都已经得到。
故任意目标系坐标(x、y)可通过公式映射到基坐标系(f(x)、f(y)):
C#代码:
public class CoorPoint
{
public double x { get; set; }
public double y { get; set; }
public CoorPoint()
{ }
public CoorPoint(double x, double y)
{
this.x = x;
this.y = y;
}
public CoorPoint(CoorPoint pt)
{
this.x = pt.x;
this.y = pt.y;
}
public static CoorPoint operator +(CoorPoint src, CoorPoint tar)
{
CoorPoint result = new CoorPoint(src);
result.x += tar.x;
result.y += tar.y;
return result;
}
public static CoorPoint operator -(CoorPoint src, CoorPoint tar)
{
CoorPoint result = new CoorPoint(src);
result.x -= tar.x;
result.y -= tar.y;
return result;
}
public static CoorPoint operator /(CoorPoint src, CoorPoint tar)
{
CoorPoint result = new CoorPoint(src);
result.x /= tar.x;
result.y /= tar.y;
return result;
}
public static CoorPoint operator *(CoorPoint src, CoorPoint tar)
{
CoorPoint result = new CoorPoint(src);
result.x *= tar.x;
result.y *= tar.y;
return result;
}
}
class CoordinateSystemChg
{
/// <summary>
/// 基坐标系:特征点(A')
/// </summary>
public CoorPoint baseCoor_basePoint { get; set; }
/// <summary>
/// 基坐标系:原点(O)
/// </summary>
public CoorPoint baseCoor_originPoint { get; set; }
/// <summary>
/// 现实坐标系:特征点(A)
/// </summary>
public CoorPoint realistic_basePoint { get; set; }
/// <summary>
/// 现实坐标系对应基坐标系拉伸后的点(A'')
/// </summary>
public CoorPoint realistic_basePointAfterZoom { get; set; }
/// <summary>
/// 现实坐标系:原点(O)
/// </summary>
public CoorPoint realistic_originPoint { get; set; }
/// <summary>
/// 现实坐标系对应基坐标系:原点(O')
/// </summary>
public CoorPoint realistic_originAsBaseCoorPoint { get; set; }
//定义原点时 已经统一缩放比例
//第一步的结果
//位移量:a(x轴),b(y轴)
double a = 0;
double b = 0;
//坐标系倍数
CoorPoint coorTimes;
//坐标系夹角
double offsetAngle;
//第一步:得到坐标系之间的角度θ
/// <summary>
/// 计算出两坐标系的X,Y比例
/// </summary>
public void GetSale()
{
coorTimes = (realistic_basePoint - realistic_originPoint) / (baseCoor_basePoint - realistic_originAsBaseCoorPoint);
if (coorTimes.x < 0)
coorTimes.x = -coorTimes.x;
if (coorTimes.y < 0)
coorTimes.y = -coorTimes.y;
}
/// <summary>
/// ①按比例缩放(实际坐标系的基点),使之与基坐标系统一
/// </summary>
public void DoZoom()
{
realistic_basePointAfterZoom = realistic_basePoint / coorTimes;
}
/// <summary>
/// ②得到偏移角,入参实际坐标系原点坐标在基坐标系上的坐标
/// </summary>
public void GetOffsetAngle()
{
double[] x = new double[2];
a = (realistic_originAsBaseCoorPoint.x - baseCoor_originPoint.x);
b = (realistic_originAsBaseCoorPoint.y - baseCoor_originPoint.y);
double[,] g = {
{ realistic_basePointAfterZoom.x, realistic_basePointAfterZoom.y, (baseCoor_basePoint.x - a) },
{ realistic_basePointAfterZoom.y, -realistic_basePointAfterZoom.x, (baseCoor_basePoint.y - b) }
};
GaussianElimination(g, x);
// x[0]:θ角的余弦值;x[1]:θ角的正弦值
offsetAngle = Math.Acos(x[0]);
Console.WriteLine(x[0] + ":" + Math.Acos(x[0]));
Console.WriteLine(x[1] + ":" + Math.Asin(x[1]));
}
//第二步:根据θ角求出在基坐标系中点的映射
/// <summary>
/// 将实际坐标系中的点转换到基坐标系中的点
/// </summary>
/// <param name="src"></param>
/// <param name="rlt"></param>
public void GetCoordinateBaseSystem(CoorPoint src, out CoorPoint rlt)
{
double db1 = Math.Cos(offsetAngle);
double db2 = Math.Sin(offsetAngle);
rlt = new CoorPoint();
rlt.x = ((src.x / coorTimes.x) * Math.Cos(offsetAngle) + (src.y / coorTimes.y) * Math.Sin(offsetAngle) + a);
rlt.y = ((src.y / coorTimes.y) * Math.Cos(offsetAngle) - (src.x / coorTimes.x) * Math.Sin(offsetAngle) + b);
}
/// <summary>
/// 将基坐标系中的点转换到实际坐标系中的点
/// </summary>
/// <param name="src"></param>
/// <param name="rlt"></param>
public void GetCoordinateRealisticSystem(CoorPoint src, out CoorPoint rlt)
{
double[] x = new double[2];
double[,] g = {
{
Math.Cos(offsetAngle), Math.Sin(offsetAngle),(src.x - a)*coorTimes.x },
{ -Math.Sin(offsetAngle), Math.Cos(offsetAngle),(src.y - b)*coorTimes.y }
};
GaussianElimination(g, x);
rlt = new CoorPoint();
rlt.x = x[0];
rlt.y = x[1];
}
#region 数学方法
//简单的高斯消元法;
//输入要求解的扩展矩阵g[m,n];和存放结果的数组x[n];
//返回值为计算结果数组x[n];
public static double[] GaussianElimination(double[,] g, double[] x)
{
int m = g.GetLength(0);//获得扩展矩阵的行(方程个数);
int n = g.GetLength(1);//获得扩展矩阵的列(未知数个数+1);
//========================================================
//消元过程;
for (int i = 1; i < m; i++)
{
for (int j = i; j < m; j++)
{
for (int k = n - 1; k > i - 2; k--)
{
g[j, k] = g[j, k] - (g[j, i - 1] / g[i - 1, i - 1]) * (g[i - 1, k]);
}
}
}
//回代过程;
//第一步:翻转;
//换行;
double tem;
for (int i = 0; i < m / 2; i++)
for (int j = 0; j < n; j++)
{
tem = g[i, j];
g[i, j] = g[m - i - 1, j];
g[m - i - 1, j] = tem;
}
//倒序
for (int i = 0; i < m; i++)
for (int j = 0; j < n / 2; j++)
{
tem = g[i, j];
g[i, j] = g[i, n - 2 - j];
g[i, n - 2 - j] = tem;
}
//第二步:消元;
for (int i = 1; i < m; i++)
{
for (int j = i; j < m; j++)
{
for (int k = n - 1; k > i - 2; k--)
{
g[j, k] = g[j, k] - (g[j, i - 1] / g[i - 1, i - 1]) * (g[i - 1, k]);
}
}
}
//第三步:翻回;
//重新换行;
for (int i = 0; i < m / 2; i++)
for (int j = 0; j < n; j++)
{
tem = g[i, j];
g[i, j] = g[m - i - 1, j];
g[m - i - 1, j] = tem;
}
//重新倒序;
for (int i = 0; i < m; i++)
for (int j = 0; j < n / 2; j++)
{
tem = g[i, j];
g[i, j] = g[i, n - 2 - j];
g[i, n - 2 - j] = tem;
}
//取结果(这里是正序结果哦);
for (int i = 0; i < m; i++)
x[i] = g[i, n - 1] / g[i, i];
return x;//返回计算结果;
}
#endregion
}
最后
以上就是正直高跟鞋最近收集整理的关于不同平面直角坐标系之间的转换公式的推导及C#代码实现的全部内容,更多相关不同平面直角坐标系之间内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。
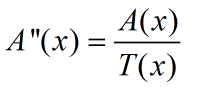
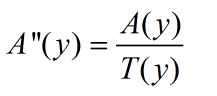
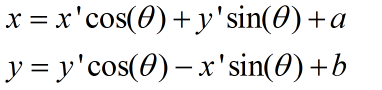
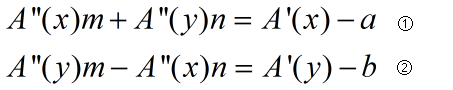
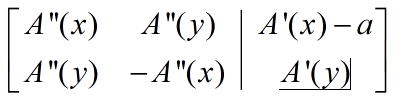
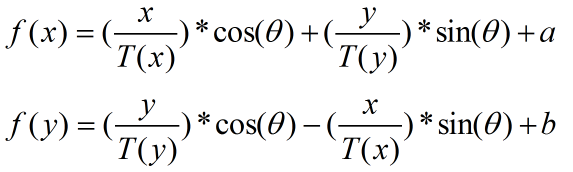








发表评论 取消回复