题目
传送门
题解
扫描线段的经典题:矩形面积求交 摘自最好的线段树总结
考虑下图中的四个矩形:
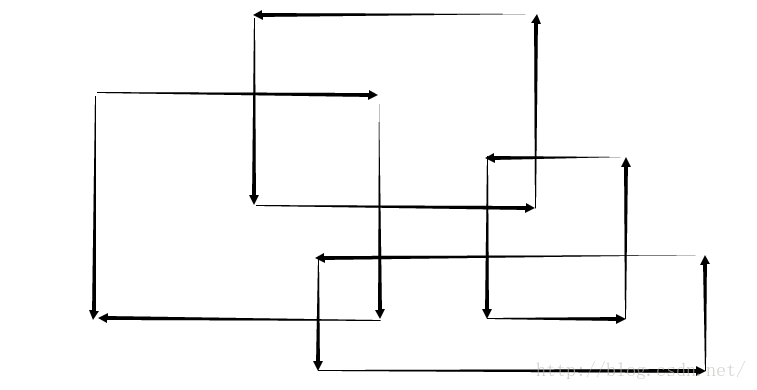

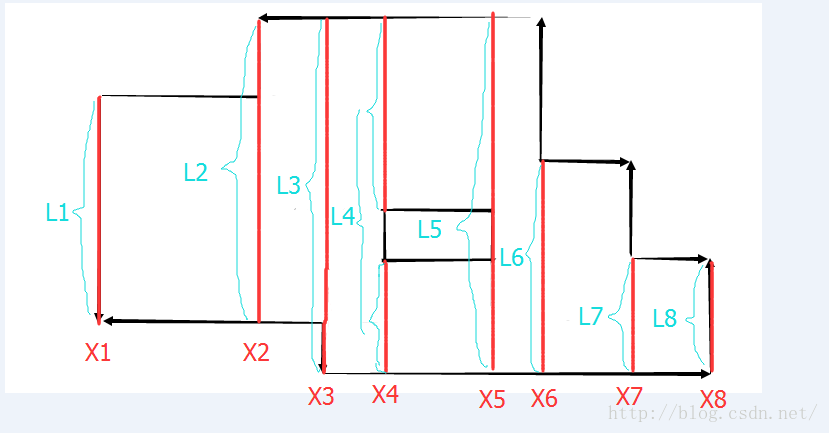
观察第三个图:
扫描线的思路:使用一条垂直于X轴的直线,从左到右来扫描这个图形,明显,只有在碰到矩形的左边界或者右边界的时候,
这个线段所扫描到的情况才会改变,所以把所有矩形的入边,出边按X值排序。然后根据X值从小到大去处理,就可以
用线段树来维护扫描到的情况。如上图,X1到X8是所有矩形的入边,出边的X坐标。
而红色部分的线段,是这样,如果碰到矩形的入边,就把这条边加入,如果碰到出边,就拿走。红色部分就是有线段覆盖的部分。
要求面积,只需要知道图中的L1到L8。而线段树就是用来维护这个L1到L8的。
扫描线算法流程:
X1:首先遇到X1,将第一条线段加入线段树,由线段树统计得到线段长度为L1.
X2:然后继续扫描到X2,此时要进行两个动作:
1.计算面积,目前扫过的面积=L1*(X2-X1)
2.更新线段。由于X2处仍然是入边,所以往线段树中又加了一条线段,加的这条线段可以参考3幅图中的第一幅。
然后线段树自动得出此时覆盖的线段长度为L2 (注意两条线段有重叠部分,重叠部分的长度只能算一次)
X3:继续扫描到X3,步骤同X2
先计算 扫过的面积+=L2*(X3-X2)
再加入线段,得到L3.
X4:扫描到X4有些不一样了。
首先还是计算 扫过的面积+=L3*(X4-X3)
然后这时遇到了第一个矩形的出边,这时要从线段树中删除一条线段。
删除之后的结果是线段树中出现了2条线段,线段树自动维护这两条线段的长度之和L4
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
const int maxn=500;
int n;
double x1,x2,y1,y2;
struct Tree{
int l,r,c;
double cnt,fl,fr;//cnt浮点的差值
}tree[maxn<<2];
struct Line{
double x,y1,y2;
int f;//+-1:矩形左边还是右边的边
}line[maxn<<1];
double y[maxn];
bool cmp(Line a,Line b) {return a.x<b.x;}
void build_tree(int l,int r,int rt)
{
tree[rt].l=l; tree[rt].r=r;
tree[rt].c=tree[rt].cnt=0;
tree[rt].fl=y[l];
tree[rt].fr=y[r];
if (l+1==r) return;//叶子结点
int mid=(l+r)>>1;
build_tree(l,mid,rt<<1);
build_tree(mid,r,rt<<1|1);
}
void calc(int rt)
{
if (tree[rt].c>0)
{
tree[rt].cnt=tree[rt].fr-tree[rt].fl;
return;
}
if (tree[rt].l+1==tree[rt].r) tree[rt].cnt=0;//叶子节点
else tree[rt].cnt=tree[rt<<1].cnt+tree[rt<<1|1].cnt;
}
void update(int rt,Line e)
{
if (e.y1==tree[rt].fl && e.y2==tree[rt].fr)
{
tree[rt].c+=e.f;
calc(rt);
return;
}
if (e.y2<=tree[rt<<1].fr) update(rt<<1,e);
else if (e.y1>=tree[rt<<1|1].fl) update(rt<<1|1,e);
else
{
Line tmp=e;
tmp.y2=tree[rt<<1].fr;
update(rt<<1,tmp);
tmp=e;
tmp.y1=tree[rt<<1|1].fl;
update(rt<<1|1,tmp);
}
calc(rt);
}
int main()
{
int ans=0;
while (scanf("%d",&n) && n)
{
ans++;
int tot=0;
for (int i=1; i<=n; i++)
{
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
line[++tot].x=x1;
line[tot].y1=y1;
line[tot].y2=y2;
line[tot].f=1;
y[tot]=y1;
line[++tot].x=x2;
line[tot].y1=y1;
line[tot].y2=y2;
line[tot].f=-1;
y[tot]=y2;
}
sort(y+1,y+1+tot);
sort(line+1,line+1+tot,cmp);
build_tree(1,tot,1);
update(1,line[1]);
double res=0;
for (int i=2; i<=tot; i++)//tot和n总混
{
res+=tree[1].cnt*(line[i].x-line[i-1].x);
update(1,line[i]);
}
printf("Test case #%dn",ans);
printf("Total explored area: %.2fnn",res);
}
return 0;
}
/*
2
10 10 20 20
15 15 25 25.5
0
Test case #1
Total explored area: 180.00
*/辣鸡poj%.2lf输出不对只有%.2f
还要输出两个nn不然PE
最后
以上就是结实电源最近收集整理的关于[poj1151]Atlantis矩形面积求交(扫描线+线段树)的全部内容,更多相关[poj1151]Atlantis矩形面积求交(扫描线+线段树)内容请搜索靠谱客的其他文章。




![[poj1151]Atlantis矩形面积求交(扫描线+线段树)](https://file2.kaopuke.com:8081/files_image/reation/bcimg4.png)



发表评论 取消回复