Optimal Strategy 组合数，dp，博弈论（济南）

90 阅读 0 评论 60 点赞

我是靠谱客的博主迷人航空，最近开发中收集的这篇文章主要介绍Optimal Strategy 组合数，dp，博弈论（济南），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在这里插入图片描述
题意：

有n个数，E和M轮流取，使各自取到的值之和最大，最优策略，问取数的过程有多少种

思路：

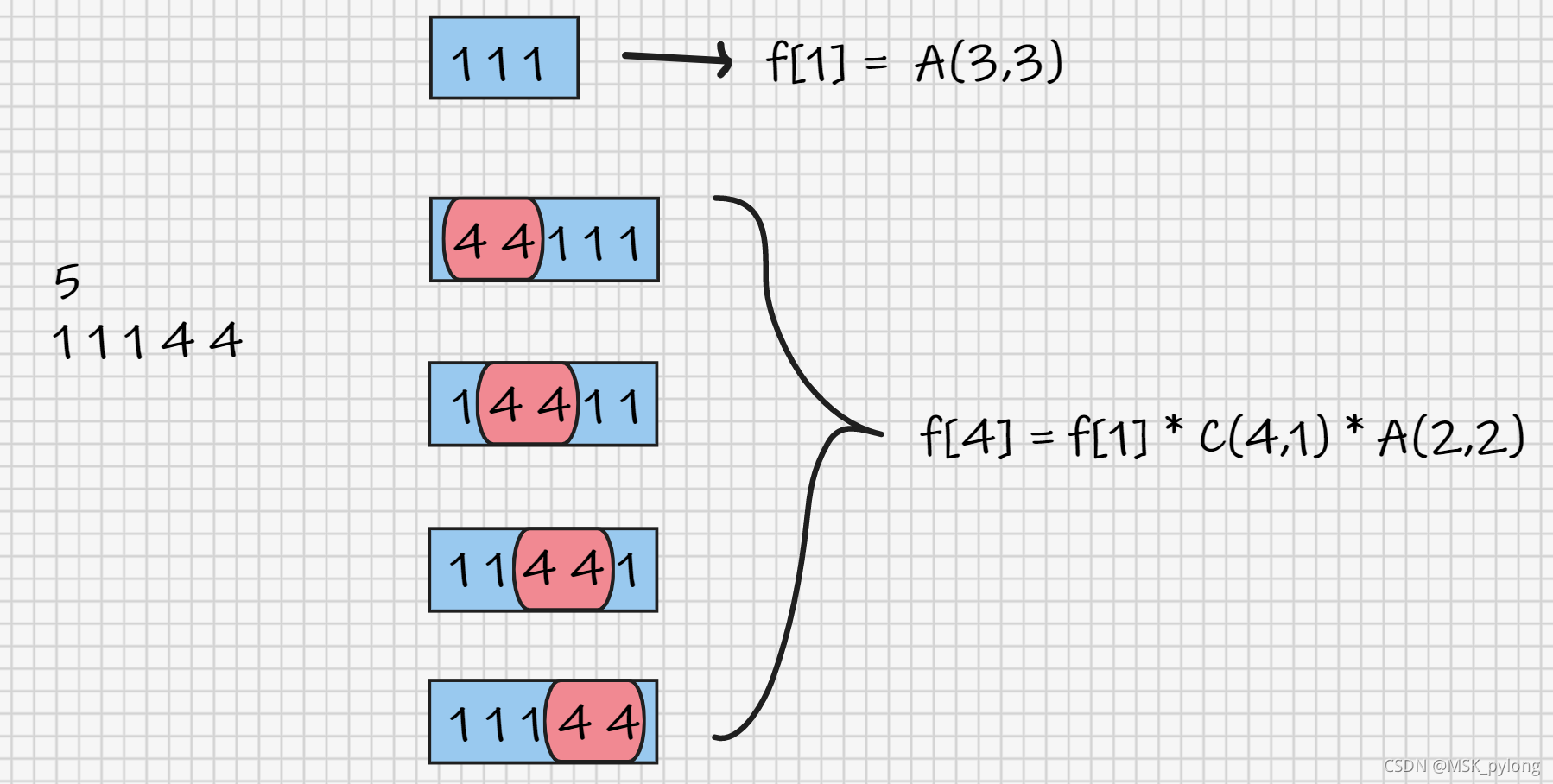
分析样例可知不能贪心的去做，不一定每回合玩家都拿最大的，而是与每回合剩余的数中最大的有关，那么就是与每个值的个数有关，又进一步想到是与每个值的个数的奇偶性有关
值为i的元素，那么所有小于i的元素都不必再按两两配对考虑，因为它们任何一个都不是此时序列中的最大值，可以任意顺序取走

#include <iostream>
#define endl 'n'

using namespace std;

typedef long long ll;

const int N = 1e6 + 50, M = 1e6 + 100;
const ll mod = 998244353;

ll n;
ll f[N];
ll cnt[N], sum[N];

ll fac[M], inv[M];

int power(int a, int b)
{
    int ret;
    if (b == 0) return 1;
    ret = power(a, b / 2);
    ret = 1ll * ret * ret % mod;
    if (b % 2) ret = 1ll * ret * a % mod;
    return ret;
}

void init()
{
    fac[0] = 1, inv[0] = 1;
    for (int i = 1; i <= 1000000; i ++ )
    {
        fac[i] = 1ll * fac[i - 1] * i % mod;
        inv[i] = power(fac[i], mod - 2);
    }
}

int C(int n, int m)
{
    if (n < m) return 0;
    if (n < 0 || m < 0) return 0;
    return 1ll * fac[n] * inv[m] % mod * inv[n - m] % mod;
}

void solve()
{
    cin >> n;
    for (int i = 1, x; i <= n; i ++ ) cin >> x, cnt[x] ++ ;

    for (int i = 1; i <= n; i ++ ) sum[i] = sum[i - 1] + cnt[i];

    bool flag = false;
    for (int i = 1; i <= n; i ++ )
    {
        if (!cnt[i])
        {
            f[i] = f[i - 1];
            continue;
        }

        if (!flag)
        {
            flag = true;
            f[i] = 1;
            for (int j = 2; j <= cnt[i]; j ++ ) f[i] = (f[i] * j) % mod;
            continue;
        }

        f[i] = f[i - 1] * C(sum[i - 1] + cnt[i] / 2, sum[i - 1]) % mod;
        for (int j = 2; j <= cnt[i]; j ++ ) f[i] = (f[i] * j) % mod;
    }

    cout << f[n] << endl;
}

int main()
{
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    
    int _ = 1;
//    cin >> _;
    
    while (_ --)
    {
        init();
        solve();
    }
    
    return 0;
}