1. 首页
  2. 文章中心
  3. 数学建模

2.3-非平稳时间序列分析总结

121 阅读 0 评论
我是靠谱客的博主 悲凉康乃馨，这篇文章主要介绍2.3-非平稳时间序列分析总结，现在分享给大家，希望可以做个参考。

时间序列分析

第三节 非平稳时间序列分析

一般，我们得到的序列都是非平稳序列。
这便要求我们对其进行处理。

  • 非平稳序列变为平稳序列（利用差分运算）
  • ARIMA模型的拟合

3.1 非平稳序列变为平稳序列（利用差分运算）

  • 序列显著线性趋势-一阶差分
    例题1 1964年—1999年中国纱年产量序列蕴含着一个近似线性的递增趋势。对该序列进行一阶差分运算。

代码:

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
goptions vsize=10cm hsize=10cm;
data a;
input year sha;
dif=dif(sha);/*一阶差分*/
cards;
1964    97
1965    130
1966    156.5
1967    135.2
1968    137.7
1969    180.5
1970    205.2
1971    190
1972    188.6
1973    196.7
1974    180.3
1975    210.8
1976    196
1977    223
1978    238.2
1979    263.5
1980    292.6
1981    317
1982    335.4
1983    327
1984    321.9
1985    353.5
1986    397.8
1987    436.8
1988    465.7
1989    476.7
1990    462.6
1991    460.8
1992    501.8
1993    501.5
1994    489.5
1995    542.3
1996    512.2
1997    559.8
1998    542
1999    567
;
proc gplot;
plot sha*year;
plot dif*year;
symbol v=star c=blue i=join;
run;

结果图：
原始序列图：
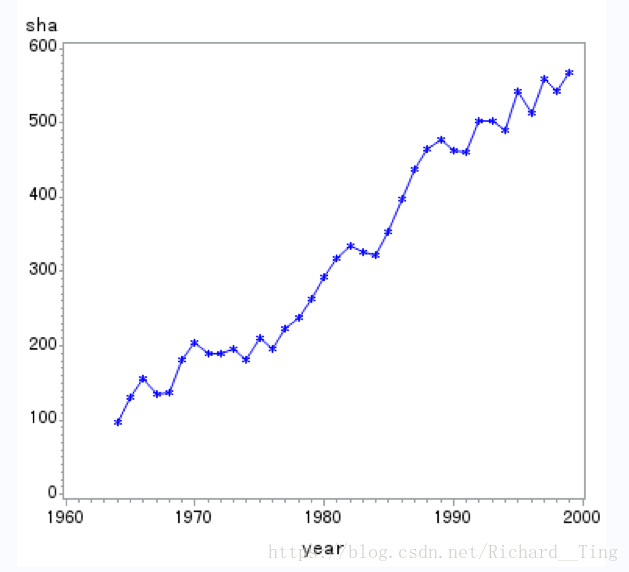
这里写图片描述
一阶差分：
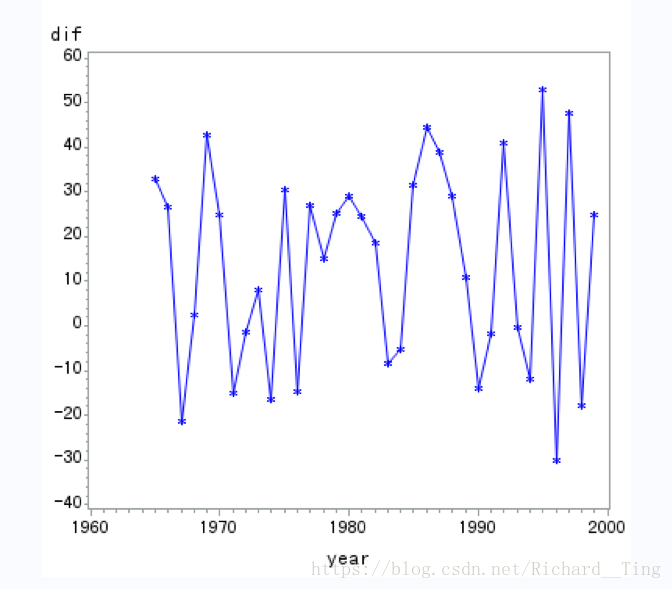
这里写图片描述

  • 序列蕴含曲线趋势-通常低阶（二阶、三阶）差分
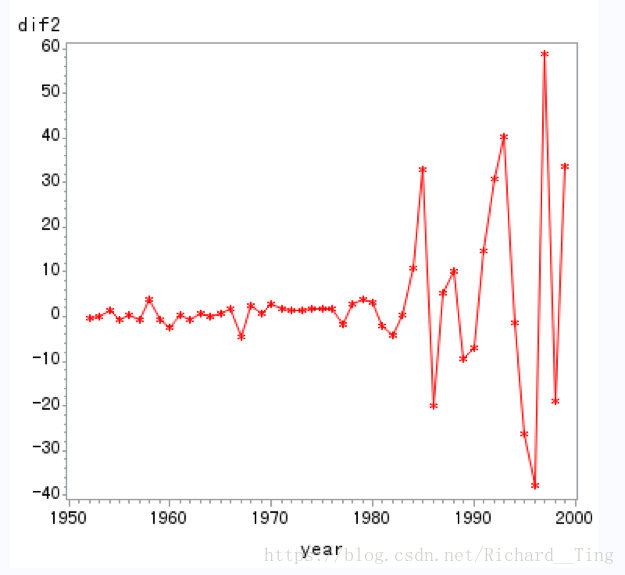
    例题2 尝试提取1950年—1999年北京市民用车辆拥有量序列的确定性信息。
    代码：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
data a;
input year x;
dif1=dif(x);
dif2=dif(dif1);/*2阶差分*/
cards;
1950    5.43
1951    6.19
1952    6.63
1953    7.18
1954    8.95
1955    10.14
1956    11.74
1957    12.6
1958    17.26
1959    21.07
1960    22.38
1961    24
1962    24.8
1963    26.13
1964    27.61
1965    29.95
1966    33.92
1967    33.21
1968    34.8
1969    37.16
1970    42.41
1971    49.44
1972    57.74
1973    67.27
1974    78.57
1975    91.71
1976    106.7
1977    119.93
1978    135.84
1979    155.49
1980    178.29
1981    199.14
1982    215.75
1983    232.63
1984    260.41
1985    321.12
1986    361.95
1987    408.07
1988    464.38
1989    511.32
1990    551.36
1991    606.11
1992    691.74
1993    817.58
1994    941.95
1995    1040
1996    1100.08
1997    1219.09
1998    1319.3
1999    1452.94
;
proc gplot;
plot x*year;
plot dif1*year;
plot dif2*year;
symbol v=star c=red i=join;
run;

结果图：
原始序列图：
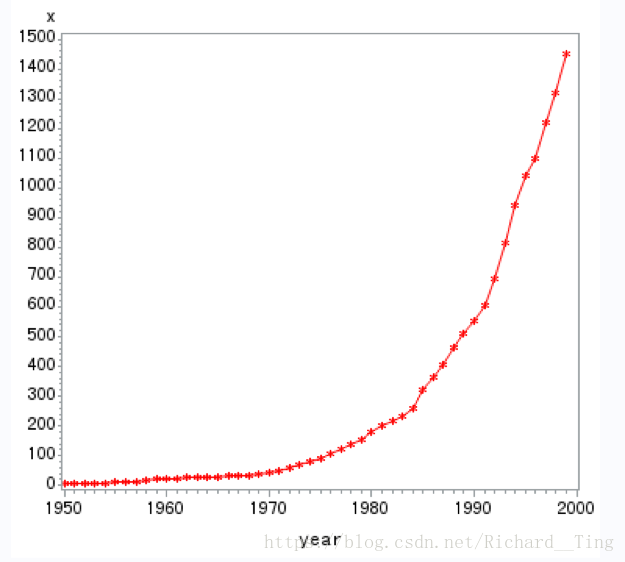
这里写图片描述
一阶差分：
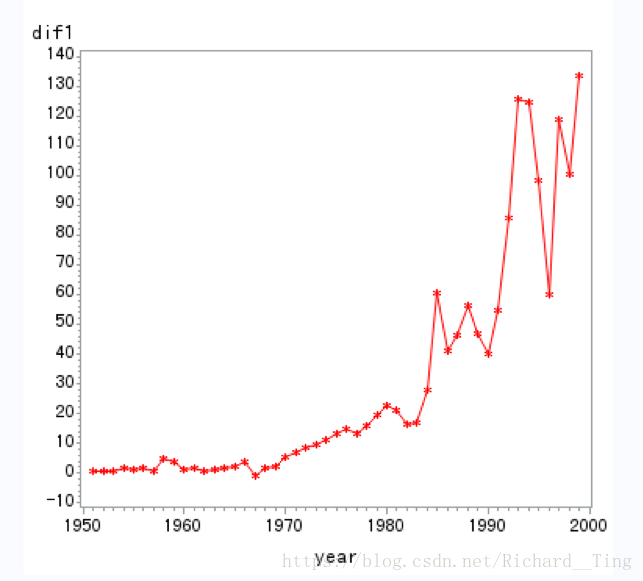
这里写图片描述
二阶差分：
这里写图片描述

  • 有着固定周期（看时序图和自相关图）-通常差分+步长
    例题3 差分运算提取1962年1月—1975年12月平均每头奶牛的月产奶量序列中的确定性信息。

代码：

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
data a;
input milk@@;
time=intnx('month','1jan1962'd,_n_-1);
format time year4.;
dif1=dif(milk);/*一阶差分*/
dif1_12=dif12(dif1);/*12步差分*/
cards;
589 561 640 656 727 697 640 599
568 577 553 582 600 566 653 673
742 716 660 617 583 587 565 598
628 618 688 705 770 736 678 639
604 611 594 634 658 622 709 722
782 756 702 653 615 621 602 635
677 635 736 755 811 798 735 697
661 667 645 688 713 667 762 784
837 817 767 722 681 687 660 698
717 696 775 796 858 826 783 740
701 706 677 711 734 690 785 805
871 845 801 764 725 723 690 734
750 707 807 824 886 859 819 783
740 747 711 751 804 756 860 878
942 913 869 834 790 800 763 800
826 799 890 900 961 935 894 855
809 810 766 805 821 773 883 898
957 924 881 837 784 791 760 802
828 778 889 902 969 947 908 867
815 812 773 813 834 782 892 903
966 937 896 858 817 827 797 843
;
proc gplot;
plot milk*time dif1*time dif1_12*time;
symbol v=diamond c=blue i=join;
run;

结果图：
原始序列图：
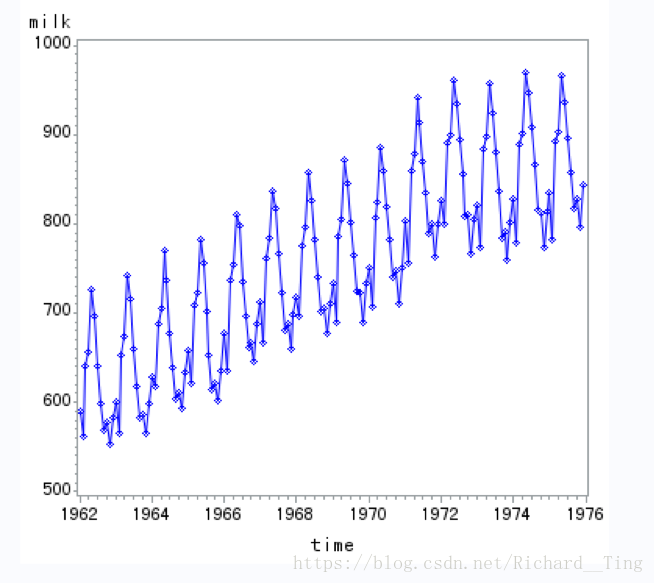
这里写图片描述
一阶差分：
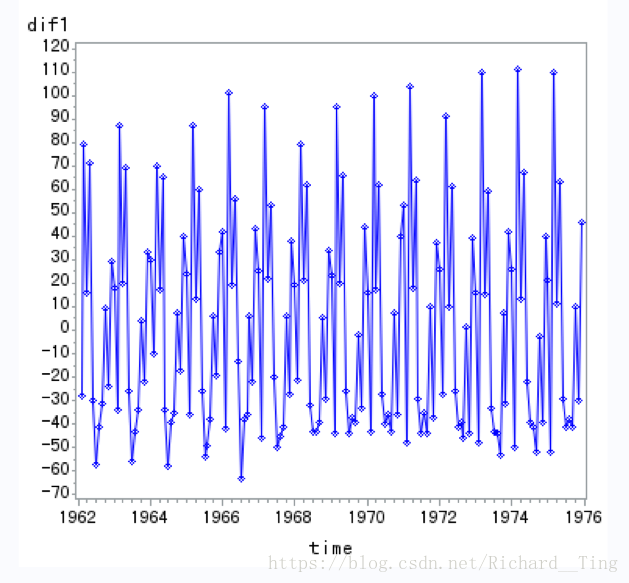
这里写图片描述
一阶12步差分：
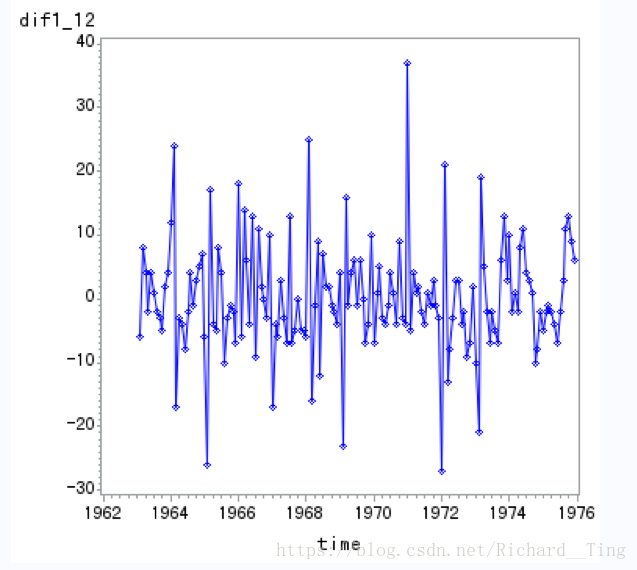
这里写图片描述

3.2 ARIMA模型的拟合

差分运算具有强大的信息提取能力，对差分运算后得到的平稳序列可以用 ARIMA 模拟进行拟合。

  • 模型结构
  • 模型建模
  • 疏稀疏模型
  • 季节模型
    • 简单季节模型
    • 乘积季节模型
3.2.1 模型结构

ARIMA模型使用场合：差分平稳序列拟合

模型表达式： ϕ(B)∇dxt=Θ(B)ϵt ϕ ( B ) ∇ d x t = Θ ( B ) ϵ t

3.2.2 模型建模

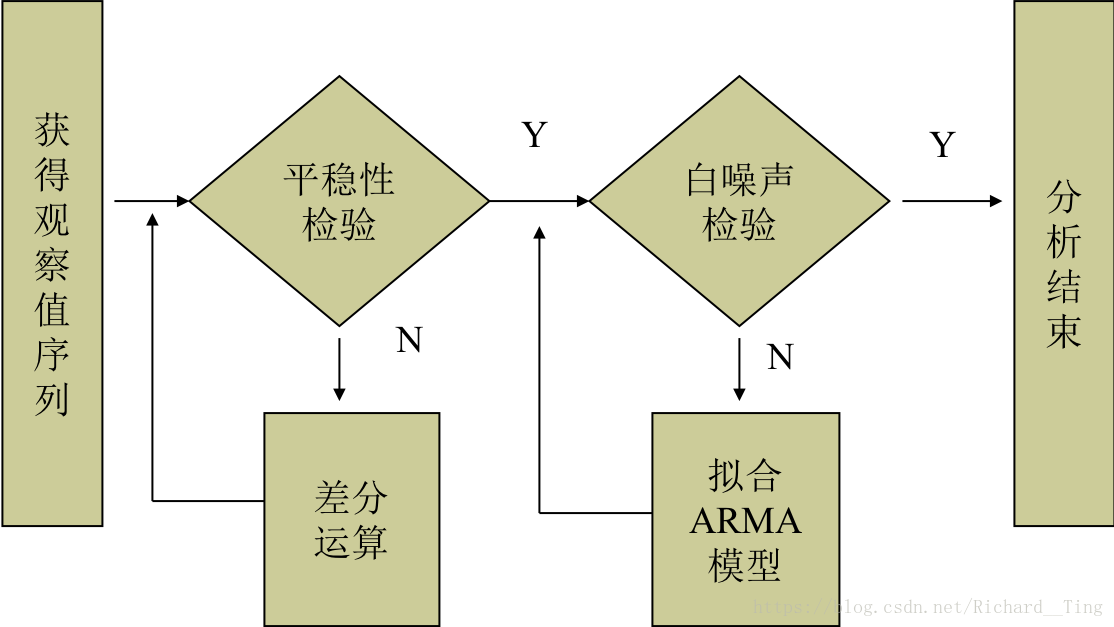
这里写图片描述

3.2.3 疏稀疏模型

ARIMA(p,d,q) A R I M A ( p , d , q ) 模型是指 d d 阶差分后自相关最高阶数为p，移动平均最高阶数为 q q 的模型，通常它包含p+q个独立的未知系数： ϕ1,...ϕp,θ1,...θq ϕ 1 , . . . ϕ p , θ 1 , . . . θ q 。
如果该模型中有部分自相关系数 ϕk,1≤k<q ϕ k , 1 ≤ k < q 或部分移动平滑系数 θj,1≤j<p θ j , 1 ≤ j < p 为零，即原模型中有部分系数省缺了，那么该模型称为疏系数模型。
可以简记作： ARIMA((p1,...,pm),d,(q1,...,qn)) A R I M A ( ( p 1 , . . . , p m ) , d , ( q 1 , . . . , q n ) )

3.2.4 季节模型
  • 简单季节模型： ∇D∇dxt=Φ(B)Θ(B)ϵt ∇ D ∇ d x t = Φ ( B ) Θ ( B ) ϵ t

建模方法类似平稳序列中的方法

例题1：拟合1962—1991年德国工人季度失业率序列。
代码：

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
goptions vsize=7cm hsize=10cm;
data a;
input x@@;
dif1=dif(x);
dif1_4=dif4(dif1);
time=intnx('quarter','1jan1962'd,_n_-1);
format time year4.;
cards;
1.1 0.5 0.4 0.7 1.6 0.6 0.5 0.7
1.3 0.6 0.5 0.7 1.2 0.5 0.4 0.6
0.9 0.5 0.5 1.1 2.9 2.1 1.7 2
2.7 1.3 0.9 1   1.6 0.6 0.5 0.7
1.1 0.5 0.5 0.6 1.2 0.7 0.7 1
1.5 1   0.9 1.1 1.5 1   1   1.6
2.6 2.1 2.3 3.6 5   4.5 4.5 4.9
5.7 4.3 4   4.4 5.2 4.3 4.2 4.5
5.2 4.1 3.9 4.1 4.8 3.5 3.4 3.5
4.2 3.4 3.6 4.3 5.5 4.8 5.4 6.5
8   7   7.4 8.5 10.1    8.9 8.8 9
10  8.7 8.8 8.9 10.4    8.9 8.9 9
10.2    8.6 8.4 8.4 9.9 8.5 8.6 8.7
9.8 8.6 8.4 8.2 8.8 7.6 7.5 7.6
8.1 7.1 6.9 6.6 6.8 6   6.2 6.2
;
proc gplot;
plot x*time=1 dif1*time=2 dif1_4*time=3;
symbol1 c=black i=join v=star;
symbol2 c=green i=join v=diamond;
symbol3 c=red i=join v=star;
/*step2
proc arima; 
identify var=x(1,4) minic p=(0:5) q=(0:5);
*/
/*step3
proc arima; 
identify var=x(1,4);
estimate p=1 method=ml;
*/
/*step4
proc arima; 
identify var=x(1,4);
estimate p=4 method=ml;
*/
/*step5
proc arima; 
identify var=x(1,4);
estimate p=(1 4) noint; /*why noint*/
*/
/*step6
proc arima; 
identify var=x(1,4);
estimate p=(1 4) noint; /*why noint*/
forecast lead=0 id=time out=out;
proc gplot data=out;
plot x*time=1 forecast*time=2 /overlay;
symbol1 c=black i=none v=star;
symbol2 c=red i=join v=none;
*/
run;

结果分析：
原始序列图
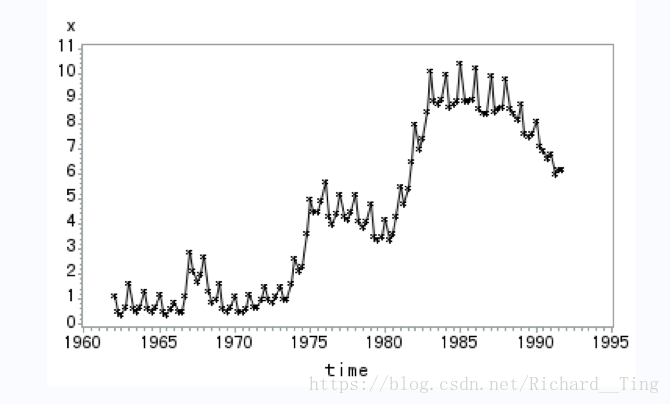
这里写图片描述
一阶差分序列图
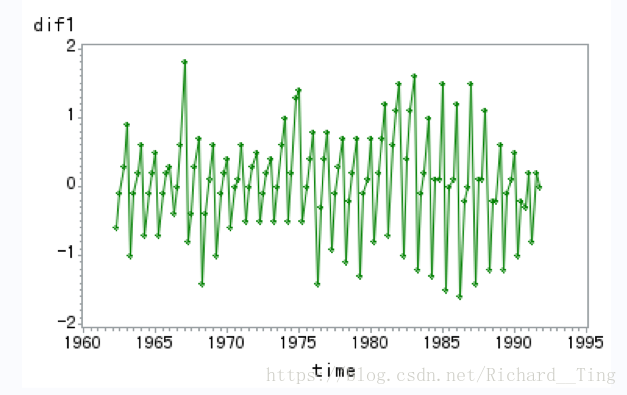
这里写图片描述
一阶12步差分序列（平稳）
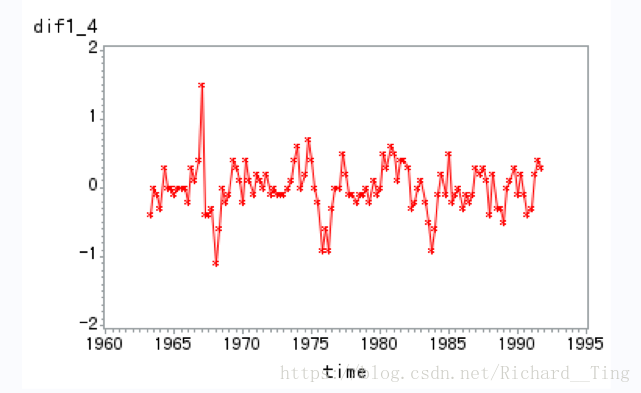
这里写图片描述
利用minic，发现两个可能的模型：ARIMA(1,(1,12),0)和ARIMA(1,(1,12),0)
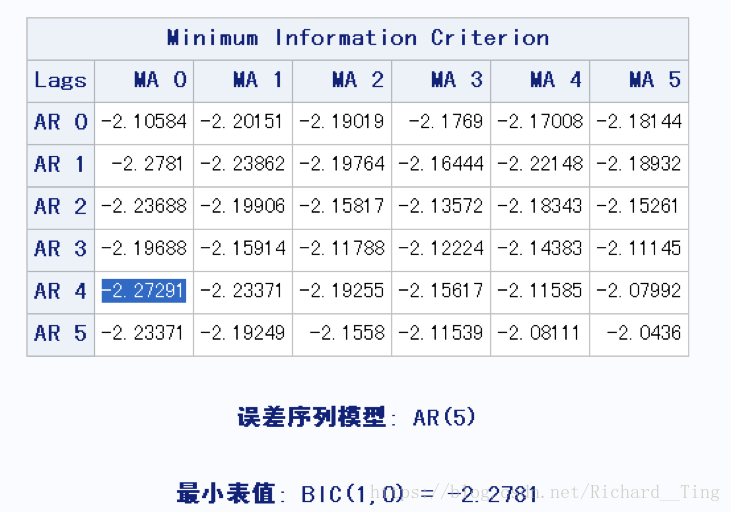
这里写图片描述
ARIMA(1,(1,12),0)先记录一下AIC值，记作x1=68
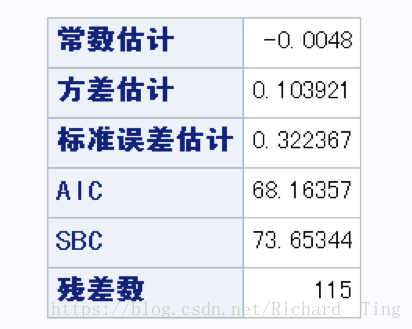
这里写图片描述
检验残差是否为白噪声，符合
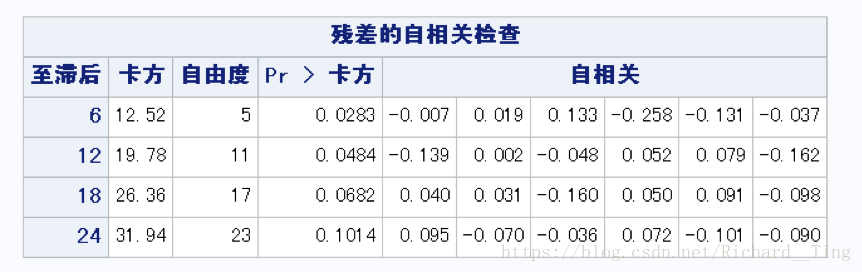
这里写图片描述
ARIMA(4,(1,12),0)记录另外一个AIC值，x2=61
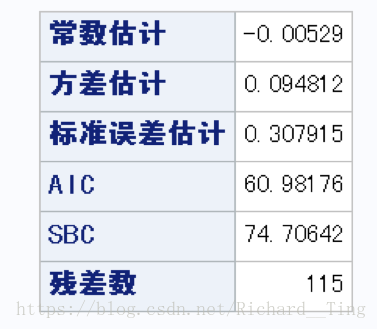
这里写图片描述
检验残差是否为白噪声，符合
这里写图片描述
不用说了，选择AIC值小的，这个模型非白噪声
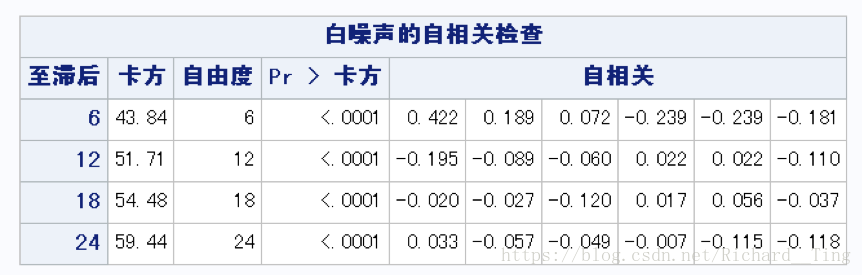
这里写图片描述
符合参数检验
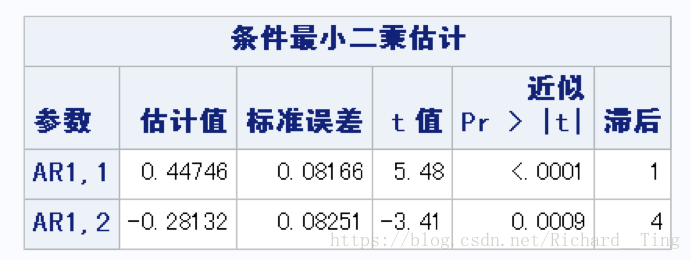这里写图片描述、
数学方程也可以写出来了。
这里写图片描述

最终模型： (1−B)(1−B4)xt=11−0.44746B+0.28132B4ϵt ( 1 − B ) ( 1 − B 4 ) x t = 1 1 − 0.44746 B + 0.28132 B 4 ϵ t

  • 乘积季节模型： ∇d∇DSxt=Θ(B)Θs(B)Φ(B)Φs(B)ϵt ∇ d ∇ S D x t = Θ ( B ) Θ s ( B ) Φ ( B ) Φ s ( B ) ϵ t

由于此模型推导很复杂，这里只给出一个例题代码。

例题2：拟合1948——1981年美国女性月度失业率序列。

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
data a;
input x@@;
dif1_12=dif12(dif(x));
time=intnx('month','1jan1948'd,_n_-1);
format time year4.;
cards;
446 650 592 561 491 592 604 635 580
510 553 554 628 708 629 724 820 865
1007 1025 955 889 965 878 1103 1092 978
823 827 928 838 720 756 658 838 684
779 754 794 681 658 644 622 588 720
670 746 616 646 678 552 560 578 514
541 576 522 530 564 442 520 484 538
454 404 424 432 458 556 506 633 708
1013    1031    1101    1061    1048    1005    987 1006    1075
854 1008    777 982 894 795 799 781 776
761 839 842 811 843 753 848 756 848
828 857 838 986 847 801 739 865 767
941 846 768 709 798 831 833 798 806
771 951 799 1156    1332    1276    1373    1325    1326
1314    1343    1225    1133    1075    1023    1266    1237    1180
1046    1010    1010    1046    985 971 1037    1026    947
1097    1018    1054    978 955 1067    1132    1092    1019
1110    1262    1174    1391    1533    1479    1411    1370    1486
1451    1309    1316    1319    1233    1113    1363    1245    1205
1084    1048    1131    1138    1271    1244    1139    1205    1030
1300    1319    1198    1147    1140    1216    1200    1271    1254
1203    1272    1073    1375    1400    1322    1214    1096    1198
1132    1193    1163    1120    1164    966 1154    1306    1123
1033    940 1151    1013    1105    1011    963 1040    838
1012    963 888 840 880 939 868 1001    956
966 896 843 1180    1103    1044    972 897 1103
1056    1055    1287    1231    1076    929 1105    1127    988
903 845 1020    994 1036    1050    977 956 818
1031    1061    964 967 867 1058    987 1119    1202
1097    994 840 1086    1238    1264    1171    1206    1303
1393    1463    1601    1495    1561    1404    1705    1739    1667
1599    1516    1625    1629    1809    1831    1665    1659    1457
1707    1607    1616    1522    1585    1657    1717    1789    1814
1698    1481    1330    1646    1596    1496    1386    1302    1524
1547    1632    1668    1421    1475    1396    1706    1715    1586
1477    1500    1648    1745    1856    2067    1856    2104    2061
2809    2783    2748    2642    2628    2714    2699    2776    2795
2673    2558    2394    2784    2751    2521    2372    2202    2469
2686    2815    2831    2661    2590    2383    2670    2771    2628
2381    2224    2556    2512    2690    2726    2493    2544    2232
2494    2315    2217    2100    2116    2319    2491    2432    2470
2191    2241    2117    2370    2392    2255    2077    2047    2255
2233    2539    2394    2341    2231    2171    2487    2449    2300
2387    2474    2667    2791    2904    2737    2849    2723    2613
2950    2825    2717    2593    2703    2836    2938    2975    3064
3092    3063    2991                        

;
proc gplot;
plot x*time dif1_12*time;
symbol c=black i=join v=none;
proc arima;
identify var=x(1,12);
estimate p=1 q=(1)(12) noint;
forecast lead=0 id=time out=out;
proc gplot data=out;
plot x*time=1 forecast*time=2 /overlay;
symbol1 c=black i=none v=dot;
symbol2 c=red i=join v=none;
run;

总结

  1. 非平稳序列化为平稳序列，查看是否白噪声。
  2. 若不是白噪声，继续检验。
  3. 利用minic确定稀疏模型。
  4. 查看残差是否为白噪声。
  5. 若不是，模型符合，继续检验系数的显著性。
  6. 最后得到模型。

最后

以上就是悲凉康乃馨最近收集整理的关于2.3-非平稳时间序列分析总结的全部内容，更多相关2内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(80)

相关文章

Tips_SystemC
Tips_SystemC
SkyEye硬件模拟平台，第三部分: 硬件仿真实现之五
SkyEye硬件模拟平台，第三部分: 硬件仿真实现之五
System Design with SystemC 的学习笔记
System Design with SystemC 的学习笔记
systemC的仿真平台书写
systemC的仿真平台书写
2.3-非平稳时间序列分析总结
2.3-非平稳时间序列分析总结
SystemC和Skyeye的集成
SystemC和Skyeye的集成
SystemC的运行阶段
SystemC的运行阶段
HDL4SE：软件工程师学习Verilog语言（十二）12 SystemC
HDL4SE：软件工程师学习Verilog语言（十二）12 SystemC

评论列表共有 0 条评论

立即
投稿
返回
顶部